ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Pallavi J 1, Kavitha T M 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Electronic Product Code or EPC Global class-I Generation-I and Generation-II are popular and globally accepted standard specification which enables the use of password protection for accessing the data stored in the memory of a RFID tag. Use of password gives one of the ultimate securities for the RFID system but these are not immune to ‘hacking’. Hackers are adopting advance technologies like side attack, power analysis to detect data password. But in many cases it is very much important that data must be secured enough. In this paper, we propose a data security system integrated with this protocol based on RSA algorithm. The RSA system is widely employed in networking applications and achieves good performance and high security. We have implemented the protocol in VERILOG.A synthesizable module is presented here in this article. System efficiency is evaluated according to the implementation.
Keywords |
| EPC Gen-2, RFID, RSA, VERILOG, RTL schematic, Simulation, Synthesis report. |
INTRODUCTION |
| The global standard EPC Gen-2 protocol is the advanced version of EPC Gen-1 protocol. Some disadvantages and shortcomings of EPC Class 1 Gen1 overcome in the revised EPC Gen-2 protocol, which uses ALOHA based random anti-collision protocol called Q protocol (Q algorithm).It is of frame slotted ALOHA based probabilistic algorithm for tag anti-collision protocol with dynamic frame length. |
| VLSI implementations of algorithms are very important to achieve desired reliability, performance, low cost and high speed production. There are three possible types of slots; empty slot, when there is no tag to reply. Collided slot, when more than one tag to respond and the successful slot, when there is only one tag to respond and exchange information. The three conditions are depicted in Figure 1 with Q value 2. Tags are asked to choose slot number SN within the range 0 ≤ SN ≤ (22-1). So, the tags can choose 0, 1, 2 and 3 as their SN. But, if no tag is chosen, SN = 0, then the slot will be an empty and no tag will reply. When more than one tag choose SN = 0, it results a collided slot and reader modified its Q value and ask the tags to choose new SN. Successful slot, when only one tag responds to the Reader with SN = 0 and generates the 16 bit number RN16 and transmit. |
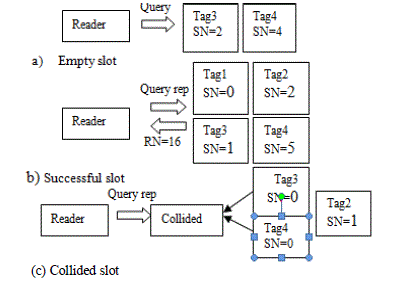 |
| (c) Collided slot |
| Fig1: Empty, successful and collided slots. |
| EPC Class 1 Gen1 and EPC Class 1 Gen2 protocols are ratified as the International standard anti-collision protocol. But in EPC code data are not encrypted, rather covered by more pseudo-random number or data. Hence attackers or hackers can decode the data in several ways. So, password security does not provide the ultimate security for important data. It is possible to discover the details personal data if anybody has the knowledge of EPC references. Side channel attacks are executed by watching the power consumption or variations of the energy output of the devices. Important data or personal information especially sensitive personal data will need an adequate level of encryption to safeguard the data. Hence instead of PCA which is used for securing the data in the existing system we are using a cryptography method in order to give high level security to the data or password. We have used RS algorithm to generate a secret code using a secret key within the EPC tag. We have designed the secret code generator and the processor both for the reader and the tag in VERILOG code. Hence an unauthorized Reader will not be able to read the data unless the key is available. |
RELATED WORK |
| [1] With reference to the paper Analysis of Tree Algorithms for RFID Arbitration the nee Search (or splitting) method introduced by Capetanakis for use in conventional multi-access systems can also be applied to RFID arbitration. This paper performs a transient analysis of this, and related methods. Radio Frequency Identification (RFID) systems have emerged as a viable and affordable alternative for tagging and/or labelling small to large quantities of items. The arbitration problem is that of identifying all ‘tags’ present in the current environment (i.e. reading the labels). This is a multi-access communication problem in which contention for the communication medium is transient in nature. Important measures of performance include the time required to identify the tags, and the power consumed by the tags. The first of these is proportional to the number of time slots needed to complete the arbitration process, and the second is proportional to the total number of times the tags are required to transmit during this process. We analyze a family of nee Search algorithms with respect to these two measures. Previous analysis on the average number of time slots reveals a linear dependence on the number of tags. We extend this work by developing expressions for the decomposition of these slots into three basic types: zero, one and multiple reply slots. Original expressions are also developed for the total number of tag replies. |
| [2]With the analysis of the paper A Programmable Hardware Cellular Automaton: Example of Data Flow Transformation we present an IP-core called PHCA for Programmable Hardware Cellular Automaton (CA). PHCA is a hardware implementation of a general purpose cellular automaton entirely programmable. The heart of this structure is a PE array with reconfigurable side links allowing implementing a 2-D CA or a 1-D CA. As an illustration of a PHCA program we present the implementation of a symmetric cryptography algorithm called ISEA for Ising Spin Encryption Algorithm. Indeed ISEA is based on a 2-D Ising spin lattice presenting random series of disordered spin configurations. The main idea of ISEA is to use the disordered spin configurations to encrypt data. Cellular automata were originally introduced by von Neumann for studying self-reproduction in biological systems. Then they have been used for language recognition and modeling of physical systems. The mathematical properties of cellular automata were also studied. Nowadays the concept of quantum cellular automata is defined everywhere. [3]According to the paper Query Tree-Based Reservation for Efficient RFID Tag Anti-Collision Since the tree based RFID tag anti-collision protocol achieves 100% read rate, and the slotted ALOHA based tag anti-collision protocol allows simple implementation and good performance in small amount of tags, we consider how to take the advantages of each algorithm. This paper presents query tree based reservation for efficient RFID tag anti-collision. According to the simulation results, the proposed protocol requires less time consumption for tag identification than the present tag anti-collision protocols implemented in EPC Class 0, Class 1, and Class 1 Gen. 2. FID systems are coming the most promising technologies used for contactless object identification. One of the research areas in RFID systems is a tag anti-collision protocol; how to reduce identification time with a given number of tags in the field of an RFID reader. For fast tag identification, anti-collision protocols, which reduce the frequency of collisions occurred and identify tags independent of occurring collisions, are required. Moreover, tag anti-collision protocols are more important than reader anticollision protocols because of the incompetence of tags in low-cost passive RFID systems. There are two types of tag anti-collision protocols for RFID systems: deterministic methods and probabilistic methods The deterministic methods are tree based protocols The tree based protocols keep splitting the group of colliding tags into two subgroups until all tags are identified. The probabilistic methods are based on slotted ALOHA. The slotted ALOHA based protocols reduce the probability of occurring tag collisions how tags respond at the different time. This paper considers how to improve the performance of the RFID tag anti-collision protocol by applying the characteristics of EPC Class 1 Gen2 protocol to the query tree algorithm. |
SYSTEM AND DESIGN |
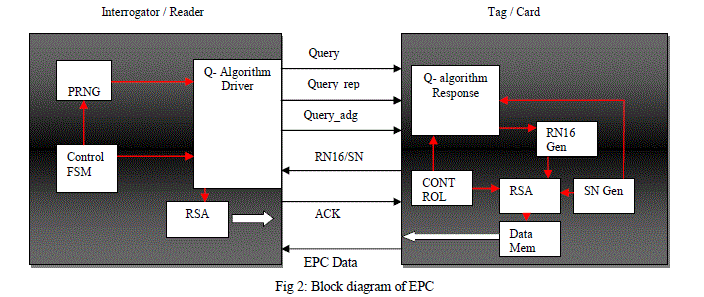 |
| As soon reset is released the FSM triggers the Q algorithm block of the interrogator module to start the communication with reader block. Parallely it also enables the PRNG block to generate the SN numbers to be able to compare the SN received from reader module. Once the Tag or reader is identified the RSA module will be enabled by control FSM, the RSA module starts decoding the received data based on RSA decryption algorithms. The reader module will also simultaneously starts the control FSM as soon reset is released. The control FSM triggers the Q algorithm response block to respond the interrogator also it triggers the SN Gen module to generate the Random SN number which will be transmitted to interrogator as soon tag is identified, FSM triggers the RSA block, RSA block on request from interrogator reads the data from the Data Memory and then Encrypts it based on the RSA algorithm with private and Public key and then it will be transmitted on the data line. |
| PRNG MODULE :The architecture of the PRNG block is given in Fig 3. For the whole circuit, there are five input signals. Those are the input signal to be shifted into the serial-to-parallel shift register as the input seed for RNG to generate the random numbers (Inbit), the clock pulse for PRNG and shift register (Clk), the reset and activate signal for PRNG (Reset), the reset signal for shift register (Reset_shift), and the enable signal for the register (Enable_reg). The output pins are the 16-bit random number output signal (Outbit) and the read enable signal for the next stage (Enable_read). |
| The PRNG circuit consists primarily of three blocks of circuitries: a 16-bit Serial-to-Parallel shift register, a 16-bit register, and a PRNG module which takes in an input seed of 16-bit width and generates a random 16-bit number using the Park-Miller Algorithm. The serial-to-parallel shift-in register is used to set the initial states of the 16bit RNG. It shifts in the single bit inputs “InbitâÃâ¬ÃŸ to form a 16-bit input seed under the control of the “Reset_shiftâÃâ¬ÃŸ signal. After initialization, at every rising edge of the “ClkâÃâ¬ÃŸ signal, if the “Enable_regâÃâ¬ÃŸ signal is high, the 16 bit register will take in the value of the outputs of the shift register and the PRNG module will update its state according to the output of the multiplexer. |
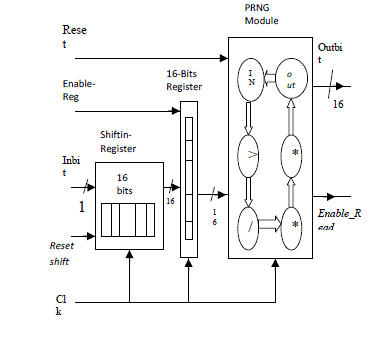 |
| RSA : Our proposed method uses the RSA algorithm compared to PCA method proposed in referred papers. Below are details of RSA algorithm and implementation. The entire RSA cryptosystem is divided in to three parts: key generation, encryption and decryption. The design of each module required to build the RSA cryptosystem is described in this chapter. The implementation block diagram of RSA Cryptosystem is shown in fig 4. |
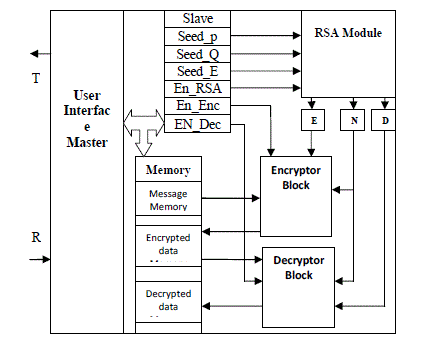 |
| As shown in the fig 4 seed values required for the RSA module and En_RSA, En_Enc, En_Enc are stored in the slave register. RSA module generates public key “EâÃâ¬ÃŸ, private key “DâÃâ¬ÃŸ and the modulus “NâÃâ¬ÃŸ by using random number generator, prime number detector, Booth multiplier and Extended Euclidean Algorithm. The implementation block diagram of the RSA module is shown in fig 4. When the En_enc signal is toggled Encryptor takes the message, private key EâÃâ¬ÃŸ, modulus NâÃâ¬ÃŸ and generates cipher text which is stored in the Encrypted data memory. When the En_dec signal is toggled Decryptor takes the cipher text, public key “EâÃâ¬ÃŸ, modulus “NâÃâ¬ÃŸ and generates decrypted data which is stored in the decrypted data memory. These are connected to the User Interface Master in which data are received and transmitted to the user. |
| Encryption : A critical requirement for the proper functioning of the RSA algorithm is that the message M must be represented as an integer in the range [0, n-1] (where n is, as usual, the RSA modulus). Our application converts text messages to integers by using a simple mapping of every character to its ASCII code and encrypts two characters at a time. For an RSA encryption scheme with the modulus size of 1024 bits, we have seen that about 100characters can be encrypted at once. Lesser number of characters cause encryption and (especially) decryption to take significantly longer, whereas higher number of characters often violate the condition that the message M must lie in the interval [0, n-1]. The encryption works using the public key (e, n). For any input message “m”, the encrypted message “c” would be calculated is using: |
| C=Me mod n In above calculation “e” can be a very large number. In this project, “e” is a sixteen bit number. If the Me is calculated first them for a very small value of “e” then resultant number can be very large and cannot be stored in the memory. The message “M” will be sent multiplier, at first multiplicand and multiplier will be same as message “M” then the product is divided by value of “N” then the modulus of it will be sent back to multiplier if the counter value is less than the “E” value or else the modulus is considered as encrypted data. Once counter value reaches to the value of “E” it also toggles a “done” signal to indicate that the encryption process is over. |
| Decryption: As the user chooses to decrypt an encrypted file, the decryption part is invoked. The operation of this routine is quite straightforward. From the file to decrypt (the path to which is input from the user), the function processes each encrypted integer. It does so by computing the value of cd mod n and stores the decrypted part. Of course, the values of d and n are read in earlier. Here M however contains the integer representation of the information i.e. it is a string of numbers where each 2 character sequence signifies the ASCII code of a particular character. An inverse mapping to the relevant character is carried out and the information, now as was in the original file is displayed on the standard output. The decryption process is over once all the integers (cipher text) in the encrypted file are processed and decrypted in the described manner. |
| M=Cd mod n |
| In above calculation “d” can be a very large number. In this project, “d” is a sixteen bit number. If the cd is calculated first them for a very small value of “d” then resultant number can be very large and cannot be stored in the memory decryption. |
| The encrypted data “C” will be sent multiplier, at first multiplicand and multiplier will be same as encrypted data “C” then the product is divided by value of “N” then the modulus of it will be sent back to multiplier if the counter value is less than the “D” value or else the modulus is considered as decrypted data. Once counter value reaches to the value of “D” it also toggles a “done” signal to indicate that the decryption process is over. |
SIMULATION RESULT FOR THE MODULES |
| Simulation results of (a) Control FSM (b) Data memory (c) q_algorithm (d) RNG (e) RSA (f) Top module |
 |
| (a) It has 7 states where idle, send_querry, Rx_sn, send_querry_rep,querry_adj, sec_det, tag found are inputs and cs(current state),ns(next states) are outputs. Here clk and reset are global signals which are high for all states. |
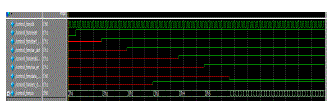 |
| (b) Here clk and reset are the global signals which will be high always. It has 6 states where idle, start, tag_det, ENC_det_rx, RSA_en, data_rxd is inputs and cs (current state) is the output. All states will be enabled when it is high. If it is not high it goes back to the idle state and waits for the present state to become high. |
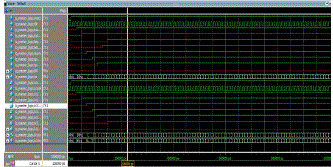 |
| (c) Data memory is used to store the data which is designed under the TAG module. It stores the data up to 1024 bits of data which supports the Spartan 6 fpga kit. Here clk, data_in_bus, data_out_bus, address_bus, chip_select, read_enable and write_enable are the inputs and 32 bit memory is the output. Here clk is high for the entire process |
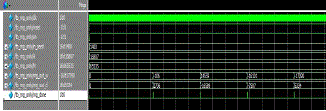 |
| (d) Random number is generated using a park miller algorithm which i s based on the linear form. In the above simulation result shown clk, reset and en(enable) signals are high throughout the design. In_seeed is the input given of 16 bit, A is a constant which is the input signal and M is the message signal is always a 16 bit random number |
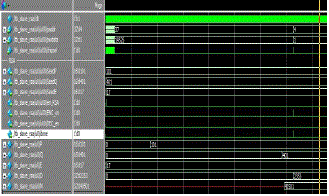 |
| (e) Here clk is a global signal.paddr, pwdata and chipsel are the input programmable busses. Seed p, q,e are the inputs to the rsa module where p,q,e are the inputs to the seed p,q,e respectively. Dec_en and enc_en are the toggle signals to enable encryption and decryption process. D is the decrypted key and N is the encrypted key generated as outputs from the rsa module. |
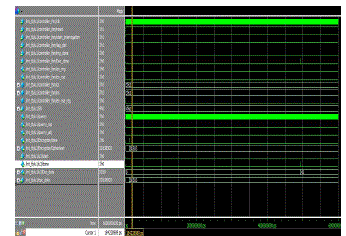 |
| (f) Clk and reset is high throughout the process. Once reset is high reader will start interrogation with the tag and when tag is detected tag_det will become high and send an acknowledgement rng_done back to reader when it is high. Then dec_done signal is enabled and the decrypted data is received at the output. The cipher text generated is the random number generated for the encrypted message output signal |
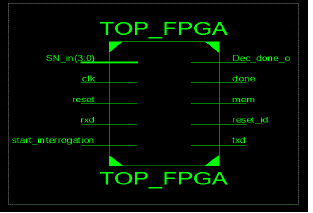 |
| Above figure shows the RTL of the top module of EPC gen2 system design. It consists of clk, reset, rxd, mem, start_interrogation as input signals and dec_done, sn_in and txd as output. |
CONCLUSION |
| In this paper we have designed and implemented the EPC Gen-2 protocol in VERILOG code to get better performance, improved speed and efficiency and security. The design is targeting the Xilinx FPGA device, this leads to real time environment verification of the system.VLSI Design of protocol is performed to achieve high speed, minimum hardware and enhanced system efficiency with highly secured data transfer to authenticated reader. The RSA architecture generates all the possible random numbers for the given 16 bit input and stores it in a memory. Prime numbers from the generated random numbers were identified and stored in a memory. The first two prime numbers stored in the memory is selected for encryption. Also the generation stops as soon as the system detects two prime numbers. The efficiency will be increased by a considerable amount in terms of the above mentioned parameters. |
References |
|