ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R. Ganesan 1, S. Vignesh 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
DC- DC converter plays an important role in power conversion. They are used in many applications like computer power supplies, switching mode regulators etc. Control action of buck converters involves maintaining constant output voltage in the presence of change in load and change in supply voltage conditions. Traditional controllers like PID controllers have limitation in control action whenever the changes are rapid in nature. Fuzzy controllers described by linguistic variables can be employed for buck converter output voltage control. Fuzzy controller can be used as stand alone or in conjunction with PI controller for buck converter output control. In this paper design and simulation using MATLAB/SIMULINK of buck converter output voltage using fuzzy logic control is presented. Simulation results are presented to prove that the steady state deviations of fuzzy PI controller are minimum
Keywords |
| Buck converter, PI control, fuzzy control, MATLAB-SIMULINK. |
INTRODUCTION |
| The buck converter is a dc-dc converter that is used for stepping down dc voltage level. They are used for mother board supplies in personal computers. They use power electronics switches that can be made on or off to maintain a specified output voltage level. The essence of control action is to maintain desired voltage level in the presence of load side disturbances (load change) and supply side disturbances (input voltage variations). Traditional PID control is employed for buck converter control action. But the control action is subject to component ageing, poor transient response, long settling time and instability in the presence of severe disturbances. Fuzzy controllers are defined by linguistic variables. As such their control action is independent of component ageing. Earlier methods centred around isolation of state variables for feedback control [1]. Uran et al. proposed feedback loop control [2]. Linear Quadratic Controller (LQR) was proposed to improve control action [3]-[4]. Lee C. C. has dwelled upon the application of fuzzy logic control to many control actions [5]. Fuzzy control being a non linear control is independent of measurement and noise error. In addition fuzzy control is adaptable by redefining membership fuctions. This paper is organized as follows: section 2 describes buck converter circuit and its modeling, section 3 describes fuzzy logic controllers, section 4 describes proposed buck converter control section 5 simulation results and section 6 conclusions. |
BUCK CONVERTER CIRCUIT |
| A buck converter is shown in Fig. 1 where the power electronics circuit S is controlled by duty cycle ratio as dictated by output voltage requirement. The buck converter is so called as its output voltage is always lower than input voltage [6]. |
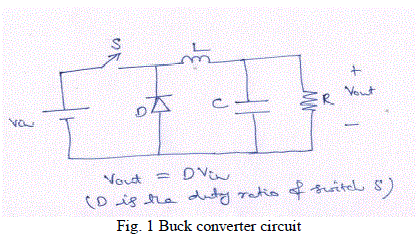 |
| There are three states of the circuit: |
| (i) Switch S on, Diode D off; |
| (ii) Switch S off, Diode D on; |
| (iii) Switch S off, Diode D off. |
| Switch S is controlled by pulse width modulation (PWM) technique. In this, a saw tooth voltage is compared with a fixed dc voltage and if saw tooth voltage is lower than the fixed dc voltage then switch S is closed or else switch S is open. |
| The equations for buck converter are presented as below: [7] |
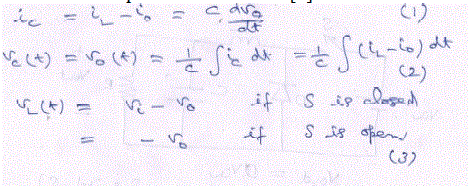 |
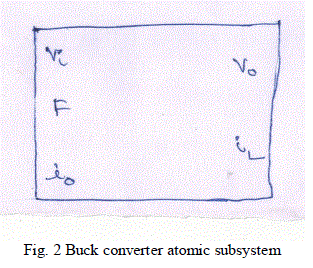
| Entire buck converter is modeled as Matlab Simulink block with Vi,Io, F as input variables and Vo, IL as output variables as shown in Fig. 2. F is the gate signal. |
 |
FUZZY LOGIC CONTROLLER |
| In 1965, Zadeh proposed fuzzy logic. A simple block diagram of fuzzy controller is shown in Fig. 3. |
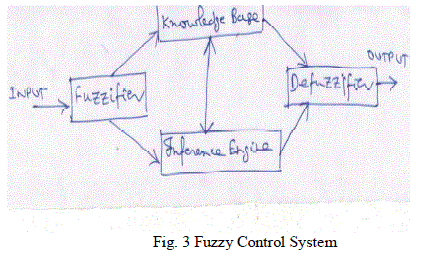 |
| Four major units of fuzzy controller are: fuzzification block, fuzzy knowledge base, fuzzy inference engine and defuzzification block [8]. Fuzzification block measures, scales and converts the input into a set of linguistic variables. Fuzzy knowledge base contain fuzzy rule which are in the form of IF-----THEN linguistic statements. Fuzzy inference engine is an important block by which fuzzy logic controller mimic human intelligence in decision making. Defuzzification block converts fuzzy control actions into crisp signals. |
CONTROLLER FOR BUCK CONVERTER |
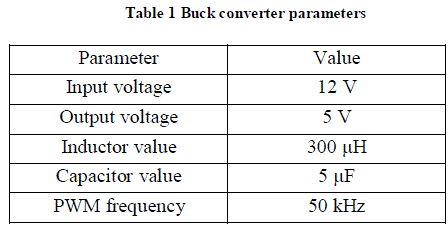
| The buck converter parameters are given in Table 1. |
 |
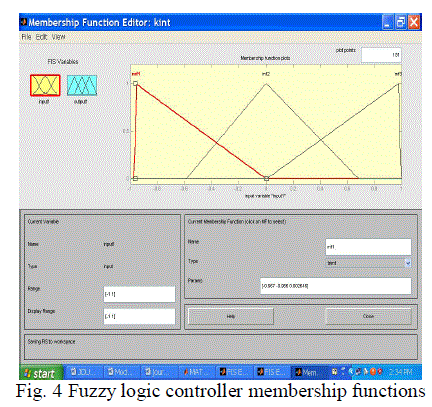
| The goal of the controller can be stated as follows: To maintain the output voltage constant at 5V in spite of load changes. For the buck converter initially PI controller is used. The design of PI controller is done as follows: Adjust the value of Kp till the desired output is obtained ignoring any offset and adjust Ki to reduce any offset error. A value of Kp=100 and Ki=50 was found to be sufficient.Now PI controller parameters are finetuned with fuzzy logic controller. Error input scaled to -1 to +1 is used as input t fuzzy control block. The input and output membership functions mf1, mf2 and mf3 for Kp and Ki block are presented in Fig. 4. For example the error from -1 to 0 is classified as mf1 with membership value as shown in Fig. 4.The error is presented to fuzzy control block and then multiplied with Kp and Ki value of PI controller in the modified fuzzy PI controller to generate modulating wave of PWM block [9]. The ultimate switching signals are generated by PWM. |
 |
| The rule base is presented as follows: |
| If input is mf1 then output is mf1 |
| If input is mf2 then output is mf2 |
| If input is mf3 then output is mf3 |
SIMULATION RESULTS |
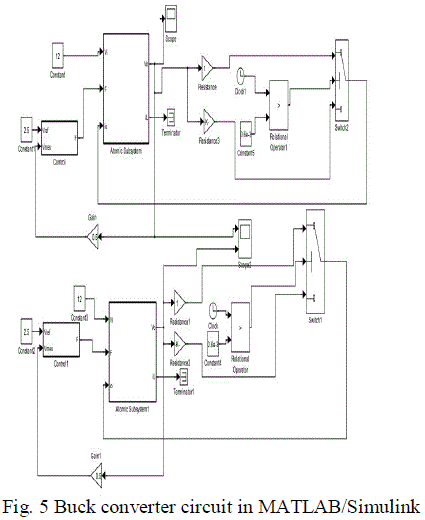
| Matlab/Simulink circuit for the buck converter circuit is presented in Fig. 5. |
 |
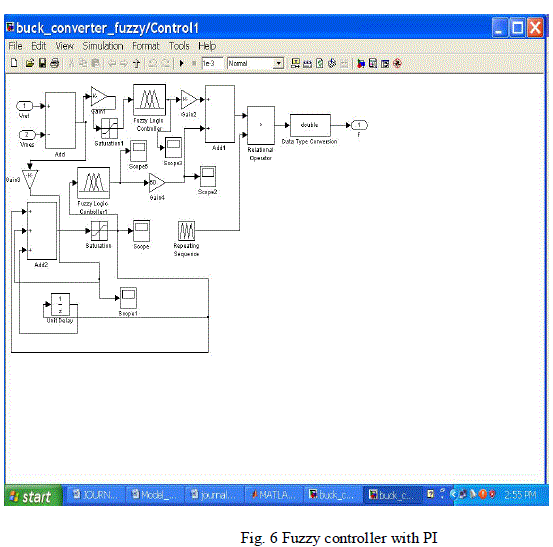
| The buck converter block is implemented as separate subsystem. The error is applied to P-I controller. The output of PI controller is given to PWM block. In PWM block the error signal is compared with triangular wave of switching frequency to generate PWM signals. The fuzzy controller along with PI is shown in Fig. 6. In fuzzy controller block, the error signal is applied first to membership block. The output of the fuzzy block is given to PI controller. PI controller output is given to PWM block to generate switching signals. |
 |
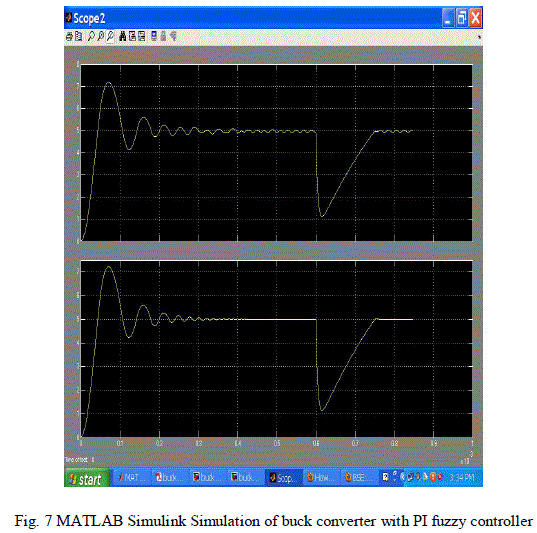
| In the simulation circuit, at 0.6ms the load was changed from R= 1ohms to R=8 ohms. Still the buck converter was able to maintain its output voltage. Fig. 7 presents the simulation results. The upper graph shows the simulation of the buck converter with PI controller and the lower graphs shows simulation with fuzzy controller. From the figure, we can infer that fuzzy controller is able to maintain its output voltage at 5V with minimal steady state deviation than PI controller. |
| From the simulation we can infer that a fuzzy PI controller can maintain tight output voltage keeping steady state error in output voltage to minimum and hence fuzzy PI controller presents a good alternative to be used with conventional PI controllers. Moreover as the control circuit uses linguistic variables, it is not prone to ageing like conventional PI circuits. Additional advantage can be adaptability by simply changing the fuzzy knowledge base. |
 |
Conclusion |
| In this research paper buck converter controller using PI controller was studied first. Application of fuzzy logic to output voltage error and fuzzy inference of output voltage error was applied to conventional PI block gain Kp and Ki. This greatly improved the steady state error of buck converter output voltage. Finally the simulation results of both converters were compared. From the simulation results it is concluded that application of fuzzy logic to PI controller is an option when tight steady state deviations are needed as in the case of PC power supply. |
ACKNOWLEDGMENT |
| First author wishes to thank his friend Dr. P.S. Srinivasan, Former Dean/EEE, SASTRA University for all his help. |
References |
|