Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Design of a Novel Intelligent Damping Controller for UPFC in Power System Connected Offshore Wind Power Applications

Whei-Min Lin1, Kai-Hung Lu2
  1. PhD. Student, Department of Electrical Engineering, National Sun Yat-Sen University, Kaohsiung, Taiwan
  2. Professor, Department of Electrical Engineering, National Sun Yat-Sen University, Kaohsiung, Taiwan
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper proposes a unified power flow controller (UPFC)-based oscillation damping controller for use with a permanent magnet synchronous generator (PMSG)-based offshore wave farm (OWF). A novel intelligent damping controller (NIDC) was used to increase the stability of power control and improve the performance, where the proposed NIDC consists of the adaptive critic network, the Functional Link based Elman Neural Network (FLENN), and PID linear damping controller. The UPFC is used with the NIDC to OWF, which is connected to a single-machine infinite-bus to improve system stability. The PID damping controller is analysis of complex eigenvalues based on a theory of modal control. The node connecting weights of the FLENN and critic network are trained online. The proposed NIDC can be used to achieve better damping characteristics. The internal power fluctuations in the power system can also be effectively alleviated under variable wind power generation

Keywords
unified power flow controller (UPFC), Functional Link based Elman Neural Network (FLENN), offshore wave farm (OWF), PM synchronous generators (PMSG)

INTRODUCTION
Wind energy systems are attracting considerable attention as clean and safe sources of renewable power. Among the types of generator used for wind turbines, technical developments have moved from fixed-speed to variable-speed designs [1]. In recent years some small-scale offshore wind farms (OWFs) have been evaluated, while a number of large-scale OWFs have been constructed and are now in commercial operation. Researchers have examined induction generators with wound-rotor or cage-type rotors [2], [3], but in recent years there has been increasing interest in Permanent Magnet Synchronous Generators (PMSG). Such generators are attractive due to their compact structure, high air–gap flux density, high power density, high torque-to-inertia ratio, and high torque capability [4]. When OWFs deliver a large amount of electric power to power grids, the inherent power fluctuations that occur can have adverse impacts on the power quality of the systems to which they are connected. This paper thus proposes the use of a unified power flow controller (UPFC) in order to reduce the power fluctuations of large-scale grid-connected wind farms.
The UPFC proposed by Dr. Gyugyiin 1991, is the most flexible and powerful Flexible AC Transmission Systems (FACTS) device [5]-[8], which can provide an effective means to control the power flow, voltage and damping, and thus improve the transient stability of a power network. In the control of a UPFC series branch, both the active and reactive power flows in the transmission line are influenced through the series injected voltage as well as its phase angle [7], [8]. A fixed-parameter controller with classical control may thus not be effective for a UPFC [8], [9]. In such cases a flexible controller may be required, such as one based on neural networks [6], PSO [10] and robust control methodologies [11], in order to cope with system uncertainties and enhance the damping performance of a UPFC.
The Elman neural network (ENN) is a partially recurrent network model that was first proposed in 1990 [12]. The ENN is better than a static feed-forward network, and thus is widely applied with dynamic systems, although its convergence and training speed are usually very slow, and this it is not suitable for complex systems. In order to improve the ability to identify complex dynamic systems, a functional-link neural network (FLNN) is adopted in this paper to improve the performance of the ENN. This improved performance is because the input variables are linearly independent trigonometric basis functions which are used for a functional expansion of the FLNN in the extended space for classification. Moreover, the FLNN can capture the nonlinearly input–output relationships among a suitable set of polynomial inputs, since the high-order effects are incorporated in the input variables into higher dimensions of the input space. The FLNN can thus effectively approximate a nonlinear function [13], and so it is suitable to be applied in complex power system applications, such as the one examined in this work.
This paper proposed the design of a novel intelligent damping controller (NIDC) consists of a PID linear controller, functional link-based Elman Neural Network (FLENN) and critic network for a UPFC damping controller. The PID linear controller is analysis of complex eigenvalues based on a theory of modal control. An FLENN is unlike conventional controllers, the performances of which degrade for such changes and require retuning to produce the desired performance. The integrated OWF with a synchronous generators (SG) system is studied under the conditions of changes in wind speed, a three-phase short circuit fault and the transient responses. An NIDC is proposed in this work to achieve simultaneous power flow control and stability improvement.

ANALYSIS OF SYSTEM MODELS
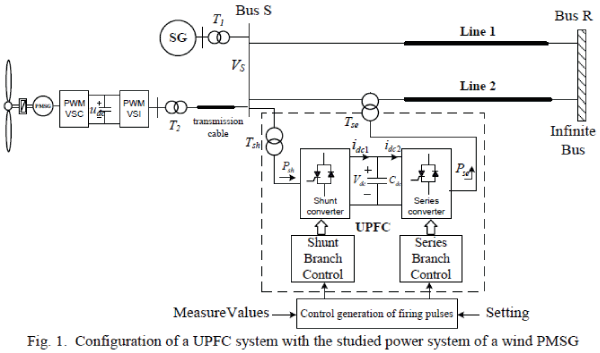
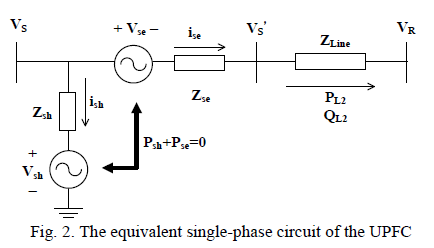
Fig. 1 shows the configuration of the system studied in this paper. The OWF represented by a large equivalent aggregated PMSG is driven by an equivalent aggregated wind turbine through the gearbox in [2]. The SG with a capacity of 555MVA is connected to a single-machine infinite-bus (SMIB) through a transformer T1 and two parallel transmission lines: Line 1 and Line 2. Line 2 contains the proposed UPFC located near Bus S. The aggregated OWF containing 200MW PMSG-based wind turbine generators is connected to Bus S through a T2 transformer and a 15 km transmission cable. The equivalent wind PMSG is driven by an equivalent wind turbine through an equivalent gearbox. The employed capacity of the proposed UPFC is 160 MVA, and its series voltage is added to Bus S voltage VS by the series connected transformer Tse. The shunt converter of the UPFC connected in shunt with the AC power system via a shunt transformer Tsh is primarily used to provide the real power demand of the series converter at the common DC link.
A. Wind Turbine Characteristics
The wind turbine input is the variable wind and the output is the mechanical power turning the generator rotor blades [4], [15].The output mechanical power available from a wind turbine can be obtained by
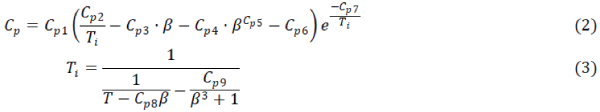image
image
image
where Cp1 to Cp9 are the wind turbine constant coefficients of Cp
B. PMSG
The wind generator chosen for this study is a three-phase PMSG, where the mechanical torque (Tm), electrical torque (Te) and dynamic equation can be found in [4]. The machine model of a PMSG can be described in the rotor rotating reference frame as follows [4]
image
and
image
image
The configuration of a field-oriented PMSG system consists of PMSG, a current-controlled PWM voltage source converter (VSC) and; vnverter (VSI), a field-orientation mechanism, including the coordinate translator, and a speed control loop. The input and output d, q axis voltages of VSC and VSI of wind PMSG could be expressed as
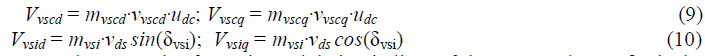image
image
image
C. Modeling of the UPFC
image
Under the synchronous reference frame, the d-q axis components of the series and shunt controllers are used to generate the direct and quadrature components of the modulated voltages. The direct and quadrature components of the voltages are then used to generate the modulation index and phase shift for the PWM module. The d-q axis voltages of series and shunt converters can be expressed as
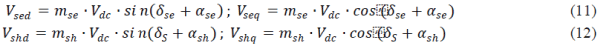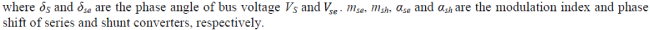image
image
The real and reactive power of series and shunt converter (Pse, Qse, Psh and Qsh), can be expressed as
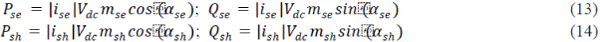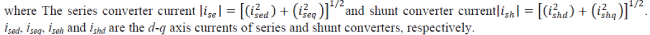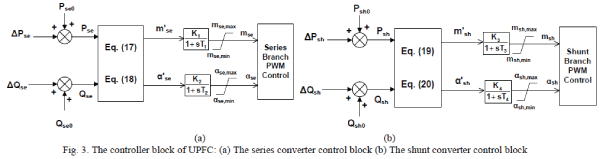
image
image
The controller block for the series and shunt converters of UPFC are shown in Figs. 3(a) and (b). Pse0, Qse0, Psh0 and Qsh0 are the initial values of real and reactive power for series and shunt converters. The mse, αse, msh, and αsh are provided to the PWM generator, which generates the gating signals for the power electronic switches in the series and shunt converters. They obtained by m’se, α’se, m’sh, and α’sh by its 1st order lag process, respectively, which can be expressed as
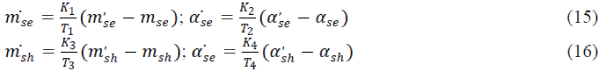image
and
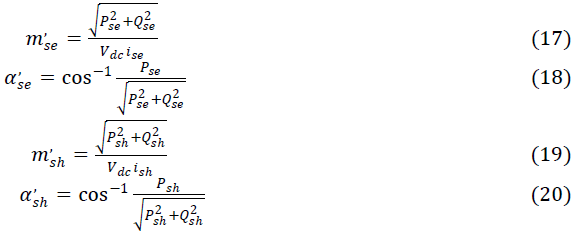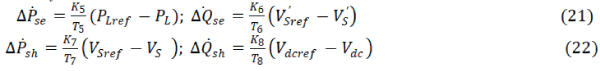image
image
image
image
image

THE PROPOSED NIDC FOR UPFC
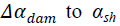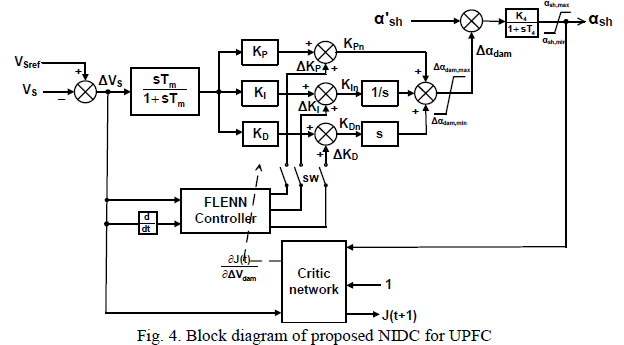The proposed NIDC consists of three parts: the adaptive critic network, the FLENN and PID linear damping controller, as shown in Fig. 4. The designed NIDC provides the training signal image to αsh of the UPFC shunt converter to improve the OWF system stability. An FLNN is adopted to implement the function expansion for the FLbased ENN to improve the accuracy of the function approximation. The adaptive critic network [16], [17] is applied in order to provide suitable training signals for the FLENN controller. The FLENN produce the variation gains values (ΔKP, ΔKI and ΔKD) of PID controller. The proposed NIDC is capable of providing near optimal results for complex and uncertain nonlinear system in order to solve the Hamilton–Jacobi–Bellman equation of optimal control [16], [17].
image
A. PID linear damping controller
The PID damping controller is analysis of complex eigenvalues based on a theory of modal control. The matrix of state space and the transfer function are follows as [18].
image
image
The winds peed is set 14 m/s for designing PID damping controller the UPFC, the transfer function T(s) [18] is represented as
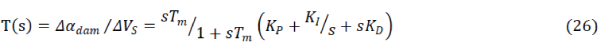image
where Tm is the time constant of the washout filter. KP, KI and KD are the gains for PID controller.
image
image
B. FLENN
Fig. 5 shows the design of the FLENN. It has an input layer, a hidden layer with a sigmoid function S(x)=1/(1 + e−x ), a context layer, and an output layer that is connected with an FLNN. The context layer is fed back to itself with a time delay z-1. The FLNN uses a feedforward neural network structure to generate a set of linearly independent functions, and functionally expands the elements of the input variables. The trigonometric function is used in the FLNN, since it can be computed more quickly than the Gaussian, sine and cosine functions. The input vector X=[X1, X2]T, which is a functional expansion that uses a trigonometric polynomial basis function, can be written in the enhanced space as ψ=[ψ1, ψ2,…ψp]=[1, X1, sin(πX1), cos(πX1), x2, sin(πX2), cos(πX2), X1X2], where X1X2 is the outer product term. Furthermore, the FLNN output is expressed by a linear sum of the yth node, as follows:
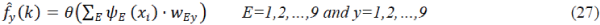image
image
The FLENN input 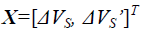image is used by the power system to directly transmit the numerical inputs to the next layer in this study. The context neurons of FLENN serve as memory units, as they store the hidden layer output signal. Therefore, the FLENN can employ the context neurons to increase dynamic characteristics of the network. The node output of the each layer of the FLENN and the superscripts present the layer-number of the output O, while the subscripts present the signal number of the related output, and these are given as follows.
image
where the wij is the connecting weights of the input layer to the hidden layer, while wrj is the connecting weights of the context layer to the hidden layer. α is the self-connecting feedback gain (0~1) of context neurons, and wjy is the connecting weight between the hidden layer and multiplication layer. The link weight wo at output layer is unity. The objective of the FLENN controller is to train the parameters wij, wrj, wjy and wEy to make the best match with regard to the control signal O(5) to generate ΔKP, ΔKI and ΔKD.
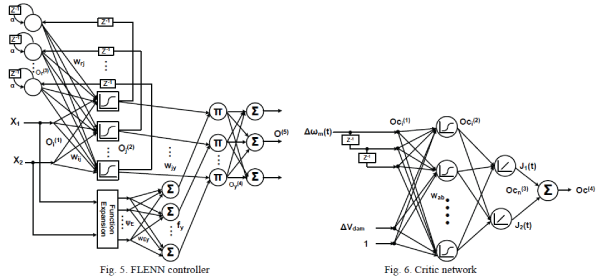image
C. Critic network
A critic network can be continuously trained forward in order to learn the cost-to-go function associated with the power system. This ability is of great importance for real time optimal control operations when there are changes in configuration and operating conditions. The cost-to-go function J of Bellman’s equation of dynamic programming estimated by the critic network is as follows [14].
image
where the utility function U(t) is an important effect to form the optimal cost-to-go function. γrepresents the discount factor (0~1). The utility function of the critic network is U(t), as follows.
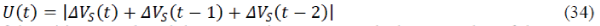image
The node output of the each layer of the critic network and the superscripts represent the layer-number of the output Oc, while the subscripts present the signal number of the related output, and these are given as follows.
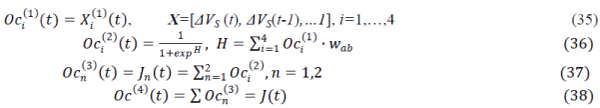image
where wab is the connecting weights of the input layer to hidden layer.
Using Eq. (34), the UPFC should improve the performance of bus voltage deviation ΔVS. The critic network in Fig. 6 has a four-layer feed-forward network structure. The training process ensures that the critic network provides optimal control to minimize the J(t), which enables the FLENN controller to provide the optimal parameters of PID controller to the UPFC in this paper.
D. The training process of FLENN and critic network
The gradient of the error function is the direction to which the function increases. Therefore, searching the opposite side of the gradient can force the cost-to-go function to be minimized. The gradient descent algorithm with the mean squared error function as the error function E can be defined by [16]
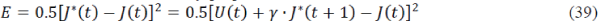image
where the J*(t) is the reference value of the cost-to-go function, which in the case of dealing with deviation signals is zero.
The changes in direct proportion to the amount that weights wab are modified, and can be used to produce the instantaneous estimates of the negative gradient. In order to use an on-line algorithm for the critic network and proposed FLENN, the gradient based on the chain rule can be represented as (40) and (41). The formulae for adjusting the wab of the critic network and weights WFLENN of FLENN are shown in by (42) and (43).
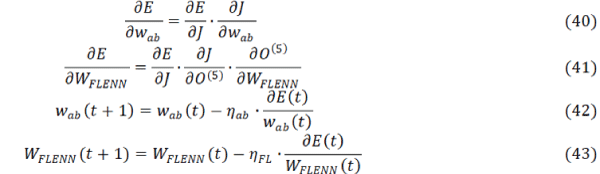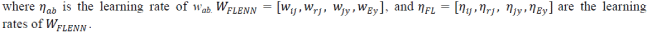image
image

CASE STUDIES AND SIMULATIONS
The proposed NIDC were simulated in this section. The damping controllers of SMIB plus the OWF system are compared with and without UPFC, with UPFC plus PID controllers while SW off, and with UPFC joined with the proposed NIDC while SW on in Fig. 4. The power system in Fig. 1 is simulated using PSCAD software, while the FLENN and critic network with GACO are achieved in a MATLAB 7.0 program. Three cases are described here to illustrate the proposed method.
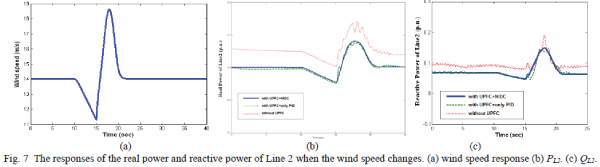
Case A: The stability of changes in wind speed
The wind speed is assumed to change from 14 m/s to 11 m/sat the 10th second, from 10 m/s to 19 m/s at the 15th second and from 19 m/s to 14 m/s at the 17th second in Fig. 7(a). Figs. 7(b) and (c) show the responses of the real and reactive powers of Line 2, respectively. It is found that the real and reactive powers of the OWF change with the variations of wind speed. When the UPFC is in service, the amplitudes of the real and reactive power changes can be reduced, and thus better control is achieved. The smallest amplitude changes on the real and reactive powers of Line 2 can be obtained when the proposed NIDC is installed with the UPFC. 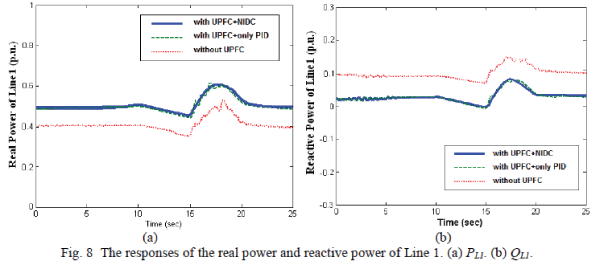Similar amplitude results can be found from the real and reactive powers of Line 1 shown in Figs. 8(a) and (b). Figs. 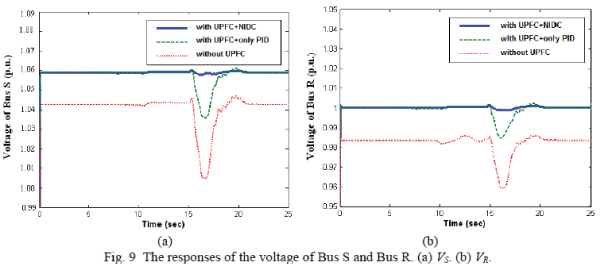9(a) and (b) show the responses of the voltage magnitudes of Bus S and Bus R, respectively. When the wind speed changes, the voltage magnitudes of Bus S and Bus R can also be found at the desired level. The voltage magnitudes of the two buses have the smallest variations when the proposed NIDC is joined with the UPFC.
Case B: Transient stability of the three phase fault
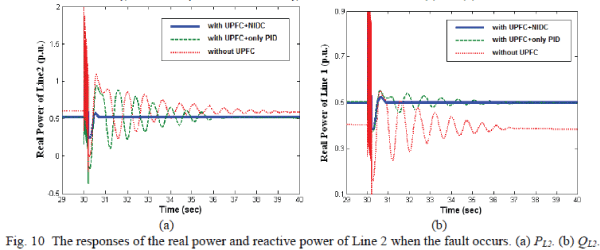
A three-phase short circuit with a duration of 0.1secondis simulated at the 30th second. The fault is used to compare the damping characteristics of the proposed scheme. When a fault occurs, Figs. 10(a) and (b) show that the UPFC with a PID controller (green line) can have better damping performance with regard to the real and reactive power on Line2 than the system without UPFC (red line). 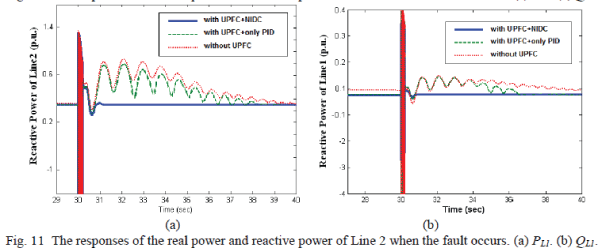It can be also seen that the proposed NIDC for UPFC (blue line) has the best damping effect on the transient stability for both real and reactive powers. 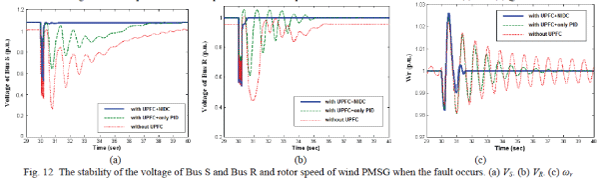Similar stability improvements can be also found from the transient stability of the real and reactive powers of Line 1 shown in Figs. 11(a) and (b). Figs. 12(a) and (b) also show that the UPFC with the NIDC can effectively improve the voltage transient stability of Bus S and Bus R. Fig. 12 (c) shows that the rotor speed of the wind PMSG (ωr) can quickly recover to the corresponding steady state when the system has the UPFC installed with NIDC, with better results than are seen with the systems that have UPFC plus only PID controller and without UPFC.
image
image
image
image
image
image

CONCLUSION
The results reported in this paper demonstrate the effectiveness of the proposed designed PID controller and NIDC for a UPFC with regard to improving the power control and stability of a grid containing a large-scale OWF and SG. The transient responses of the studied system subject to a three-phase short circuit fault show the effectiveness of the proposed method. Moreover, the online learning algorithms of the connective weights deviations of proposed FLENN and critic network were derived in this work. The control performance of the proposed NIDC shows that the method presented in this work can effectively stabilize the network under unstable conditions.

APPENDIX
image

References