ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| S.Sowmiya1, B.Raj narain2. Dept. of Electronics & Instrumentation Engineering Velammal Engineering College Chennai-66, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Adaptive filters play a vital role in digital signal processing applications. In this paper, a new approach for the design and implementation of adaptive filters say FIR and IIR are analyzed. The filter design is based on least pth norm algorithm and the characteristics of the individual filters are also taken into consideration. Least pth norm algorithm is considered for the design because it does not need to update weighting function and no constraints are involved during the course of optimization. Mostly the filter design is concentrated around the linear phase characteristics of the filters. With the help of minimax design of adaptive filters this approach helps to enhance the properties of LTI systems with good stability. The performances of the filters are analyzed in terms of exact noise cancellation using simulink model. With the help of MATLAB toolbox the filter properties are analyzed with various plots and tables. The simulation results of both FIR and IIR filters enables us to achieve good signal to noise ratio with the analysis of stability, causality and convergence of the filters are verified with varying coefficients.
Keywords |
| adaptive filters, FIR, IIR, least pth norm algorithm, LTI, minimax, MATLAB. |
INTRODUCTION |
| In signal processing and control applications, the signals and the transfer functions of the system are time invariant and should be known at the design time. Designing filters and controllers to achieve the desired results is necessary. In many applications, the signals to the system, transfer functions of the system and the system environment is time varying. In some applications like active noise and vibration control, the system to be controlled is unknown during the design. In such cases, a self adjusting filter is required to adapt to the changing environment to meet the desired specifications. This leads to the occurrence of adaptive filters which provides good consistency and better performance. To construct an adaptive filter the filter structure whether to use an IIR or FIR filter for the design is considered initially and then the algorithm which meets the desired results are then chosen for implementation. Algorithm plays a vital role in the design of adaptive filters. This paper deals with the design of both FIR and IIR adaptive filters. Among various different kinds of algorithm available for the design of adaptive filters least pth norm algorithm is described. Further a low pass FIR and IIR adaptive filter is proposed using least pth norm algorithm and the filter properties such as stability, causality and convergence rate of both the filters are analyzed using various plots and graphs for increasing coefficients. |
ADAPTIVE FILTERING |
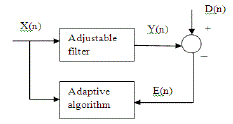
| An adaptive filter is a device that models the relationship between two signals in real time in an iterative manner. Adaptive filters are realized as a set of instructions running on an arithmetic devices such as digital signal processor (DSP) chip or in a custom VLSI integrated circuit or as a set of logic operations implemented in a field programmable gate array. Adaptive filtering involves the process of varying the parameters so as to adapt to the changes in the signal characteristics. An adaptive filter is a filter that itself adjusts its parameters in order to minimize the error at the output. Over the past three decades, digital signal processors have made great advances in increasing speed, reducing complexity and power consumption. As a result, adaptive filtering algorithms had become more practical and essential for the future of communications, both wired and wireless. The adaptive filter design requires the filter structure and the basic adaptive filtering algorithm for simulation. In order to define the self-learning process, care should be taken in selecting the algorithm which provides minimal difference between the actual output and the desired output is chosen. There are different kinds of algorithms that are used for the design of adaptive filters. The adaptive filters are selected depending on which method is to be used to update the coefficients of the adaptive filters and whether to use an IIR or FIR filter. Care should be taken in selecting the proper adaptive filtering algorithms which provides desired specification since adaptive filtering act as a heart for the adaptive filter design. The algorithms are then practically implemented so as to achieve quick convergence of the filter coefficients and to provide better performance. The basic structure of adaptive filter is shown in fig.1. |
 |
FIR And IIR Filter Structures |
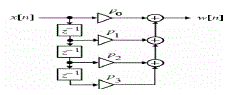
| An adaptive digital filter structure can be built up either using Finite Impulse Response (FIR) filter or by using Infinite Impulse Response (IIR) filter. Both FIR and IIR filter structures can be built in many different ways and with different basic structures. The most commonly used FIR filter structure is the transversal filter which implements all zero filter with a canonic direct form. FIR filter is inherently stable because it involves forward path only. FIR filter structure does not have the feedback path as in IIR. The presence of feedback to the filter structure lead the filter become unstable and leads to the occurrence of unwanted oscillations. Because of this the IIR filter remains unstable due to the presence of feedback. For this adaptive filter the output is a linear combination of adaptive filter coefficients. This stable structure of FIR filter improves the system performance in terms of convergence speed. For simple implementation and to reduce the computation complexity most IIR filter structure uses the canonic direct form realization. Some other realizations are also considered to overcome the drawbacks of cascade realization like slow convergence and the need for stable monitoring. The direct form realization of FIR filter structure is shown in fig. 2. A causal FIR filter structure of order N is characterized by the transfer function of the filter H(z) represented as |
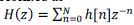 |
 |
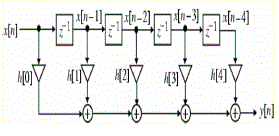
| The direct form realization of IIR filter structure is represented as shown in figure 3. A casual IIR filter of order N is characterized by the transfer function of the filter say H(z) represented as |
 |
| FIR and IIR systems are distinguished by the impulse response which does not exactly become zero but continues definitely. In contrast, the impulse response of FIR filter becomes zero at times t>T, whereas the impulse response of IIR filter usually approaches zero but can be neglected at certain point. FIR filters are preferred the most than IIR filters because they have linear phase response and are non-recursive in nature. IIR filters are not preferred most because they are recursive and feedback is also involved. FIR cannot simulate analog filter response whereas IIR filter can simulate the response accurately. These kinds of filter structures are involved in the design of adaptive filters so as to achieve desired specifications. The performance of the filter is adjusted by varying the coefficients of the filter in order to minimize the difference between the actual output and the desired output. |
LEAST PTH NORM ALGORITHM |
| While designing adaptive filters it is good to have enough knowledge about the algorithm for efficient filter design. It is important to have a system based approach so that the design can be done systematically and efficiently with minimum cost. |
| Among different kinds of algorithms that have been involved to update the coefficients of adaptive filters least pth norm algorithm is used more because of its reduced computational complexity and robustness. But the need for filter is to minimize the error between actual output and desired signal which is achieved efficiently by means of Least Pth Norm algorithm. This method does not need to update weighting function because it is an unconstrained convex minimization approach. This approach improves the filterquality and provides results regarding high causality and stability with the help of pole zero plots. This algorithm also provides larger gradient that makes it to converge faster when away from optimum. Then Pth norm filter coefficients are applied to achieve the analysis parts. For reconstruction, using inverse filtering and interpolation the input signal is reconstructed to calculate reconstruction error to verify the system functionality. The proposed design procedure can be used to design a wide variety of analysis/ synthesis filter banks with different structural and performance constraints. This impacts the quality of the resulting overall analysis /synthesis system. To check the perfect reconstruction quality of the designed filter bank the signal- to- reconstruction noise ratio was used as a measure of reconstruction performance where the inputs and output signals are and k is the system delay. This algorithm provides exact noise cancellation for higher order filter structures with increased norm valueswhereas LMS algorithm does not fit for increasing order of the filters. Hence designing filters of higher order are made easier with least pth norm algorithm with increase in the normalized values. |
SIMULATION RESULTS |
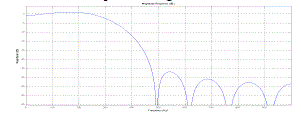
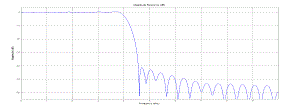
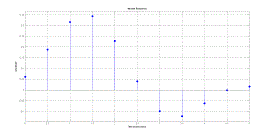
| The simulation results of both FIR and IIR filters are analyzed from the adaptive filter design implemented in MATLAB using least pth norm technique. Depending upon the order of the filter the characteristics of the filter and its coefficients are also varied. Results obtained for ten coefficients and fortycoefficients of both FIR and IIR filters are presented.The filter properties such as power transition, causality, stability and region of convergence are determined from their corresponding magnitude response, impulse response, step response and pole zero plots. With the help of the simulation results obtained from the filter mathematical model, the performance of the filters is analyzed. The filter with higher coefficients and those with minimal coefficients are compared with their responses to predict the performance of the filter with least pth norm algorithm. |
 |
 |
 |
CONCLUSION |
| The aim of the paper was to compare the performance parameters of both finite impulse response and infinite impulse response filters that were simulated in MATLAB using least pth norm algorithm. As the coefficient order increases the use of multipliers and additions per unit sample also tend to increase for both the filters. With increase in filter order the computation complexity of FIR filter increases, whereas computation complexity is reduced in IIR filter structure by the help of feedback. The presence of feedback in IIR filter makes the system to behave less stable than FIR filters. The use of Least Pth Norm algorithm eliminates unwanted noise at all frequency range of an input signal irrespective of number of coefficients. It also been inferred from the results that FIR filter designed by means of normalized algorithm provides fast convergence of signal with high throughput and stability. Also FIR provides excellent estimation of input signal than IIR filter. The magnitude response, impulse response and the corresponding pole zero plot of both the filters are analyzed to determine the convergence rate, causality and stability of the filters. The use of least pthnorm algorithm provides better gain also it reduces the ripple content in the output and smoothens the response at the stop band. The future scope of this paper is to synthesize the simulated model of both FIR and IIR filters in VHDL language and the parameters of the filters say power dissipation, speed and efficiency are analyzed and the desired filters is then implemented into a SPARTAN3 FPGA board using XILINX synthesizer tool. |
References |
|