ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Divyashree N P 1, Sowmya K S 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Pseudo-random number generators (PRNGs) are a key component of stream ciphers used for encryption purposes. While Non linear Feedback Shift Registers (NFSRs) combined with cellular automata has been utilized for PRNGs, the use of cellular automata (CA) is another viable option. This paper explores the combination of NFSRs and CA as the key components of an efficient stream cipher design for implementation on Field Programmable Gate Arrays (FPGAs). The proposed stream cipher design builds upon a recent published design known as A2U2, which uses the principles of stream cipher and approaches from block cipher design. Comparisons with the A2U2 design indicate that the use of CA have the potential to improve the quality of the random numbers generated and hence increase the security of the cipher.
Keywords |
| Cellular Automata, Linear/Non-linear feedback shift register, Stream cipher, Pseudo random number generator. |
INTRODUCTION |
| Stream-ciphers represent an important class of encryption hardware that target applications with tight constraints on logic gates and memory or where high-throughput is necessary. For example, RFID tags are being used in a wide range of applications, many requiring secure transmission of identifying information and other data. Due to the tight limits on power and hardware resources, steam ciphers are attracting interest over the more complex block cipher designs for implementation in RFID tags[1]. The stream ciphers process data one bit at a time. The bit size of the stream cipher is typically one bit or byte. The key size is longer or equal to the memory size. The stream ciphers are symmetric. A key challenge in the design of a good stream cipher is to balance an efficient hardware implementation while making it difficult for an adversary to decrypt the transmitted data. The main component of the stream cipher is the key stream generator, which can be viewed as a pseudo-random number generator (PRNG). |
| Important metrics for the performance of the PRNG’s are speed, area and power dissipation, while producing high quality random numbers. A linear feedback shift register (LFSR), which is implemented from cascade of flip flops and a few XOR gates typically forms the core of the PRNG. In addition, non linear feedback shift registers (NFSG’s) must be included in a key stream generator design to remove the linearity in the encrypted cipher text, making it more difficult for an adversary to discover the secret key. The impact of adding cellular automata (CA) to the key stream generator is considered. The implementation of CA is relatively straightforward using FPGA’s due to their nearest interconnectivity and regularity in their physical layout which has allowed FPGA technology to implement more complex designs that were formerly the exclusive domain of ASIC designs. This project is focused on the implementation of an efficient stream cipher using FPGA technology as a proof of concept, this technology is easily transferable to VLSI technology. The stream is based on A2U2 stream cipher. The A2U2 stream cipher is a hardware based stream cipher proposed for extremely resource limited devices such as RFID tags. The importance of such ciphers are further highlighted by novel manufacturing technologies, such as printed ink to develop extremely low cost RFID tags. |
| The main objective of this paper is to generate a good quality random number using the concept of cellular automata for the resource limited devices and provide the security to this hardware devices. It also serves to improve the resistance of cipher from various forms of cryptanalysis such as correlation attack and algebraic attacks[6]. The use of non-linear feedback shift register (NFSR) and cellular automata (CA) as a pseudo random number generator (PRNG) makes the cipher to be encrypted randomly and makes the adversary difficult to decrypt the information or data. |
| This paper is organised as follows: Section II describes the background and the previous work carried out. Section III includes the proposed design. Section III has the block diagram which is used in the design of the stream cipher using cellular automata. Section IV includes the research method carried out for the proposed design and the simulation results and Section V has the conclusion and future work. |
BACKGROUND AND PREVIOUS WORK |
| The A2U2 stream cipher is composed of four distinct building blocks. The four elements include: i) a counter, ii) a combination of two nonlinear registers, iii) an irregular change in the feedback function through a key-bit mixing mechanism, and iv) a filter function. An overview of the cipher design is illustrated in Fig. 1. |
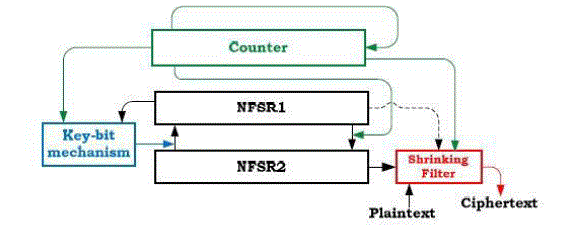 |
| A. The Counter |
| The counter is a 7-bit Linear Feedback Shift Register (LFSR). Its feedback function is a maximal length polynomial function FC (whose period is 27-1). |
| B. The Two Nonlinear Registers |
| This part of the cipher (as well as the counter) has been freely inspired by the block cipher KATAN , which introduces a new combination of two NFSRs, where the feedback function of each NFSR provides the feedback to the other NFSR. |
| C. The Irregular Key-bit Mechanism |
| The third component of A2U2 is a function of key-bit mechanism. It increases the complexity of the cipher and modifies its feedback function, using the securely stored 56-bit private key. |
| D. The Filter Function |
| The final building block of A2U2 is the filter function, named the “shrinking filter” in reference to the clock controlled generator design of the Shrinking Generator. |
PROPOSED METHOD |
| This section describes the basic concept of stream cipher design and overviews the key components, the linear feedback shift registers (LFSRs) and cellular automata (CA). A review of previous works in stream cipher design is also given. The proposed stream is based upon the A2U2 stream cipher. The A2U2 stream cipher is a hardware-based stream cipher proposed for extremely resource limited devices such as RFID tags [1]. The KATAN [2] and A2U2 [1] cipher utilize a pair of nonlinear feedback shift registers (NFSRs) in the main part of their design. The use of an NFSR instead of an LFSR improves the resistance of the cipher from various forms of cryptanalysis, such as correlation attacks and algebraic attacks [6]. As noted by Hortensius et al. the quality of the random number sequence generated by a cellular automata-based register is better than that of an LFSR [3]. The proposed stream cipher combines the A2U2’s design principle with the cellular automata implementation. |
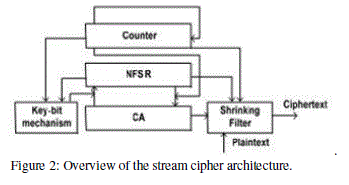
| It consists of a 17 bit non-linear feedback shift register NFSR as the A2U2 stream cipher but replaces the shorter-length NFSR of the A2U2 with a 9 bit maximal length cellular automata as depicted in Figure 2. |
| The proposed stream cipher is composed of five different blocks. The five blocks are: i) a counter, ii)a 17 bit long nonlinear feedback shift register iii) a 9 bit long cellular automata iv) a key bit mixing mechanism and v) a filter function, which does the function of a simple multiplexer. The overview of the proposed stream cipher is shown in Figure 2 |
 |
| The proposed stream cipher uses the LFSR-based counter (see Figure 3) as in the A2U2 stream cipher because it has already been optimized to reduce the number of gates. |
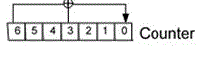 |
| The feedback function of the counter is defined as: |
| where‘ ^ ’ indicates the XOR operation and C [i] represents the ith counter bit. Regarding the interconnection between the NFSR and CA, the feedback of the NFSR provides the feedback to the CA and vice versa, as shown in Figure 4. The feedback functions for the CA and the NFSR are represented by the following polynomial: |
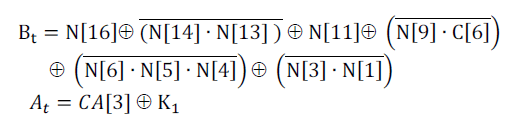 |
| where C[i], N[i] , CA[i] and Ki represent the ith counter bit, ith NFSR bit, ith CA bit, and the key bit generated by the keybit mechanism, respectively. |
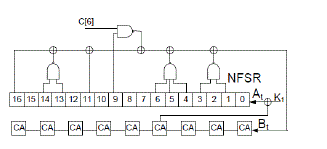 |
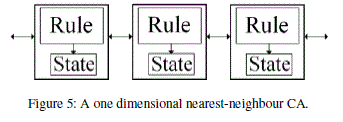
| An important part of the proposed stream cipher design is the CA implementation. A cellular automata with binary state values can be viewed as an array of cells where each cell can assume either the value 0 or 1. The CA will evolve in discrete time steps, where the next state of each cell interacts with their immediate neighbours based upon a local rule. A general configuration of a one dimensional CA with binary state values and a neighbourhood consisting of the cell’s own state and those of its immediate neighbours is shown in Figure 4. In a one dimensional CA, there can be a total of eight distinct neighbourhood configurations with a total number of 256 distinct mappings from all the neighbourhoods to the next state. Each mapping is defined as a rule of the CA. A pictorial representation of Rule 90 [7] is illustrated in Figure 5, where the top row represents the eight possible states for a three-cell neighbourhood and the bottom row represents the next state for the cell of interest. |
 |
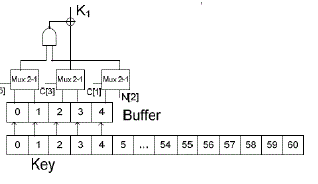
| The other component of the proposed stream cipher is the key-bit mixing mechanism. The key-bit mechanism as shown in Figure 7, increases the complexity of the stream cipher making it harder to crypto-analyse. |
| The output bit K1 is XORed with the CA bit 4 and provides the feedback to the NFSR. The key is generated using the same process as the A2U2 stream cipher. As illustrated in the Figure 7, at every round, five bits of the key are loaded into a buffer. Finally, these bits are combined with three bits of the counter and one bit of the NFSR as shown below: |
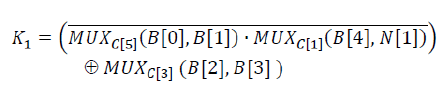 |
| The block diagram of the key-bit mechanism is shown in the below |
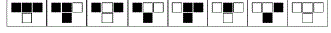 |
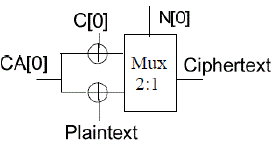
| The last component of the proposed stream cipher is the filter function. The filter function ensures that only the part of the input string coming out from the CA-based register will be XORed with the plaintext based on a selector string provided by the NFSR.The filter function shown in Figure 8 is represented by the following equation, |
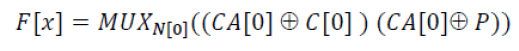 |
| where P represents the plaintext. |
 |
RESEARCH METHOD AND SIMULATION RESULTS |
| In the design of stream cipher using the concept of cellular automata as a proof of concern we have taken the voice as the input data. The input voice is taken and through Matlab where the voice is converted into text format for which the separate matlab programs are written and thus the original text is obtained which is taken into the data base of the Xilinx program. Separate programs are written for the each blocks in the design of the stream cipher using verilog language of Xilinx12.2 and the programs are simulated using the modelsim 6.3f simultor.The design flow for the paper is carried out as follows: |
 |
| The program written is synthesized using the synthesizer in the Xilinx and the resistor transistor logic (RTL) schematic for each block is obtained. The device utilization summary is noted down in each case. |
| The stream cipher counter is used to minimize the gates utilized in the design and can be easily implemented on the Spartan 3 FPGA. As known from the previous work, that is by using the principle of A2U2 the counter has been optimized to obtain the minimum number of gates and area occupied by it is less and has the better performance and power which is being checked using the simulation results obtained from each block in the proposed design. The results are obtained on the equations given in the above section and with the block operation. |
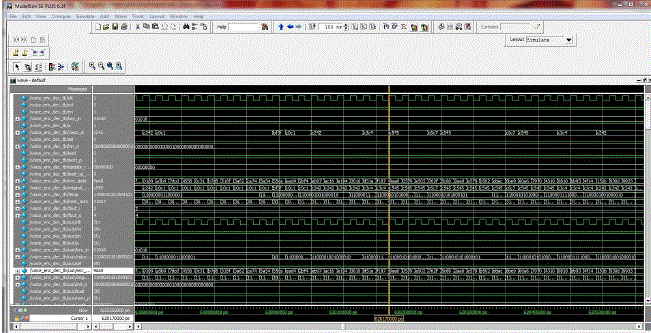 |
| The simulation result contains the input voice(original data), the encrypted data which is encrypted on the basis of the design which we have implemented using the concept of cellular automata and the decrypted data (original data). |
CONCLUSION AND FUTURE WORK |
| The impact of adding cellular automata in the core of the PRNG (pseudo random number generator) shows that the data is encrypted with a better quality random number and is suitable to implement it on the Spartan 3 FPGA. The use of A2U2 based counter minimizes the number of gates used. Thus with the use of the concept of cellular automata (CA) the data can be secured by various forms of cryptanalysis. Future work includes the use of heterogeneous CA and for the use for various other applications. |
References |
|