ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
P. S. Noori Banu1, S. Devaki Rani2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In the current study, an artificial neural network (ANN) model was developed to predict the properties of alpha and near alpha titanium alloys as a function of their composition. The input parameters of the ANN model consist of composition and heat treatment parameters of alpha and near alpha titanium alloys. Property parameters such as tensile strength, yield strength, percentage elongation, reduction in area, Charpy impact, rock well hardness, modulus of elasticity-tensional, modulus of elasticity-torsional, electrical resistivity and thermal expansion were included as the output parameters. The experimental datasets of thirteen (seven alpha and six near alpha) alloys were used for training. The predictability of each property using this model has been evaluated in terms of accuracy, correlation coefficient (R) and average absolute relative error (ARRE). Our study was able to predict the properties of titanium alloys with good accuracy. The results obtained were compared to the experimental data and are found to be consistent. The developed model can be used as a working as well as guiding tool for the design and development of alpha and near alpha alloys. Further, temperature-dependent effects on properties were evaluated using linear regression models.
Keywords |
| Artificial Neural network; alpha (α) and near α titanium alloys; composition; properties. |
INTRODUCTION |
| Titanium alloys have low density and excellent strength-to-weight ratio allowing lighter and stronger structures with superior corrosion and erosion resistance in different environmental conditions [1]. High temperature range (300-6000C) capability, high toughness of these alloys resulted in their usage in making of air craft structural components, gears, components of turbine engine and bio-medical devices [2]. In general, the titanium alloys are classified as α, near-α, α+β, near – β, metastable β and stable β depending on their composition in terms of the ratio of the α and β phases in binary β-isomorphous phase diagram. The sub classes near -α and near-β refer to alloy with compositions which place them near to α/(α+β) or (α+β)/β phase boundaries respectively [3]. |
| Alpha alloys have relatively large amount of alpha stabilizers i.e. Al, Sn, O and N; and low concentrations of beta stabilizers i.e. V, Mo, Fe and Cr. Alpha alloys that contain Al, Sn and/or Zr are preferred for high temperature and cryogenic applications. Near alpha alloys can be obtained from the alpha alloys by adding traces of beta stabilizing elements. These are somewhat heat treatable [4]. |
II. RELATED WORK |
| Depending on the application of alpha and near alpha titanium alloys, there is a need to modulate the microstructure and properties of these alloys. Several modeling techniques are currently being used to achieve this objective. The experimental techniques are microscopy, synchrotron radiation X-ray diffraction and differential scanning calorimetryetc. The physical modeling methods include thermodynamic modeling, the Johnson-Mehl- Avrami method, finite element modeling, the phase-field method, the cellular automata method, crystallographic and fracture behavior studies and atomistic simulations of interfaces and dislocations [3]. Neural network models are one of the most powerful modeling techniques based on statistical approaches with a very quick return for the practice. These models are suitable for simulations and correlations that are hard to be described by the physical models. Artificial neural network (ANN) is a non-linear statistical technique [5] that can explore non-linear relationships between the input and the output variables. It can be applied for alloys for predicting their properties at different temperatures and at different compositions whose relationships are non-linear in nature. |
| In the present work, we have attempted to develop a constitutive ANN model to predict the properties of alpha and near alpha alloys based on the composition. The properties of these alloys show complex non-linear relationships with their composition. Further, the temperature-dependent changes in tensile strength, yield strength and percentage of elongation were explored using linear regression analysis. Such model will help in designing alpha and near alpha alloys based on the properties required as well as based on the applications. |
III. METHOD |
| For neural network modeling, seven α-alloys i.e. Ti-0.3Mo-0.8Ni (grade12), Ti-3Al-2.5V (Grade 9), Ti-3Al-2.5V- 0.05Pd (Grade 18), Ti-3Al-2.5V-0.1Ru (Grade 28), Ti-5Al-2.5Sn (Grade6), TI-5Al-2.5Sn-ELI and Ti-6AL-2Nb-1Ta- 0.8Mo; and six near α-alloys i.e. Ti-8Al-1Mo-1V, Ti-6Al-2Sn-4Zr-2Mo-0.1Si, Ti-6AL-2Sn-4Zr-2Mo, Ti-2.25AL 11Sn-5Zr-1Mo-0.2Si, Ti-5AL-5Sn-2Zr-2Mo-0.25Si, Ti-6AL-2Sn-1.5Zr-1Mo-0.35Bi-0.1Si were used. |
| The experimental data regarding α- and near α-titanium alloys was collected from the existing literature. The composition data of alloys (C, N, O, Fe, Al, V, Pd, H, Mo, Ni, Ru, Sn, Zr and Si) were used as the input variables. The properties of alloys such as tensile strength, yield strength, percentage elongation, reduction in area, Charpy impact, Rockwell hardness, modulus of elasticity- tensional, modulus of elasticity- torsional, electrical resistivity and thermal expansion were used as the output variables. Forty one data sets for the thirteen titanium alloys at different temperatures were selected. From these data sets, thirteen data sets showing properties of the titanium alloys at ambient temperature were selected for constructing an ANN model and for its validation. |
| An ANN model was constructed to predict the various properties of these titanium alloys as a function of their composition. This model consisted of an input layer, an output layer and two hidden layers. Table 1 depict the mean, standard deviation and range of all the input and output variables of datasets used for training, validation and testing. Training was stopped when the root mean square error (RMSE) was reduced to 0.0001. The number of hidden layers and the number of neurons was fixed based on RMSE. |
Statistical analysis |
| Mean and standard deviation of the input and the output parameters were calculated using Graph pad prism software. Linear regression analysis was carried out to study the impact of temperature on tensile strength, yield strength and elongation using the computational website www.xuru.org. Three dimensional (3D) plots were constructed to explore influence of binary variables on the properties using CurveExpert Professional version 2.0.4. software. |
 |
 |
IV. RESULTS AND DISCUSSION |
| Artificial neural network (ANN) is an excellent learning tool for exploring the intricate non-linear relationships between 'n' number of inputs and 'n' number of outputs and process the information akin to biological neuron networking in its hidden layers. The success of ANN model primarily depends on the efficiency of training of feedforward neural networks using the back-propagation (BP) learning algorithm. To achieve greater efficiency to this model, we have incorporated all the experimental datasets available in the literature regarding the composition and properties of alpha and near alpha alloys. |
| From the data of all the thirteen alloys, nine data sets were included in the training dataset and the independent test dataset included the data of all thirteen alloys as shown in Table 1. As the ANN model had been well trained based on the training dataset, the selected test dataset was used to test the generalization property of the trained network under a fixed composition. To increase the convergence speed and accuracy within the network, uniformity in units of measurement was maintained in all the experimental data (both input and output parameters). |
| In the current model, two hidden layers are adopted to ensure high training accuracy. The number of neurons in each hidden layer was adjusted so as to minimize inefficiency in learning process and to maintain convergence rate. Supplementary file 1 depicts the number of neurons, complexity of intricate relationships between composition and properties, and ANN algorithms used to predict the properties of alpha and near alpha titanium alloys. |
 |
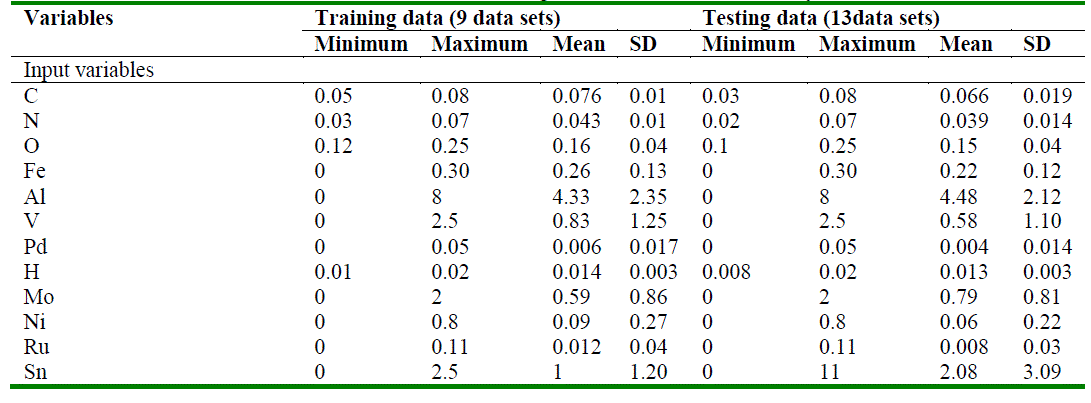
| X-axis: Alloys; Y-axis: Property of alloy; 1, 2, 3, 4…., 13 are thirteen α/near α-titanium alloys. a) Tensile strength (MPa); b) Yield strength (Mpa); c) % elongation in 51 mm gage length; d) Reduction in area (%); e) Charpy impact (J); f) Hardness (HRB). Blue and Red lines depict experimental and predicted data, respectively. |
| Predictability of ANN |
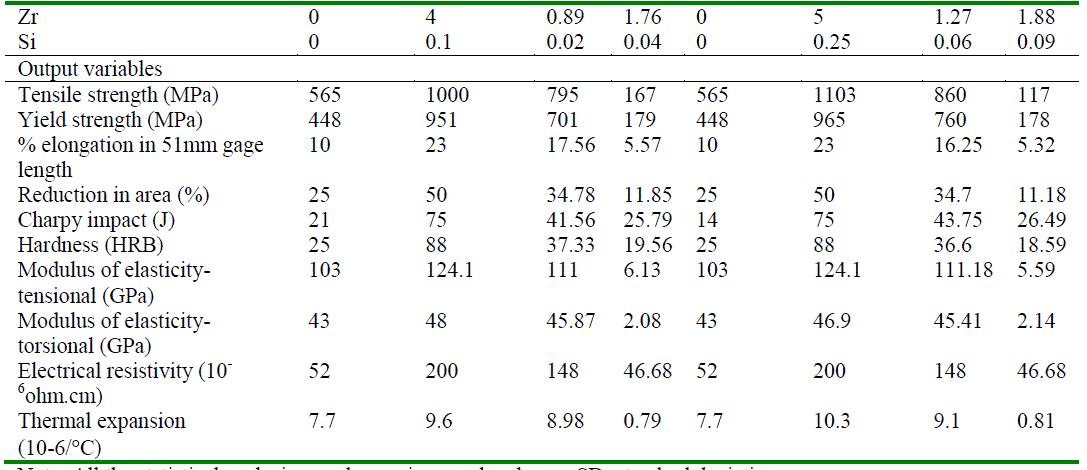
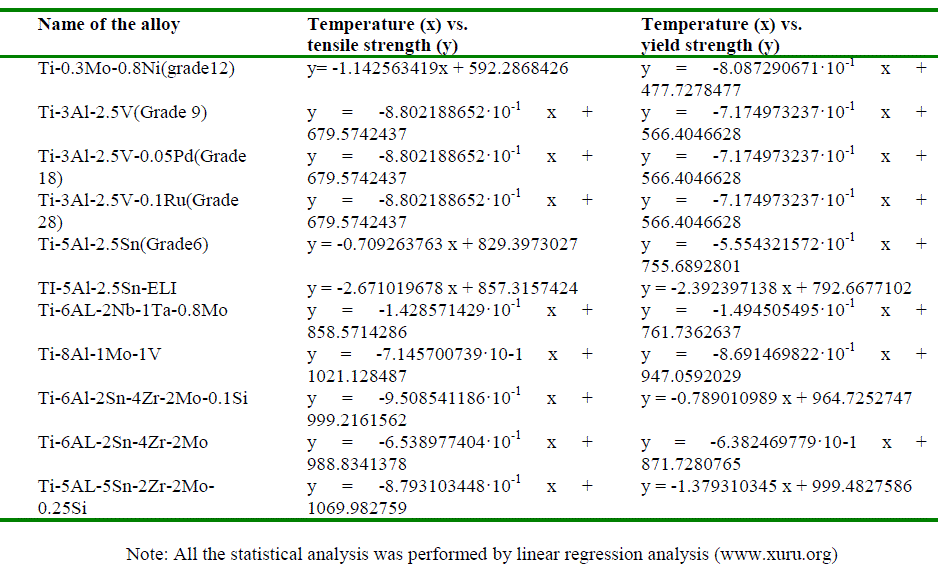
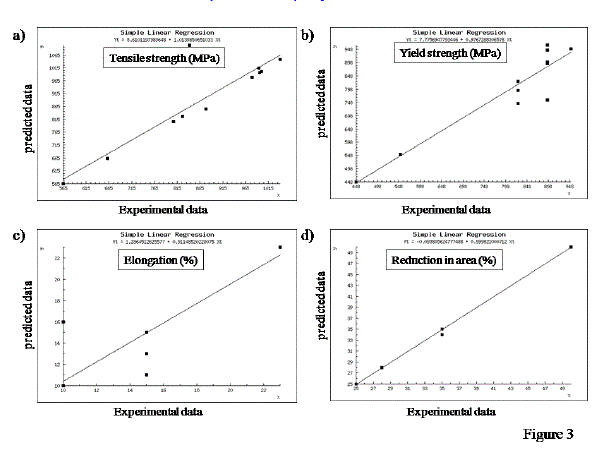
| The experimental data vs. predicted data of the thirteen alloys were plotted for each property (Fig 1 and Fig 2). As show in Table 2, the developed ANN model predicted reduction in area, modulus of elasticity-tensional, modulus of elasticity-torsional and electrical resistivity with 100% accuracy. The prediction accuracy for tensile strength, % elongation and thermal expansion was 92.3%. The prediction accuracy for yield strength and Charpy impact was 84.6%. Fig 3 and Fig 4 showed good correlation between the experimental data and the predicted data (correlation coefficient, R = 0.90 – 1.00). The narrow mean absolute error and good correlation between the experimental and predicted values further strengthen the accuracy of this model in predicting the properties of α and near α-alloys based on their composition. |
| Interestingly, this trained ANN predicted unknown value of the modules of elasticity-torsional for Ti-6Al-2Sn-4Zr- 2Mo-0.1Si as 44. However, this data need to be validated experimentally. |
 |
| X-axis: Alloys; Y-axis: Property of alloy; 1, 2, 3, 4…., 13 are thirteen α/near α-titanium alloys. a) Modulus of elasticity-tensional (GPa); b) Modulus of elasticity-torsional (GPa); c) Electrical resistivity (10-6ohm.cm); d) Thermal expansion (10-6/ïÃâðC). Blue and Red lines depict experimental and predicted data, respectively. |
 |
 |
 |
| X-axis: Experimental data; Y-axis: data predicted by ANN. a) Charpy impact (J); b) Hardness (HRB); c) Modulus of elasticity-tensional (GPa); d) Modulus of elasticity-torsional (GPa); e) Electrical resistivity (10-6ohm.cm); f) Thermal expansion (10-6/ïÃâðC). |
| Effect of elevated temperatures on the properties of alloys |
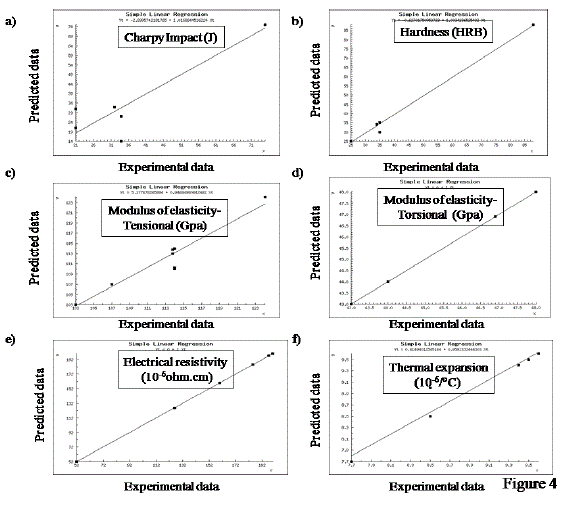
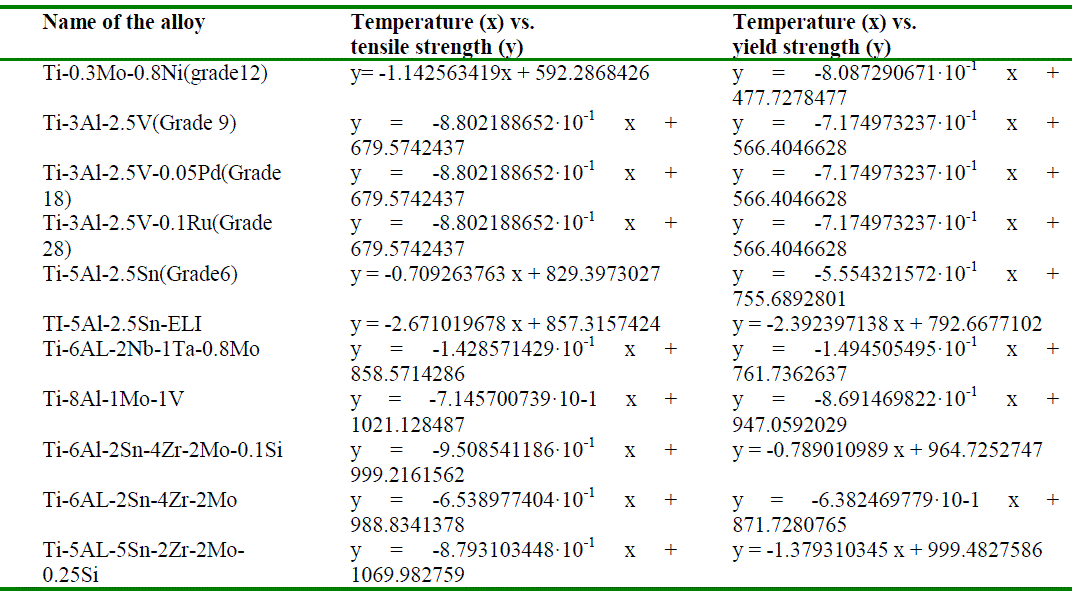
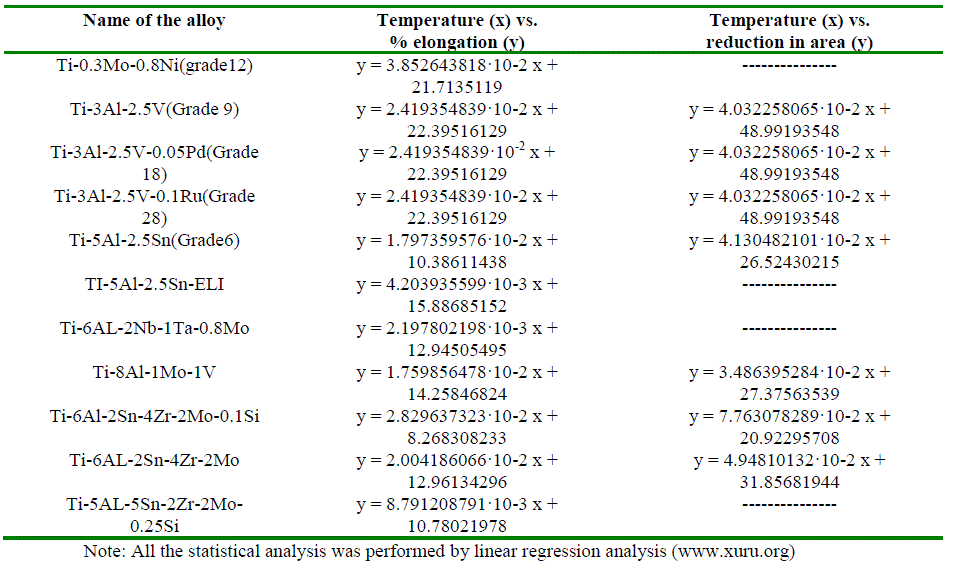
| Linear regression analysis was performed to study the impact of increase in temperature on the properties of alloys (Table 3 and Table 4). These models (Y = mX + C) serve as good indices in understanding alloy related (C) and temperature-dependent (m) effects on the properties. As shown in Table 3, there is decrease in tensile strength and yield strength with increase in temperature in all the alloys. Three alloys i.e.Ti-3Al-2.5V (Grade 9), Ti-3Al-2.5V- 0.05Pd (Grade 18) and Ti-3Al-2.5V-0.1Ru (Grade 28) have similar tensile strength as well as yield strength. They exhibited similar changes in these properties at elevated temperatures, which is probably attributed to similar 'Al' content. Ti-6AL-2Nb-1Ta-0.8Mo exhibited the lowest decrease in tensile strength and yield strength with increase in temperature. TI-5Al-2.5Sn-ELI exhibited the highest decrease in tensile strength and yield strength with increase in temperature. |
| As shown in Table 4, Ti-3Al-2.5V (Grade 9), Ti-3Al-2.5V-0.05Pd (Grade 18) and Ti-3Al-2.5V-0.1Ru (Grade 28) showed similar temperature-dependent effects in terms of percentage elongation and reduction in area. With increase in 'Al' content, there is decrease in elongation and reduction in area. Incorporation of 'Si' also showed similar trend. Ti-6AL-2Nb-1Ta-0.8Mo exhibited the least increase in % elongation with increase in temperature while Ti-0.3Mo-).8Ni (grade12) showed maximal increase in % elongation with increase in temperature. |
 |
 |
Effect of binary variables on the properties of alloys |
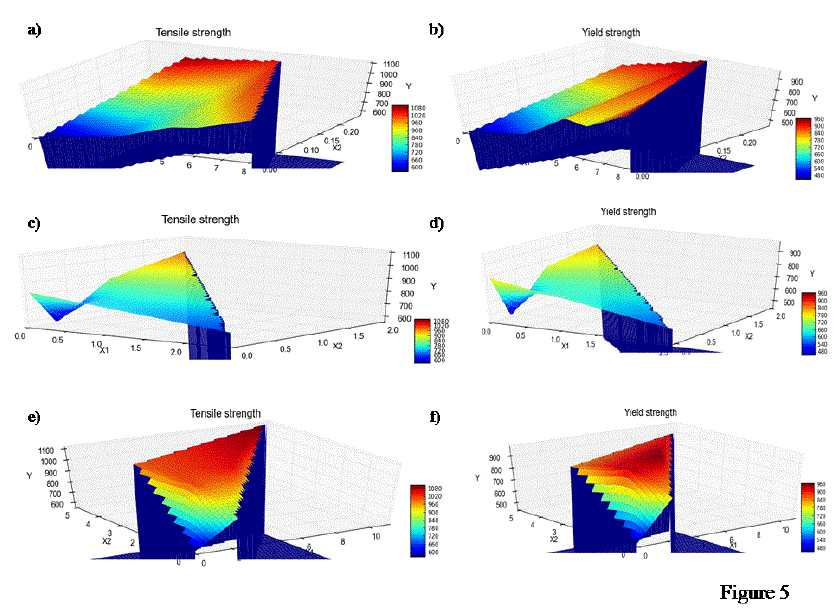
| Three dimensional (3D) structures were generated as shown in Figure 5 to illustrate the influence of bivariate models on tensile strength and yield strength. Figure 5a and Figure 5b suggests that with increase in 'Al' composition , there is increase in tensile strength as well as yield strength, which corroborated with results of earlier simulations [6]. These figures further suggest the synergistic effect of 'Si' in augmenting tensile strength and yield strength. This is further clarified by the observation showing higher yield strength of Ti-6Al-2Sn-4Zr-2Mo- 0.1Si in comparison with Ti-6AL-2Sn-4Zr-2Mo. As shown in Figure 5c and Figure 5d, there is no effect of 'V' composition on tensile strength and yield strength while 'Mo' composition increased both tensile strength and yield strength. As shown in Figure 5e and Figure 5f, the composition of 'Sn' and 'Zr' increases tensile strength and yield strength significantly. This is further supported by the raw data of three alloys i.e. Ti-2.25AL-11Sn-5Zr-1Mo-0.2Si, Ti-5AL-5Sn-2Zr-2Mo-0.25Si and Ti-6AL-2Sn-1.5Zr-1Mo-0.35Bi-0.1Si, which include both these metals and have relatively higher tensile strength and yield strength among alpha and near alpha titanium alloys. |
| Although no ANN models were constructed till date to predict the properties of α and near α-titanium alloys based on their composition, there are very few studies on the aspects such as kinetics of phase transformation of Ti– 6Al– 2Sn–4Zr–2Mo–0.08Si [7], Ti-6Al-2Zr-1Mo-1V [8] and Ti–8Al–1Mo–1V [9] alloys. |
 |
V. CONCLUSIONS |
| An ANN model has been suggested to evaluate and predict the properties of alpha and near alpha titanium alloys based on the composition and heat treatment parameters. The following conclusions can be drawn: |
| [1] The correlation coefficient (R) values are high corresponding to modulus of elasticity-torsional and electrical resistivity (1.00); reduction in area and hardness (0.99); thermal expansion (0.97); yield strength and modulus of elasticity-tensional (0.96); tensile strength (0.91); and percentage elongation (0.90). This suggests a very good correlation between the experimental and predicted valued by the ANN model |
| [2] Narrow mean absolute error and high prediction accuracy of various properties using ANN model suggests that ANN model is well trained and has excellent learning capability. |
| [3] Linear regression models (Y = mX + C) designed to study temperature-dependent changes in tensile strength, yield strength, percentage elongation and reduction in area are very good indices in understanding changes in the properties based on the composition using 'C' value while 'm' values are suggestive of temperature-dependent changes. |
| [4] 3D-structures were designed to study influence binary variables on tensile strength and yield strength. These models provided evidence that composition of Al, Si, Mo, Sn and Zr play a vital role in increasing tensile strength and yield strength to these alloys. |
References |
|