Keywords
|
| IT2FLC, Prediction, Polymer properties, Polymer Composites Properties, Effective Thermal Conductivity (ETC) |
INTRODUCTION
|
| The extrusion process is used for the production of commodities in diverse industrial sectors such as packaging, household, automotive, aerospace, marine, construction, electrical and electronic, and medical applications. Despite this success, it seems that effective thermal monitoring and control still remains an issue. Use of polymer materials has greatly increased over last few decades due to their many attractive properties such as ease of forming into complex shapes, lightweight with high tensile/impact/tear strengths, high temperature resistance, high chemical resistance, high clarity, reprocesseability and low cost. This has resulted in new industrial applications for polymer materials while enabling products to be more cost effective, flexible, and efficient. However, conventional technique is not efficient as the product quality is greatly affected by the flow history inside the extruder. Further complication includes the strong interactions between process parameters. For example, changes in the screw speed can lead to changes not only in the melt temperature, but in the flow rate as well. Consequently, a feasible control methodology shall consider the process as a multivariable and distributed parameter system. The design of an appropriate controller requires a dynamic model of the extrusion. In this paper, the interval type2 fuzzy rule-based system (IT2FFRBS)is applied as the models to approximate the operational-sensitive parameters. A brief description of the extrusion process is given, to be followed by soft computing applications in developing an IT2FLC model. The model evaluation is performed from the predictions on the melt temperature. Then, the usefulness of IT2FLC in approximating the operational-sensitive parameters is further investigated. |
| The extruder consists of a barrel, which is heated by a series of wall-mounted heater sand a rotating screw; the latter is linked to a gear system and a motor. Polymer particles are fed in through the hopper, by gravity into the helical screw channel. The screw has a varying channel depth along the axial direction. The melt flowing through the die is formed into an end product. Interval Type-2 Fuzzy logic controllers (IT2FLC’s) are one of useful control schemes for extrusion process having difficulties in deriving mathematical models or having performance limitations with conventional linear control schemes. Error e and change of error eÃâ¹Ã⢠are the most used interval type-2 fuzzy input variables, regardless of the complexity of controlled process. Also, either control input u (PD-type) or incremental control input Δu(PI-type) is typically used as a fuzzy output variable representing the rule consequent (“then” part of a rule). Most of the critical comments to fuzzy control are due to the lack of a general method for its stability analysis. But as Zadeh often points out, fuzzy control has been accepted by the fact that it is task-oriented control, while conventional control is characterized by set point oriented control, and hence do not need a mathematical analysis of stability. And as Sugeno says, in general, in most industrial applications, the stability of control is not fully guaranteed and the reliability of a control hardware system is considered to be more important than the stability. The success of fuzzy control, however, does not imply that we do not need a stability theory for it. Therefore, many researchers have worked to improve the performance of the IT2FLC’s and ensure their stability. Li and Gatland proposed a more systematic design method for PD and PI-type FLC’s. Choi, Kwak and Kim present a single-input FLC ensuring stability. Ying present a practical design method for nonlinear fuzzy controllers, and many other researchers have results on the matter of the stability of FLC’s. This work is based on Margaliotresults, we use the Margaliot criterion to built an Stable Type-2 Fuzzy Logic Controller for a Nonlinear Plant, in this case, the Inverted Pendulum. The same criterion can be used either linear or nonlinear plants/proesses. |
THE DEVELOPMENT OF DYNAMIC EXTRUSION MODEL
|
| An analytical dynamic model of the extrusion process is available. However, its application in the controller design is limited since it is not adaptive to the varying operating conditions. The variation could be due to the instability of the power supply affecting the screw speed and the barrel temperature, the changes of ambient conditions such as humidity, temperature, etc. In addition, the properties of the polymer to be processed may vary from batch to batch, depending on the regrind level, drying condition, etc.A number of process parameters are sensitive to the variation, particularly the polymer viscosity during the extrusion. The viscosity of melt is approximated by means of a power law model in the analytical model. |
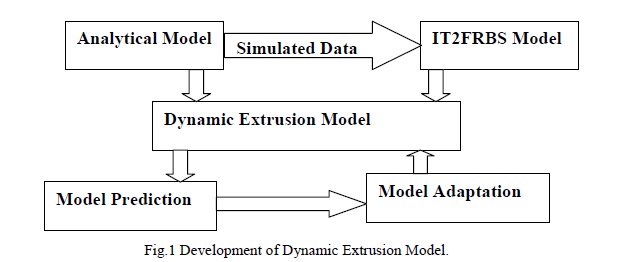 |
| The application of the power law model to describe the viscosity of melt has several shortcomings. In the present study, an extrusion model is developed by extending the analytical model so that the interval type-2 fuzzy rule-based system (IT2FRBS) is applied as a model to approximate the operational-sensitive parameters.Fig.1provides an overview of development of the semi-physical model for the extrusion process. The analytical model provides simulated data only for the initializations of the IT2FRBS model. The optimal sub-models thus obtained are incorporated into the analytical model forming the semi-physical model. The model is then simulated and the predictions are compared to the experimental measurements on the melt temperature. In existence of prediction error, a model adaptation algorithm will commence to minimize the error by tuning the parameters of the IT2FRBS model. The adaptation process is incorporated into the dynamic Extrusion model for further adaptation. The commencement of the adaptation process is dependent on the errors of the model predictions when compared with the actual melt temperature. The model adaptation is complicated since the adaptation process approximates only the operational-sensitive parameters but not directly the melt temperature. |
Polymer extrusion process
|
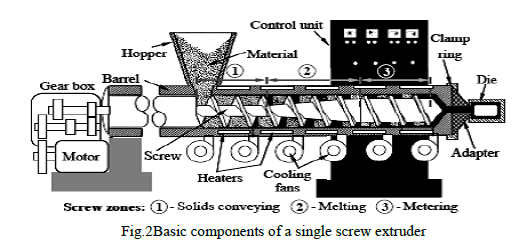
| There are two basic types of polymer processing extruders known as continuous and batch extruders (Rosato, 1998).Of these, single screw continuous extruders are the most commonly used in the plastics industry (Spalding and Hyun, 2003). The basic components of a single screw extruder are shown in Figure 2. The screw is the key component and has been divided into three main functional/geometrical zones (i.e. solids conveying, melting and metering) based on their primary operations. The material fed into the machine through the hopper is conveyed along the screw while absorbing heat provided by the barrel heaters and through process mechanical work. Eventually, a molten flow of material is forced into the die which forms the material into the desired shape. More details of the mechanisms of polymer extrusion can be found in Rauwendaal (2001). |
 |
Extrusion melts thermal control
|
| In polymer processing, melt temperature is one of the most important process variables and even small variations can cause poor product quality (Dormeier and Panreck, 1990). Under poor thermal conditions, several processing problems can occur, e.g. thermal degradation, output surging, poor mechanical properties, dimensional in stability, poor surface finish and poor optical clarity (Rauwendaal, 2001; Maddock, 1964; Fenner, 1979). Diemelt temperature homogeneity depends on the selection of processing conditions, machine geometry, and material properties (Brown et al., 2004b; Kelly et al., 2006;A beykoon et al., 2010b,a). Moreover, it has been found that melt temperature non-homogeneity increases with screw speed. Therefore, it is a challenging task to run extruders at higher screw speeds although the process energy efficiency then increases (Abeykoon et al., 2010c).An ideal controller would minimize poor thermal conditions such as melt flow non-homogeneity and achieve the highest possible thermal and energy efficiencies enabling the extruder to run at high speeds. Varying degrees of success have been achieved in the area of extrusion melt thermal control by manipulation of barrel temperature and screw speed settings using empirical modeling techniques. The majority of schemes have been concentrated on transfer function models mostly in combination with proportionalintegral- derivative (PID) approaches (Fingerle, 1978; Muhrer et al., 1983; Previdiet al., 2006). Some other work has used linear time-series regression techniques in process disturbances rejection and melt temperature control (Parna by et al., 1975; Kochhrand Parnaby, 1977; Hassn and Parnaby, 1981; Pattersonand Kerf, 1978; Costin et al., 1982; Germuska et al., 1984;Lin and Lee, 1997). Mercure and Trainor (1989) proposed time dependent partial differential equations to formulate a first principle mathematical model for the extruder barrel temperature control. |
INTERVAL TYPE-2 FUZZY LOGIC CONTROLLERS
|
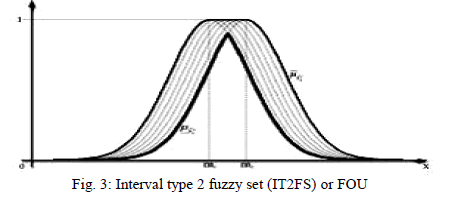
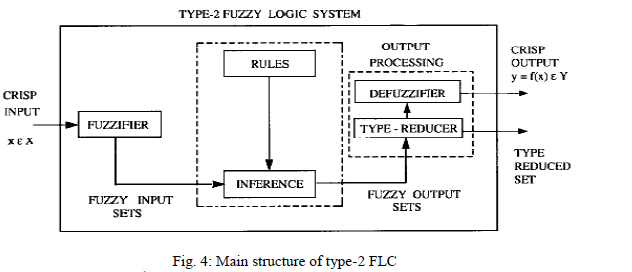
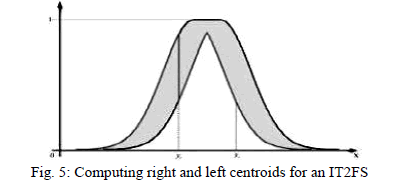
| Fuzzy Logic Controllers (FLCs) are known as the universal-approximates and have various applications in identification and control designs. A type-1 fuzzy Controller consists of four major parts: fuzzifier, rule base, inference engine and defuzzifier. A type-2 fuzzy Controller has a similar structure, but one of the major differences can be seen in the rule base part, where a type-2 rule base has antecedents and consequents using Type-2 Fuzzy Sets (T2FS). In a T2FS, we consider a Gaussian function with a known standard deviation, while the mean (m) varies between m1 and m2. Therefore, a uniform weighting is assumed to represent a footprint of uncertainty as shaded in Fig. 3. Because of using such a uniform weighting, we name the T2FS as an Interval Type-2 Fuzzy Set (IT2FS) also called Foot Print of Uncertainty (FOU). Utilizing a rule base which consists of IT2FSs, the output of the inference engine will also be a T2FS and hence we need a type-reducer to convert it to a type-1 fuzzy set before defuzzification can be carried out. Figure 4 shows the main structure of type-2 Fuzzy logic Controller (IT2FLC). |
| By using singleton fuzzification, the singleton inputs are fed into the inference engine. Combining the fuzzy if-then rules, the inference engine maps the singleton input x = [x1, x2,…x3] into a type-2 fuzzy set as the output. A typical form of an if-then rule can be written as: |
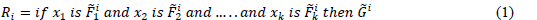 |
 |
 |
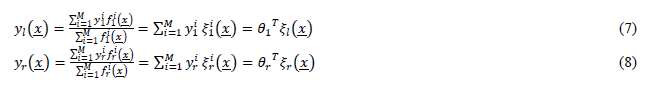 |
 |
 |
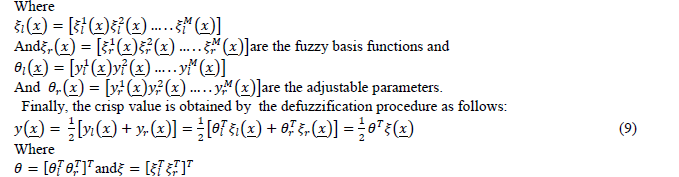 |
| Interval type-2 fuzzy set is used to model uncertainty and imprecision in a better way. Interval type2 fuzzy set is introduced at the first time at 1975 by Zadeh and developed by Mendel with characterizing interval type2 fuzzy set as Footprint of Uncertainty (FOU). FOU is limited by superior (Upper) and inferior(Lower)type-1 membership function. The development of fuzzy set from type1 to interval type2 in most cases always shows a better result. In order to control the polymer extrusion process, Interval Type2 Fuzzy Logic Controller (IT2FLC) is proposed. |
Input Membership Function
|
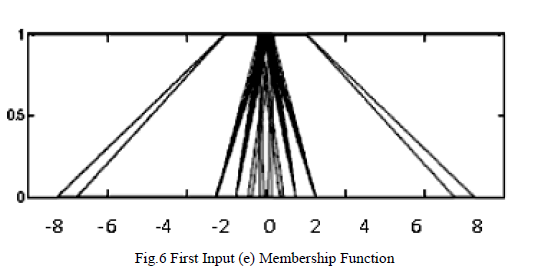
| Each of input variables e (error)& de(change in error) are classified by Input membership function consists of trapezoidal membership function and triangular membership function, described in Fig. 6. |
 |
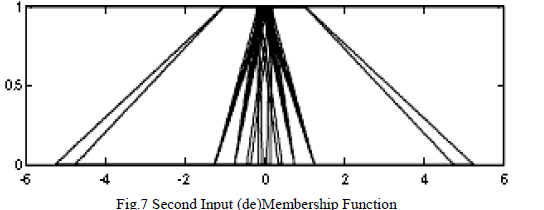 |
| The linguistic variable of first & second input memberships are shown in Fig. 6 and 7 can be described as follows: |

|
 |
 |
Rule Base
|
| Then the rule base can be developed by relating each value of e, change in e (de) and UController to its maximum membership class and IF – THEN rules are developed. |
| The rule1 is obtained as below |
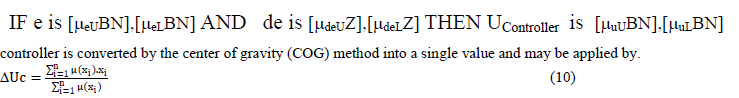 |
APPLICATIONS OF IT2FLC IN EXTRUSION THERMAL CONTROLIT2FLC CONTROLLER MODEL
|
| For the development of the melt temperature controller, five process inputs (i.e. screw speed and four barrel zone temperatures) were used as the manipulated variables. Two fuzzy logic controllers (named as IT2FLC 1 and IT2FLC2) provide the required control commands to these process inputs to reduce the die melt temperature variations across the melt flow while achieving desired average die melt temperature. Three error signals (i.e. the melt temperature variance error:e(Tv), the average die melt temperature error:e (Tm), and the mass throughput error:e (M)) are given as the inputs to the controllers and they make decisions to minimize these errors based on 50 knowledge-based linguistic if-then fuzzy rules (i.e. 31 rules for FLC1 and 19 rules for FLC 2). Errors are determined by the following equations. |
 |
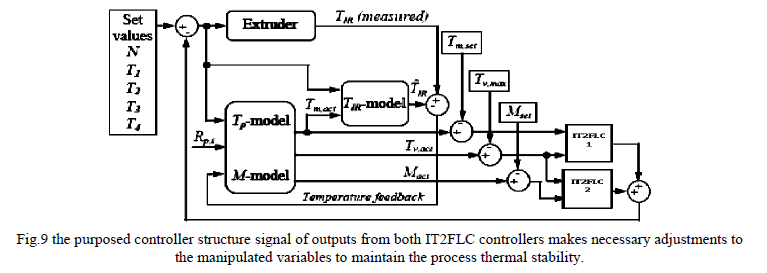
| Where Tv,act is the actual melt temperature variance, Tv,max is the maximum allowable melt temperature variance, Mact and Mset are the actual and set mass through-put rates, Tm,act and Tm,set are the actual and set average die melt temperatures. In practice, it is very difficult to measure a die melt temperature profile without disturbing the melt flow and hence a specially developed nonlinear polynomial dynamic model (Tp-model) is used to predict the melt temperature profile. The actual average die melt temperature (Tm,act) at each speed was determined by taking the mean of the measured temperature profile. Also, the temperature profile prediction accuracy is corrected from an error generated by a measured (TIR) and a predicted (IR) IR sensor readings. The IR temperature prediction model (TIRmodel) takes six inputs for its prediction (i.e. N, Tm,act, T1, T2, T3 andT4) and the 2nd order 6 terms dynamic TIR-model. The proposed controller structure with all of these models and IR sensor feedback is shown in Figure 9. |
| Interval Type2 Fuzzy logic (IT2FLC) has been widely used in industrial control applications and is becoming increasingly popular in modern process control. Taur et al. (1995) proposed a fuzzy PID temperature control for extruder barrel temperatures which exhibited good control capabilities. Tasi and Lu (1998) developed a single-loop fuzzy supervisory predictive PID controller also for extruder barrel temperature control. Recent work by Yusufet al. (2010) used fuzzy genetic algorithms in extruder barrel temperature control. In this work, an attempt was made to reduce die melt temperature variations across the melt while achieving desired average die melt temperature by manipulating the screw speed and barrel set temperatures. Feedback from an infrared (IR) temperature sensor was used to ensure the accuracy of temperature profile prediction. The control decisions were made by an interval type-2 fuzzy logic set of knowledge-based fuzzy rules. The work was focused on a single screw extruder which is the most common extrusion machine in industry. |
 |
Controlling Melt Temperature
|
| A main objective of controlling melt temperature is to develop a thermal control framework based on temperature profile measurements, which manipulates screw speed and individual set temperatures together to reduce undesirable melt temperature variations while maintain the required average temperature levels. Obviously, this type of controller will have to handle the complex nonlinear behaviors of the process. This study uses a model-based control approach and hence the performance of the controller depends on the accuracy of models. In this type of work, use of a control technique like interval type-2 fuzzy logic (IT2FLC) may be advantageous as it does not require fully accurate models. Another major advantage is that interval type2 fuzzy logic (IT2FLC) controller can handle process nonlinearities with a set of linguistic IF-THEN rules which do not require exact numerical boundaries. Due to these and its other advantages, interval type2 fuzzy logic (IT2FLC) was selected as the control technique for this study. |
THE MODEL SIMULATION
|
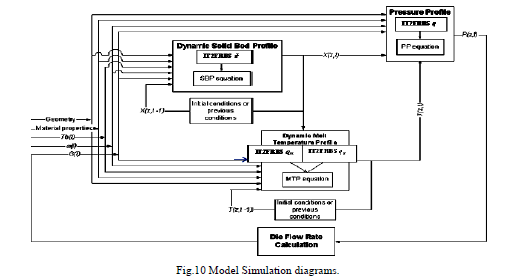
| Fig.10 illustrates the simulation path of the extrusion model. The program is initially provided with the following input data:a).Geometry parameters such as channel depth; b). Material properties such as density of solid polymer; c).Settings of screw speed ω (t) and barrel temperatureTb (t) as a function of time; d). Initial profiles at time t0 for the solid bed, X (z, t0)and the melt temperature T (z, t0);e).Location where the melting process commences; f).initial estimation of the output flow rate, G (t0). |
| The output flow rate G is initialized with the flow rate taken from the previous steady-state condition. When the operating condition changes with time, the program is iterated until a new steady-state condition is reached. The estimation on the output flow rate improves during the iteration. The relationship between flow rate and pressure-drop at the die ΔPdie is: |
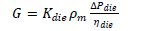 (14) (14) |
| Where Kdie and ρm are the die constant and the density of melt, respectively, while ηdie is the apparent viscosity of the melt at the die. |
| WhereX is the solid bed width and T is the melt temperature;φ is the melting coefficient; qtr is the heat transfer rate through barrel wall and qvc is the viscous dissipation rate. The process parameters that are sensitive to the operating conditions are φand qvc. Similar concern is applied for qtr due to the uncertainty in the heat transfer duration. These parameters have been expressed in the analytical model as the following functions: |
 |
| Where ω is the screw speed, Tb is the barrel temperature,G is the total mass flow rate, α is a set of parameters specifying the physical properties of polymer and the geometry of the extruder including the viscosity of melt η. The value of η is expressed by the power law model with reference to the local melt temperature and a set of coefficients θ. where θ is the coefficient set predetermined by the offline experiments on a rheometer. The deterministic equations (Eqs.(15)-(18)) used in the analytical model to approximate those varying operational-sensitive parameters are considered inappropriate, since they are not adaptive when the actual parameters are varying. The IT2FRBS is introduced as an alternative to describe the behaviors of those parameters. |
The model evaluation
|
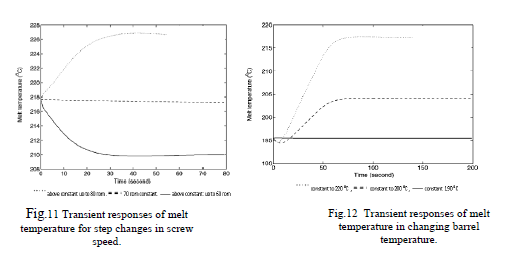
| Evaluation of the developed model is performed by first checking the consistency of the model prediction with the theoretical analysis. The model is simulated when step changes in the screw speed and the barrel temperature are applied separately. Fig.11showthe response of the temperature at the die when the screw speed is changed. The dashed lines represent the steady-state responses of the process; the dotted lines denote the responses of the system to a positive step change, whereas the solid lines are the responses to a negative step change. The model is also evaluated for an ideal case of altering the melt temperature at the die by manipulating the barrel temperature; assuming that step changes in the barrel temperature can be achieved in practice. The barrel temperature settings are indicated in the legend of Fig. 12. |
 |
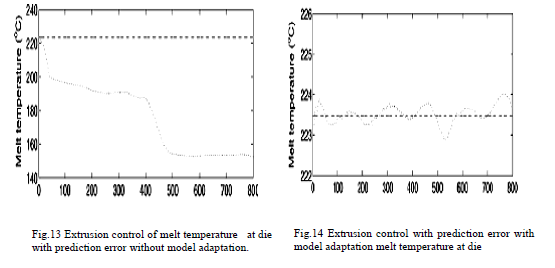
| The model predicts an increase in the melt temperature when the barrel temperature is set to a higher value. The higher barrel temperature results in more heat energy being transferred from the barrel wall to melt the solid polymer. Consequently, the melting mechanism commences earlier and the solid is completely melted sooner than the case where lower barrel temperature is applied. The model has been tuned automatically to approximate the operationalsensitive parameters in the new operating environment. The model is further evaluated when it is employed as the predictive model in the control Scheme namely as the interval type-2 fuzzy logic controller (IT2FLC). Fig.13indicates that without the adaptation, both of the plant outputs at die diverge if the prediction error exists. When the model adaptation commences, specifically when the approximations of the models have been tuned automatically according to the varying operating conditions, the melt temperature is regulated within tolerances as shown in Fig.14,respectively. |
 |
 |
RESULT AND DISCUSSION
|
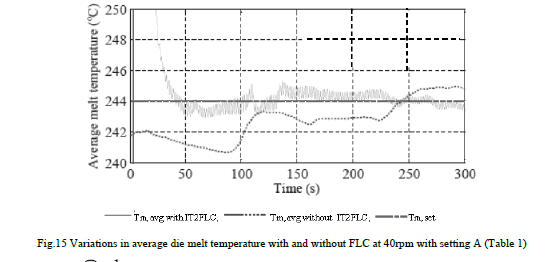
| The IT2FLC controller was implemented in MATLABSIMULINK to check its performance on a set of unseen data. All fuzzy rules were formulated by studying the experimental results and they were implemented by using triangular shaped membership functions. The Mamdani inference method (i.e. also known as a singleton output) was used with centre of area (i.e. centroid) fuzzification technique to construct the controller (Mamdani and Assilian, 1975). Measured vales of screw speed, barrel set temperatures and IR temperature was used as inputs to the controller. The set values of the average die melt temperature (i.e. by taking the average of measured die melt temperature profiles) and the mass throughput at each speed were determined from experimental results. The maximum allowable melt temperature variance was set as zero to achieve the minimum possible melt temperature fluctuations. The controller performance of achieving desired average die melt temperature is shown in Fig. 15. |
 |
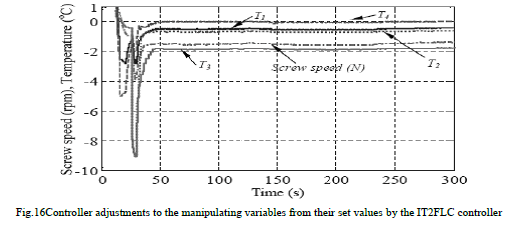 |
| Adjustments made by the IT2FLC controller (i.e. combined outputs from both IT2FLC1 and IT2FLC2 for each manipulating variable) to each process variables to achieve above results are shown in Figure 16.The experimental extruder was not instrumented with any melt temperature controller and only PID controllers were available to maintain each barrel set temperature in its set value. However, simulation results show that the proposed controller makes necessary changes to the screw speed and all barrel zone temperatures to maintain the desired average melt temperature while minimizing the melt temperature variance across the melt flow. The barrier flighted screw geometry used in these experiments seems to give good melting conditions in comparison to the conventional gradual compression screw geometry. The authors observed relatively larger melt temperature variances with a gradual compression screw geometry(the screw geometry most commonly used in industry)and temperature fluctuations increased as screw speed increased (Abeykoon et al., 2010a). |
CONCLUSION
|
| The paper highlighted some of the problems associated with the polymer extrusion modeling for real time control applications. A dynamic model has been developed to estimate the melt temperature and the pressure at the die. These parameters are regarded as the quality indicators of the extrusion operation. Interval type2 fuzzy rule-based (IT2FRB) model is applied as a means to capture the non-linearity characteristics of the operational-sensitive parameters. An interval type-2 fuzzy logic (IT2FLC) control framework to achieve the desired average die melt temperature was proposed and the simulation results confirmed its efficacy. The controller determines the average melt temperature based on a radial temperature profile of the die melt flow rather than a point-based measurement which is less accurate although common in practice. It is shown that interval type2 fuzzy rules based controller (IT2FRBC) provide good control capabilities to maintain the melt temperature homogeneity within desired limits by manipulating screw speed and barrel set temperatures in parallel. The controller performances can be further improved by improving the models accuracies, adding more fuzzy rules etc. Therefore, this may offer a new method to operate extruders at high screw speeds whilst achieving both high energy and thermal efficiencies. |
References
|
- C.Abeykoon, Li. M.McAfee, A.L.K. Kelly, E.C.Brown, (2010). “Monitoring the effect of operating conditions on melt temperaturehomogeneity in single-screwextrusion”. SPE ANTEC Tech. papers, 1799–1806.
- E.C.Brown, A. L.Kelly, P.D.Coates, (2004)“Melttemperature field measurement in single screw extrusionusing thermocouple meshes”. Review of Scientific Instruments 75 (11), 4742–4748.
- E. C.Brown, A. L.Kelly, P. D.Coates, (2004b). “Melt temperature homogeneity in single screw extrusion: effect of material type and screw geometry”. SPE ANTEC Tech. papers, 183–187.
- S.Dormeier, K. Panreck, (1990) “Dynamic behavior of the temperature during extrusion”.KunststoffeGermanPlastics 80 (11), 32–33.
- M.F.A.Fileti, A.J.B.Antunes, F.V.Silva,Silveira, V.Pereira, J. A. F. R., (2007). “Experimental investigationson fuzzy logic for process control”. Control Eng. Pract.15, 1149–1160.
- D.D. Germuska, P.A.Taylor, J. D. Wright, (1984) “Adaptive and multivariable control of a single screwextrusion system”. Can. J. Chem. Eng. 62, 790–801.
- A.L.Kelly, E.C. Brown, P.D. Coates, (2006)“The effect of screw geometry on melt temperature profile in singlescrew extrusion”. Polym. Eng. Sci. 46 (12), 1706–1714.
- J. J. Lin, G.Lee, (1997) “System identification for state feedback integral observer control of polymer plasticextrusion”. Polym.Plast. Technol. Eng. 36 (5), 749–775.
- I.Patterson, T.D.Kerf, (1978) “The dynamic behavior of extruders”. SPE ANTEC Tech. papers, 483–487.
- F.Previdi, S.M. Savaresi, A.Panarotto, (2006). Design of a feedback control system for real-time control of flow ina single-screw extruder. Control Eng. Pract. 14, 1111–1121.
- X.Shen, R.Malloy, J.Pacini, (1992)“An experimental evaluation of melt tempearture sensors for thermoplastic extrusion”. SPE ANTEC Tech. papers, 918–926.
- M.A. Spalding, K.S.Hyun, (2003). “Troubleshooting mixing problems in single-screw extruders”. SPE ANTEC Tech. papers, pp. 229–233.
- C.C.Tasi, C.H.Lu, (1998)“Fuzzy supervisory predictive PID control of a plastics extruder barrel”. J. Chin. Inst.Eng, 21 (5), 619–624.
- J.S.Taur, C.W. Tao, C.C.Tasi, (1995)“Temperature control of a plastic extrusion barrel using PID fuzzy controllers”. Int. IEEE/IAS conf. on Industrial automation and emerging technologies - Taiwan, 370–375.
- I.Yusuf, N.Iksan, N.S.Herman (2010)“A temperature control for plastic extruder used fuzzy genetic algorithms”. IMECS 2010-Hong Kong 2.
- B. Yang, L. J Lee, (1986) “Process control of polymer extrusion”. PartI. Feedback control, Polym. Eng. Sci. 26 (3), 197–204.
- S.H. Chiu, S.H. Pong, (1999) “In-line viscosity control in an extrusion process with a fuzzy gain scheduled PID controller”, J. Appl.Polym. Sci. 74, 541–555.
- L.P. Tan, A. Lotfi, E. Lai, (2002) “Hybrid soft computing methods in semi-physical polymer extrusion model identification”, in: Proceedings of the 2nd European Symposium on Intelligent Technologies, pp. 652–656.
- O. Cordon, F. Herrera, F. Hoffmann, L. Magdalena, (2001) “Genetic Fuzzy Systems: Evolutionary Tuning and Learning of Fuzzy Knowledge Base”, World Scientific Publishing, Singapore.
- H. Surmann, A. Selenschtschikow, (2002) “Automatic generation of fuzzy logic rule bases: examples (I)”, in: Proceedings of the NF, 2002, pp. 75–81.
- L.P. Tan, A. Lotfi, E. Lai, J.B. Hull, (2003) “Development and application of a fuzzy supervisory indirect learning control”,in: Proceedings of the 3rd European Symposium on Intelligent Technologies, pp. 346–352.
|