ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Roshan Dsouza1, Praveen M P2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this present study, a methodology is developed to estimate the fatigue life of the structure from acquired strain data for variable amplitude loading condition. The methodology is based on the nominal stress method and the method is used creating a software module. Rainflow cycle counting method is use to extract the cycles from the strain data. Then the Palmgren-Rule is utilized to calculate cumulative damage. In addition, the fatigue life of a cantilever aluminium plate under certain loading conditions is analysed. The results are compared with the professional fatigue analysis software "N-SOFT FATIMAS".
Keywords |
| Fatigue, Stress Life, Variable Amplitude Loading, Life Estimation, Palmgren-miner Rule |
I. INTRODUCTION |
| Fatigue is the process of progressive localized permanent structural change occurring in a material subjected to conditions that produce fluctuating stresses and strains at some point or points and that may culminate in cracks or complete fracture after a sufficient number of fluctuations. Fatigue life estimates are often needed in engineering design, specifically in analysing trial designs to ensure resistance to cracking. A similar need exists in the troubleshooting of cracking problems that appear in prototypes or service models of machines, vehicles, and structures. That is the reason that the predictive techniques are employed for applications ranging from initial sizing through prototype development and product verification.The failure analysis, prediction, and prevention are of critical importance to the designer to achieve a success. Fatigue design is one of the observed modes of mechanical failure in practice. For this reason, fatigue becomes an obvious design consideration for many structures, such as aircraft, bridges, railroad cars, automotive suspensions and vehicle frames. |
II. METHEDOLOGY |
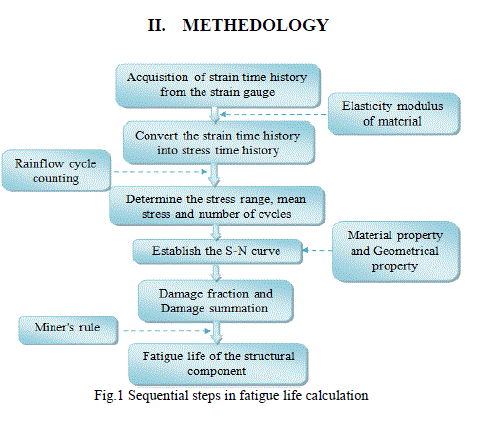 |
| The algorithm of this study is explained in the Fig.1. |
| The data acquisition instrument used to acquire the strain from the strain gauge mounted on required location in the structure. The strain-time data has been collected during the test is shown in the Fig.2. |
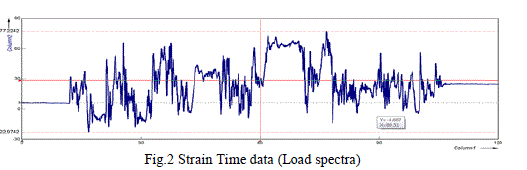 |
| The obtained strain-time data is converted into stress-time data by using the following equation: Stress-strain relationships |
| σ = E × ε |
| Rainflow cycles are counted by using computer programs. For lengthy histories, the range and mean values are often rounded off to discrete values in a range-mean matrix. |
| Using Modified Goodman Equation: |
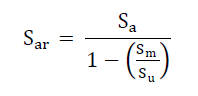 |
| Where |
| Sa = Alternating Stress Amplitude |
| Sm = Mean Stress value |
| Su = Ultimate tensile strength |
| Su = Ultimate tensile strength |
Geometrical Details at Strain gauge Location: |
| Modification Factor for Se: |
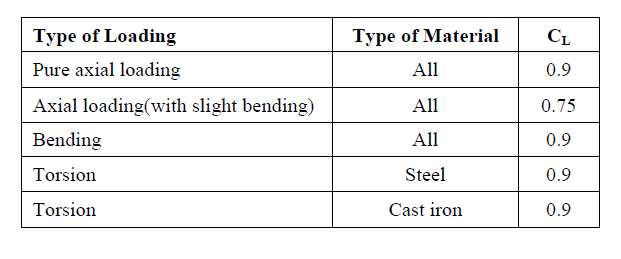
| 1. Loading Factor CL: |
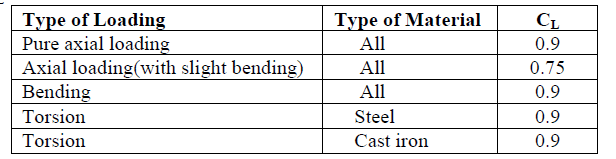 |
| 2. Surface finish CS: |
| High strength steels are more adversely affected by a rough surface finish than softer steels, for this reason the surface correction factor, CS, is strongly related to tensile strength. The surface finish correction factor is often presented on diagrams that categorize finish by means of qualitative terms such as polished, machined or forged. See Fig.3 |
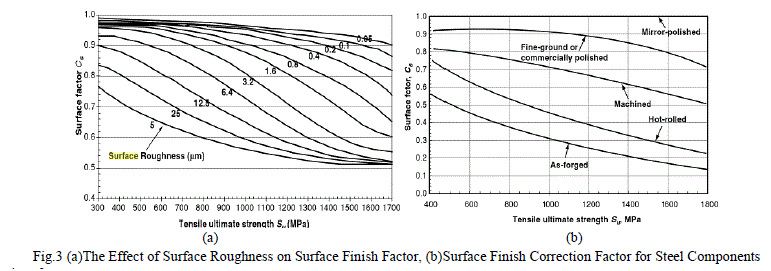 |
| Fig.3 (a)The Effect of Surface Roughness on Surface Finish Factor, (b)Surface Finish Correction Factor for Steel Components |
| 3. Size factor CD: |
| If the diameter of the shaft is < 8mm: |
| CD = 1 |
| If the diameter is between 8 mm and 250 mm: |
| CD = 1.189d−0.097 |
| For situations where components do not have a round cross section, an equivalent diameter, deq, can be calculated for a rectangular section width, w and thickness, t, undergoing bending from: |
| deq 2 = 0.65 × w × t |
| 4. Reliability Factor CR: |
| Using the standard normal cumulative distribution and assuming an 8 % standard deviation for both the stress and strength, an analytic expression for CR is deduced. |
| CR = 1 − 0.08Zr |
| Where Zr is the standard normal variable (defines the area under the normal distribution based on number of standard deviations from the mean). |
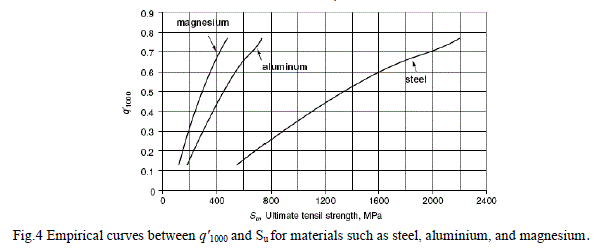
| 5. Notch Correction Factor Kf : |
| Kf = 1 + (Kt − 1) × q |
| Notch Sensitivity Factor |
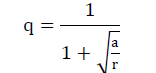 |
| Where ‘a’ is the Neuber's material constant related to the grain size and‘r’ is the notch root radius. |
Stress at Fatigue limit |
| WhereSbe = Baseline fatigue limit |
Modification Factor for S10 3: |
| 1. Loading Factor CL: |
 |
| 2. Reliability Factor CR: |
| Using the standard normal cumulative distribution and assuming an 8 % standard deviation for both the stress and strength, an analytic expression for CR is deduced |
| CR = 1 − 0.08Zr |
| Where Zr is the standard normal variable (defines the area under the normal distribution based on number of standard deviations from the mean). |
| 3. Notch Factor At 1000cycles: |
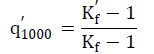 |
 |
Stress at 103 Cycles S10 3: |
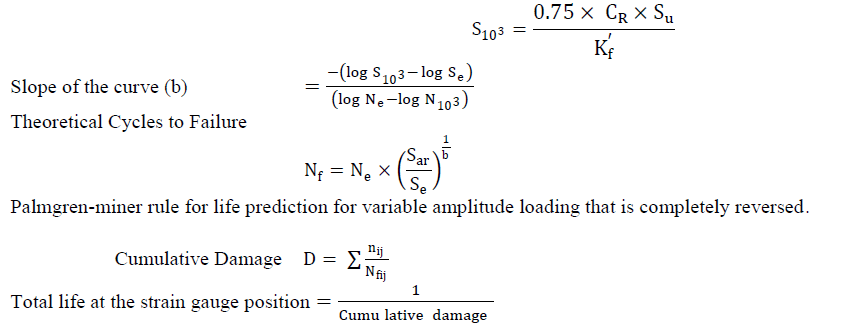 |
III. SOFTWARE DEVELOPMENT |
| The calculation whichever employed in this chapter are used in the development of the fatigue life analysis software. The Main Screen contains all main features fatigue analysis including the disply option of graps and plots in one single window. In the Main Screen the data entering options are located in the left side of the screen and Disply configuration on the centre of the screen and Results are displyed at the bottom. |
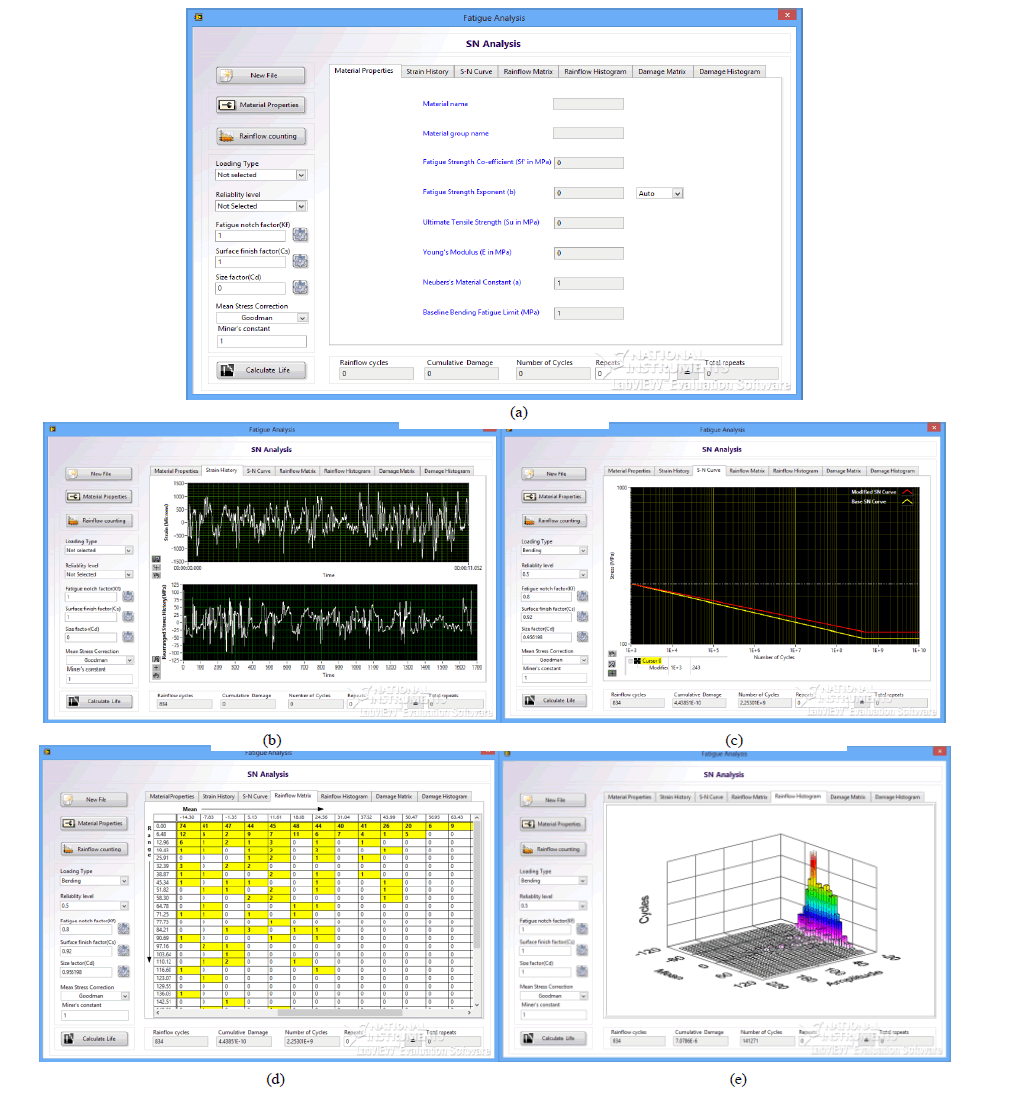 |
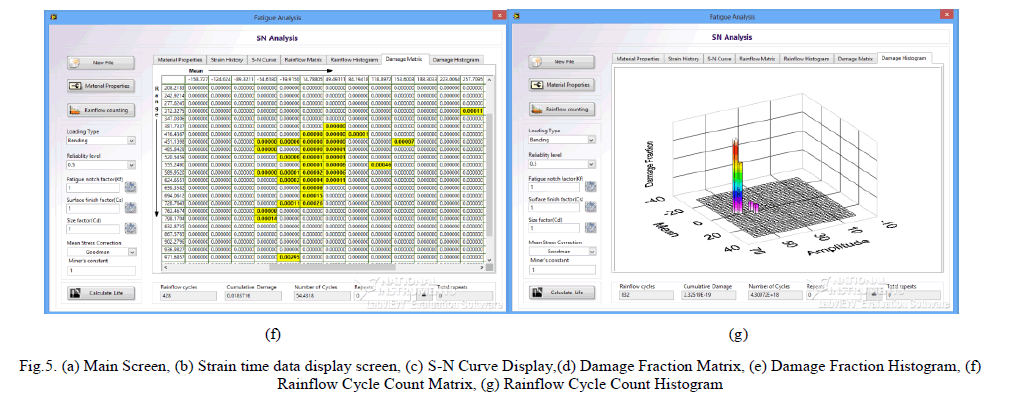 |
IV. VALIDATION OF THE METHOD |
| VALIDATION 1: Fatigue life of the eight sample strain histories are estimated using the current developed fatigue analysis software and "N-SOFT FATIMAS". The results are then comparing with results of "N-SOFT FATIMAS" for eight test sample signal. |
| VALIDATION 2: By Conducting Experiment, a cantilever aluminium plate under certain loading conditions is used as a test specimen. The fatigue behaviour of the test specimen subjected to constant loading is investigated experimentally. The acquired experimental data are then analysed using software. The strain gauge is glued on a critical point at the specimen where stress concentration exists in order to examine the life profile simulation. |
V. RESULTS AND DISCUSSIONS |
| The Rainflow cycle counts for all sample signals are equal in both software hence we can conclude that the Rainflow cycle counting method used in this developed software is matches with n-soft. The results obtained from the four cases(Fig.6) shows that the fatigue analysis method is nearly matches with n-soft. |
 |
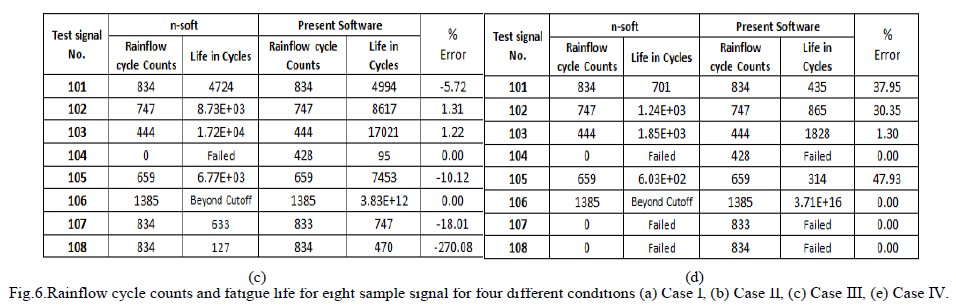 |
| The Rainflow cycle counts are unequal in the both software because the both software uses different signal filters. The life cycles obtained from the both the software are does not match experimental cycles hence the conducted experiment failed to validated software. The reasons for the failure of experimental method are yet to be analysed. |
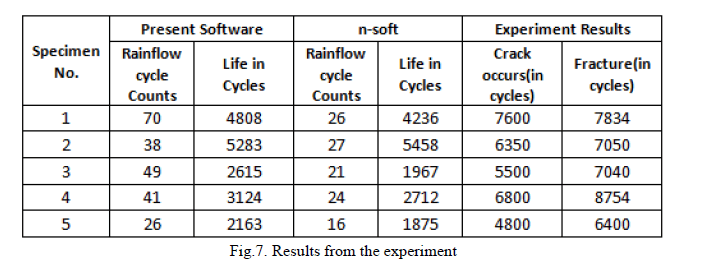 |
VI. CONCLUSION |
| The present work illustrates development of fatigue analysis software based on the nominal stress method. From the study it is known that the fatigue life of the any structure is depending on the material property, geometrical definition of the required point in the structure. The estimation and selection of the factor are made easy by related graph in module from that the user can select point of curve for corresponding parameter so that the user can understand procedure of life estimation easily. The main feature of this software is the all main operations are provided in the one screen along with display of results. The results from the validation 1 (CASE I-IV) shows that the Rainflow cycle counting method is matches with the n-soft and the error of estimated fatigue life is within 20%. The results from validation 2 shows that the experiment is unable to justify the method developed and the reason for failure of experiment are yet to be identified. |
References |
|