ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
M.Subanya1, D. Helena Margaret2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A hybrid model is proposed in order to use the design of compensating semiconductor optical amplifiers (SOAs) nonlinearity by adjusting cavity dispersion in a SOA-fiber ring mode-locked laser. It is predicted that, once the cavity dispersion is correctly adjusted, the mode-locked pulses of 10 ps width will become distortion-free Gaussians, with their time-bandwidth product(TB)very close to the fundamental Gaussian limit(TB=1/2)using root mean-square definition. This effects related to band-pass filter are shown as well. Our results highlight the ambiguity of TB using full-width at half-maximum (FWHM) definition. As result, the generally adopted concept of transform-limited pulse in its FWHM description may be misleading. Keywords- Optical pulses, semiconductor fiber ring laser, transform-limited pulse, ultrafast optics, pulse generation.
INTRODUCTION |
| In dispersion management fiber losses are no longer a major limiting factor for optical communication systems. Indeed, modern light wave systems are often limited by the dispersive and non linear effects rather than fiber losses[1]. In some sense optical amplifiers solve the loss problem but, at the same time, worse the dispersion problem since, in contrast with electronic regenerators, an optical amplifier does not restore the amplified signal to its original state. As a result, dispersion-induced degradation of the transmitted signal accumulates over multiple amplifiers[2]. |
| The group velocity dispersion effects can be minimized using a narrow line width laser and operating close to the zero dispersion wavelength of the fiber. However it is not always practical to match the operating wavelength. An example is provided by the third generation global systems operating near 1.55 micrometer and using optical transmitters containing a distributed feedback laser[3]. |
| In recent years there has been a lot of work on dispersion compensating fibers (DCFs), which are being used extensively for upgrading the installed 1310nm optimized optical fiber links for operation at 1550nm[3]. In the following two sections, we will discuss the basic principle behind dispersion compensation, and the characteristics of dispersion compensating fibers (DCFs). In one approach the DCF supports a single mode but it is designed with a relatively small value of the fiber parameter[2]. Unfortunately DCF also exhibit relatively high losses because of increase in bending losses. In general DCF are designed such that increases with wavelength. The wavelength dependence of D place a important role for wavelength division multiplexed (WDM) systems[4]. |
| Ring lasers are composed of two beams of light of the same polarization travelling in opposite directions (counter-rotating) in a closed loop. Currently ring lasers are used most frequently as gyroscopes (ring laser gyroscope) in moving vessels like cars, ships, planes, and missiles. The world's largest ring lasers can detect details of the Earth's rotation[5]. Such large rings are also capable of extending scientific research in many new directions, including the detection of gravitational waves, Fresnel drag, Lense-Thirring effect, and quantum-electrodynamics effect[6]. In a rotating ring laser gyroscope, the two counterpropagating waves are slightly shifted in frequency and an interference pattern is observed, which is used to determine the rotational speed. The response to a rotation is a frequency difference between the two beams, which is proportional to the rotation rate of the ring laser (Sagnac effect). The difference can easily be measured. Generally however, any non reciprocity in the propagation between the two beams leads to a beat frequency[8]. |
EXPERIMENT |
| The optical signal is coming from the continuous wave distributed feedback laser to Polarization controller. Here Polarization controller is used to allow one to modify the polarization state of light. The polarization controller gives to the optical signal to Mach-Zehnder modulator while at the same time RF signal also gives to the MZ modulator. Here MZ modulator receive the two signal and convert to optical signal to the Erbium Doped Fiber Amplifier (EDFA). |
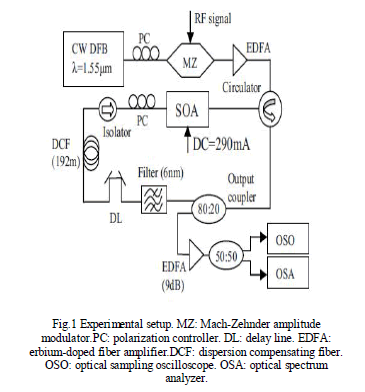 |
| Then after EDFA the optical signal gives to the Circulator (or) Coupler but here we are used to coupler. The coupler is used to combine and split signals in an optical network. A kind of laser mirror known as an output coupler. The signals are go to the output coupler. In pure optical signals 20% are go to the EDFA through coupler. Remaining signals are go to the Bessel Filter. Here Bessel filters work as a constant group delay across the entire passband. Next delay line here propagation delay, the length of time taken for something to reach its destination. After delay line here pulse broading can be created. The DCF compensates the dispersion that is being created. Here Isolator is a two port device that transmits the signals one direction only. This setup is created feedback through Ring Laser. In the SOA created nonlinearity by adjusting the cavity dispersion in a SOA fiber ring mode locked laser and 80% of the optical signals are combined to 20% of the remaining signals. It can be created the distortion free Gaussian pulse with their time-band width produce very close to the fundamental Gaussian limit. |
MODEL AND ALGORITHM |
| A. Hybrid Model |
| Recognizing that pulse width _t ≥ 6 ps in general in SOA-related lasers excluding external pulse compression, it is not necessary in the present model to include the effect of gain dispersion, since its time constant is ~0.1 ps [10]. Other ultrafast effects, notably two-photon absorption, are also neglected for the same reason and the fact that optical power level is moderate here. In this regime, the dominant physical effects inside SOA are carrier recovery and gain saturation. Assuming slowly-varying envelops, the electrical field in SOA is |
| E(z, t) = [A(z, t) exp(iβ0z) + B(z, t) exp(−iβ0z)] |
| ×exp(−iω0t). (1) |
| Here, A and B are the forward (+z) and the backward(−z) field envelops, β0 and ω0 are the freespace propagation constant and the carrier frequency, respectively. Lateral and polarization effects are ignored. Notice that the carrier frequencies for A and B are independent, but this makes no difference in the model. The propagation for A, B is described by [6], [7]: |
| ∂zA + v−1 g ∂t A = 1/2[g(1 − iαH) − αint] A (2) |
| −∂zB + v−1g ∂t B = 1/2[g(1 − iαH) − αint] B. (3) |
| Together with the rate equation for the optical gain g(z, t): |
| ∂tg = (g0 – g)/τ− (g(|A|2 + |B|2))/Esat. (4) |
| In the above equations, vg is the group velocity in SOA, αH is the Henry’s factor, αint is SOA’s internal loss coefficient, g0 is the small-signal optical gain, τ is the carrier lifetime, Esat is the saturation energy. The small-signal net gain is thus G0 = exp[(g0-αint)LSOA]. Due to a narrow frequency bandwidth involved, these parameters are assumed to be constant. Notice that the noise term is not explicitly present in (2)–(4), it will be included as an additional input afterward. The SOA’s output envelop (Aout in makes a roundtrip through the ring, and emerges as a renewed input Ain. The transmission of the pulse train in the fiber link of 200 m could be considered as linear, since with a peak intensity of mW, the nonlinear length LNL will be 50 km for a typical SMF [6]. Therefore, nonlinear effects in the fiber link are not a concern, even though relevant fiber parameters in our experiment differ from those in [9]. Consequently, the transmission through the fiber link could be described by a transfer function in the frequency domain |
| H(ω) =(á¾¹inN+1 (ω))/á¾¹Nout(ω) = η × exp[_−1/2(2 √ln 2 �� (ω − ω0) /BBP)4]× |
| exp [iβ2L(ω − ω0)2/2] . (5) |
| Here, ÃN+1 in and ÃN out are the frequency domain presentations of AN+1 in and AN out, respectively, with the integer N denoting the number of roundtrip; η is the total amplitude attenuation, including the loss from the output coupler; BBP is the band-pass filter’s 3 dB bandwidth, its flat-top form is checked by us and is well fitted by the first exponent above. For simplicity, we assume that the filter is centered at ω0. The consequence of this assumption will be discussed later. The second exponent depicts the effect of group velocity dispersion (GVD) in the fiber link, β2 is the GVD parameter averaged throughout the link, and L is the total length of the ring. In the following, we replace β2 by the dispersion parameter D through the relation D = −2πcβ2λ2, with λ = 1.55 μm. Higher-order dispersion is neglected due to relatively long pulse widths and the high value of β2 involved [10], inconsistency with the rest of the model. Some other components are also implicitly contained in (5). These include a polarization controller, whose attenuation is accounted for by η, and an optical delay for synchronization. It is assumed that harmonic modelocking is achieved, i.e., the roundtrip delay corresponds to an exact multiple of modulation period. This explains the absence of β1 (the inverse of the group velocity in the fiber) in (5). In effect, the optical delay in |
| Fig. 1 is already included in the total length L. Modelocking is achieved if with a big enough N (102), |AN+1 in| = |AN in|. The hybrid model is thus complete. |
SIMULATION AND ANALYSIS |
| Deployment of optical communication systems is costly and reconfiguration is in some cases impossible or not economical. Therefore experiments and simulation of systems are necessary to predict and optimize system performance. Optical communication systems today involve a very high degree of complexity. There is a growing need for optimization across the different layers of the communication system. In addition to that, laboratory equipment is expensive and in some cases components are not available from vendors at the beginning of the design process. Simulations are not affected by these problems because components can be described by parameters or by statistical properties |
OPTISYSTEM DESIGN SOFTWARE |
| OptiSystem, a simulation package by Optiwave Systems Inc., Ottawa, Canada. One of the main reasons for this decision is the clarity of the graphical user interface. The main features of OptiSystem are OptiSystem Component Library includes hundreds of validated components. Users may customize by entering parameters that can be measured from real devices. Integration with Optiwave software tools at the subsystem and component level: OptiAmplifier, OptiBPM, OptiGrating, and OptiFiber. Integration with ADS software from Agilent. OptiSystem handles mixed signal formats for optical and electrical signals in the Component Library, and calculates the signals using the appropriate algorithms related to the required simulation accuracy and efficiency. System performance is predicted by calculating BER and Q-Factor using numerical analysis or Semianalytical techniques for systems limited by inter symbol interference and noise. Advanced visualization tools produce OSA Spectra, Oscilloscope, and Eye diagrams. Also included are WDM analysis tools listing signal power, gain, noise figure, and OSNR. Simulations can be repeated with an iteration variation of the parameters.. |
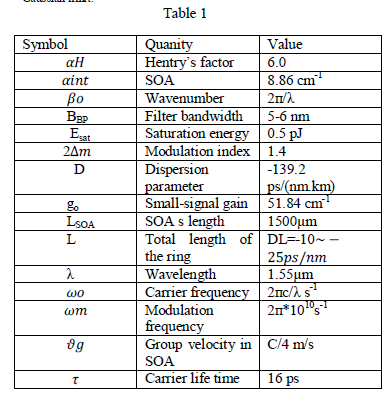
| The modulation and the filter functions are also measured and will be given in Section III. The parameters adopted are listed in Table 1. The average power of the extracted pulse train is ~0.3 Mw (with an average back injection power of ~9 mW), its spectral width is less than 1nm. This pulse train is first boosted by an EDFA with +9 dB gain. Compared to EDFA’s saturation power (~10 mW) and its amplification bandwidth (>35 nm) [8], the differences are 1 ~ 2 orders of magnitude for both values. Therefore, the pulse’s original shape and spectrum are preserved after EDFA. The amplified pulse train is then analyzed simultaneously by an optical sampling oscilloscope (OSO, Ando AQ7750), with its input bandwidth. table 1 parameters used in the simulation Symbol Quantity Value or Relation αH Henry’s factor 6.0 αint SOAs internal loss 8.86 cm−1 β0 Wave number 2π/λ BBP Filter bandwidth variable, 5−6 nm Esat SOAs saturation energy 0.5 pJ 2_m Modulation index 1.4 D Dispersion parameter −139.2 ps/(nm·km) for DCF (to be averaged with SMF) g0 Small-signal gain 51.84 cm−1 (G0 = 28 dB net gain) LSOA SOAs length 1500 μm L Total length of the ring variable (DL= −10 ~-25 ps/nm) λ Wavelength 1.55 μm ω0 Carrier frequency 2πc/λ s−1 (c = 3 × 108 m/s) ωm Modulation frequency 2π × 1010 s−1 vg Group velocity in SOA c/4 m/s τ Carrier lifetime 16 ps 25ps /div 2mW/div . Oscilloscope trace of the output pulse train. of 500 GHz and a resolution of 0.6 ps in time, and by an optical spectrum analyzer (OSA, Apex AP2440A), with its spectral resolution of 0.16 pm or 20 MHz between λ = 1520-1567 nm. The peak power in the ring cavity, just before the output coupler, is estimated to be ≈12 mW. The oscilloscope trace of the output pulse train is shown in Fig. 2. |
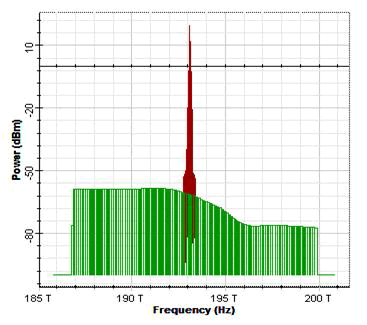 |
| Fig 2 |
| The spectrum analyzer view the final output of Gaussian pulse with their time band width product very close to the fundamental Gaussian limit. |
 |
CONCLUSION |
| The model presented in this paper demonstrates its capability of predicting and analyzing the behaviors of mode locked optical pulses in a SOA-fiber ring laser. The associated algorithm is shown to be accurate enough to address the questions asked at the beginning of the paper. |
| In the condition of adequate cavity dispersion, nearly perfect Gaussian pulses can be expected. Their timebandwidth product using RMS definition could be very close to the fundamental Gaussian limit. These pulses would have a slight and linear chirp as result of the dispersion management. Thanks to their narrow spectral widths, these pulses are resilient to parameter variations, including filter bandwidth change. If the cavity dispersion is not correctly adjusted, the cleanness of mode-locked pulses will degrade, as measured by their energy spreads in both time-and frequency domain. These pulses will then have rather complicated waveforms and spectra, and are consequently more sensitive to parameter variations. It is also demonstrated that this SOA-fiber ring laser does not support optical solutions. The method and arguments developed in this paper could be applied to other similar laser system using SOA as active devices |
References |
|