ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Nisha Barle, Rama Sarojinee, Manoj Kumar Jha
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Diagnosis techniques based on the dissolved gas analysis (DGA) have been developed to detect incipient faults in power transformers. Various methods exist based on DGA such as IEC, Roger, Dornenburg, and etc. However, these methods have been applied to different problems with different standards. Furthermore, it is difficult to achieve an accurate diagnosis by DGA without experienced experts. In order to resolve these drawbacks, this paper proposes a novel diagnosis method using Area Under Receiver Operating Characteristics Curve (AUROCC)-based Genetic Fuzzy SVM fusion model. Recently, the use of Receiver Operating Characteristic (ROC) Curve and the area under the ROC Curve called Area Under Receiver Operating Characteristics Curve (AUROCC) has been receiving much attention as a measure of the performance of machine learning algorithms. In this paper, we propose a SVM classifier fusion model using genetic fuzzy system. Genetic algorithms are applied to tune the optimal fuzzy membership functions. The performance of SVM classifiers are evaluated by their AUROCCs. Our experiments show that AUROCC-based genetic fuzzy SVM fusion model produces not only better AUROCC but also better accuracy than individual SVM classifiers
Keywords |
| Dissolved Gas Analysis, Area Under Receiver Operating Characteristics Curve (AUROCC), Support Vector Machines (SVMs), Genetic Fuzzy System (GFS), Classifier fusion |
INTRODUCTION |
| In extended power systems, substation facilities have become both too complex and too large. Customers require the high quality offered by an electrical power system. However, some facilities have become old and often break down unexpectedly. Such unexpected failure may cause a break in the power system and result in loss of profits. Therefore, it is important to prevent abrupt faults by monitoring the condition of power systems. Among the various power facilities, power transformers play an important role in transmission and distribution systems. At present, it has been proven that the dissolved gas analysis (DGA) is the most effective and convenient method to diagnose the transformers. Under normal conditions, the insulating oil and the organic insulating material in oil-filled equipment generate a small amount of gas caused by the gradual degradation and decomposition. The DGA approach identifies faults by considering the ratios of specific gas concentration. There are various methods based on DGA such as Dornenburg ratios, Roger ratios, IEC ratios, and etc. The DGA is a simple, inexpensive, and non-intrusive technique. The transformer oil provides both cooling and electrical insulation. It baths every internal component and contains a lot of diagnostic information in the form of dissolved gases. Since these gases reveal the faults of a transformer, they are known as Fault Gases. The DGA is the study of dissolved gases in transformer oil. The concentration of the different gases provides information about the type of incipient-fault condition present as well as the severity. Different methods Rogers, fuzzy, neural, key gas method, duval, dornenburg ratio etc. are available for fault detection using DGA data. |
| Under the abnormal condition in transformers, the insulation oil and the organic insulation material in oil filled equipment generate several gases such as hydrogen (H2), carbon monoxide (CO), acetylene (C2H2), methane (CH4), ethane (C2H6), ethylene (C2H4), carbon dioxide (CO2), and etc. The quantity of the dissolved gas depends fundamentally on the types of faults occurring within power transformers. By considering these characteristics, DGA methods make it possible to detect the abnormality of the transformers. |
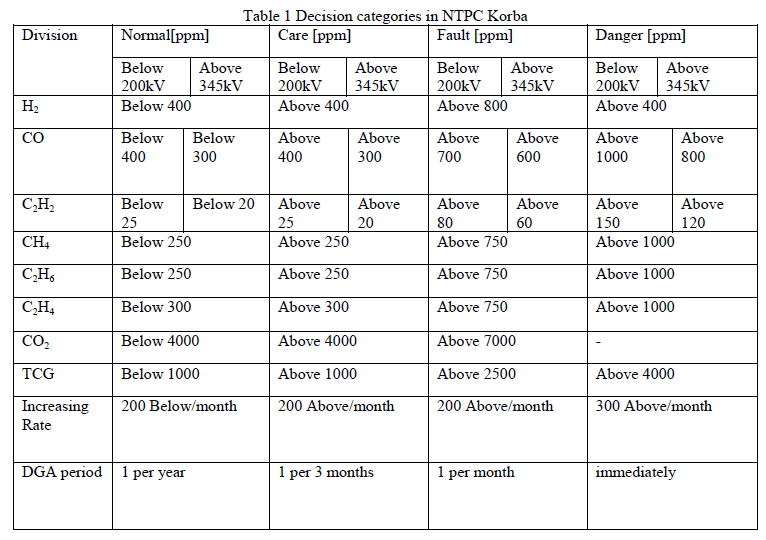
| Table 1 shows decision criteria according to quantity of each dissolved gas in transformers, which means the standard considered in NTPC Korba India (National Thermal Power Development Corporation Korba, India). More specifically, this method determines incipient faults in transformers according to the amount of gasses acquired from DGA. Here, the incipient faults include normal, alarm, fault, and danger. Also, this method makes it possible to identify the causes of faults represented as partial discharge, insulator degradation, arc discharge, low overheat and high overheat according to the concentration of special gasses. |
| This diagnosis technique based on these categories has certain limitations. For example, in case of exceeding 400 (ppm) for the concentration of hydrogen, this method determines the fault as an alarm condition and identifies the cause of the fault as partial discharges. However, the transformer is assumed to be operating normally in case of 399 (ppm). Even though the difference between the two data is only 1 (ppm), the interpretations are completely different. This indicates a very crisp interpretation with respect to the boundaries. |
| On the other hand, a specific gas is generated and accumulated in the oil as time goes on in spite of the normal condition. Therefore, the potential possibility and the degree of aging could be different even to transformers that are in normal condition. In fact, the amount of these gases indicates the potential for seeking a method for finding a faulted condition. This fault detection should be made periodically by means of DGA to maintain reliable operation of the transformers. Therefore, the variation of the existence and the concentration of the gasses with time must be taken into account for an accurate identification of the fault evolution and the aging reasons. |
 |
| The soft computing techniques like Fuzzy, Neural and Neuro-fuzzy utilizes limited parameters where as the parameters are not compressive, hence resulted into inaccurate classification of it. Support Vector Machines is a powerful methodology for solving problems in nonlinear classification. The advantage of DGA is that the operation and test are performed at the same time, in addition to the fact that it is a simple and inexpensive diagnosis process. However, much uncertainty exists in the data with respect to the dissolved gas. For example, the amount of special gas in normal condition could vary according to the characteristics of the transformer. Furthermore, the DGA method cannot provide accurate diagnosis without the help of experienced experts. |
| The proposed SVM classifiers are applied to solve the practical problems of small samples and non-linear prediction better and it is suitable for the DGA in power transformers. The accuracy of an SVM model is largely dependent on the selection of the model parameters. This paper uses genetic algorithm to optimize the parameters of AUROCC-based genetic fuzzy SVM fusion model. Genetic algorithm uses selection, crossover and mutation operation to search the model parameter. Classifier fusion is to combine a set of classifiers in a certain way so that the combined classifier can receive a better performance than its composing individual classifiers. The reason that the combined classifier could outperform the best individual classifier is because the data examples misclassified by the different classifiers would not necessarily overlap, which leaves the room for the classifier complementariness. A fuzzy logic system (FLS) is constructed to combine multiple SVM classifiers in the light of the performance of each individual classifier. The memberships of the fuzzy logic system are tuned by genetic algorithms (GAs) to generate the optimal fuzzy logic system. One question here is how to evaluate classifier performance in the fusion model. Typically, accuracy is the standard criterion to evaluate a classifier performance. The Receiver Operating Characteristics (ROC) and the area under an ROC curve (AUC) have been shown to be statistically consistent with and more discriminating than accuracy empirically and theoretically. This paper will use AUC as the evaluation of classifier performance to build the genetic fuzzy fusion model to enhance the performance of SVM classifiers. Then proposed method is applied to measure the possibility and degree of aging as well as the faults occurred in the transformer. To demonstrate the validity of the proposed method, various experiments are performed and their results are presented. To demonstrate the validity of the proposed method, an experiment is performed and its results are illustrated. The objective of this paper is to develop a AUROCC-based genetic fuzzy SVM fusion model and then this model is used for Dissolved Gas analysis (DGA) in power transformer. The results compare diagnostic performance according to normal, care and healthy conditions with respect to our method and expert’s decision are discussed. Also aging degree of power transformer for insulation degradation and CO2 excess for good, medium and low conditions are demonstrated. |
| In this paper while developing AUROCC-based genetic fuzzy SVM fusion model, we will first introduce the Proposed Diagnosis System using AUROCC-based genetic fuzzy SVM fusion model in Section 2. Then we will discuss Genetic Fuzzy SVM Fusion Based on AUROCC in Section 3. The Tuning Fuzzy System Using GA’s will be proposed in Section 4 and Experimental Result and Analysis will be discussed in Section 5. Finally in Section 6, conclusions will be drawn. |
PROPOSED DIAGNOSIS SYSTEM USING AUROCC-BASED GENETIC FUZZY SVM FUSION MODEL |
| The proposed diagnosis system is illustrated in Fig.1. It is shown that the system contains four modules, which are normalization, classification, model formation by AUROCC-based genetic fuzzy SVM classifier fusion, and diagnosis parts. To make reasonable DGA data, normalization needs to be considered. In this research, input data is normalized by a fuzzy membership function named a sigmoid function. This fuzzy function creates input data with nonlinear scale value ranged form 0 to 1. The normalized value is given by Eq.(1). Here, a and c are the slope and the center of the function, respectively. As seen in Eq. (1), we should set the two parameters (a, c) in advance. This normalization scheme can be expected to perform well if prior knowledge about data distribution among each decision criteria is available. These parameters are determined through the analysis of distribution and extensive experimentation. |
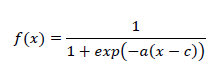 |
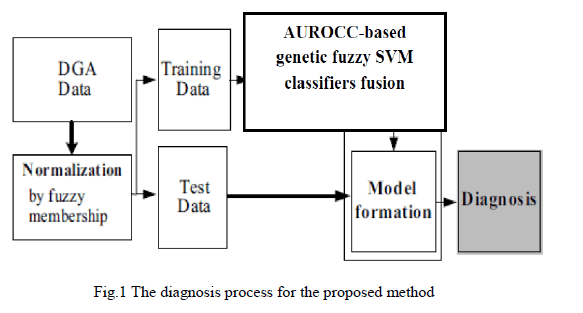 |
| As the next process, we propose a classifier fusion model particularly for SVM classifiers aiming to boost the performance of SVM classifiers. A fuzzy logic system (FLS) is constructed to combine multiple SVM classifiers in the light of the performance of each individual classifier. The memberships of the fuzzy logic system are tuned by genetic algorithms (GAs) to generate the optimal fuzzy logic system. Receiver Operating Characteristics (ROC) and the area under an ROC curve (AUROCC) have been shown to be statistically consistent with and more discriminating than accuracy empirically and theoretically. This paper will use AUC as the evaluation of classifier performance to build the genetic fuzzy fusion model to enhance the performance of SVM classifiers. It has also been shown that classifiers based on AUC produce not only better AUC, but also better accuracy. |
| Finally, the diagnosis is determined by selecting a class with the maximum value among the output layer in the AUROCC-based genetic fuzzy SVM fusion model. |
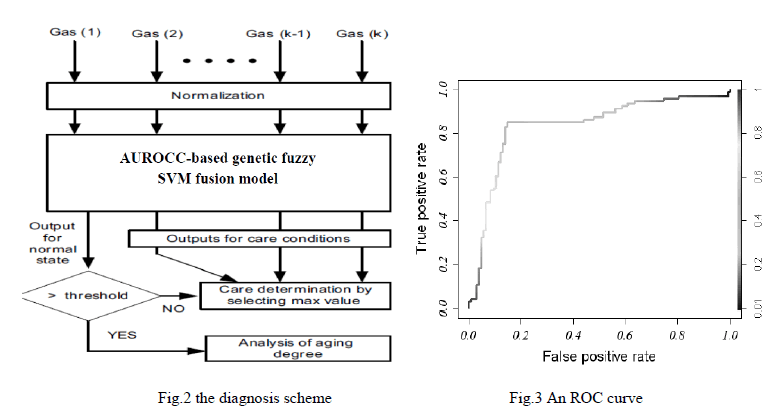
| Diagnosis scheme |
| Fig. 2 shows the diagnosis scheme proposed in this paper. Output nodes include normal state and various alarm conditions. As the first step in the determination of the state of the transformer, we consider the output value of normal condition. If this value is larger than the predefined threshold, we conclude that the transformer is normal; otherwise it is in care state. In case of normal state, we determine the aging degree according to the output values for normal state calculated by AUROCC-based genetic fuzzy SVM fusion model. In case of care state, diagnosis is performed by selecting the care condition with the maximum value among the output values of care conditions. |
 |
ROC Analysis for Binary Classification |
| ROC has been receiving much attention recently as a measure to analyze classifier performance and has attractive properties that make it especially useful for domains with skewed class distribution and unequal classification error costs. An ROC curve of a classifier is a plot of true positive rate (TPR) on Y axis versus false positive rate (FPR) on the X axis as shown in Fig.3. The TPR and FPR are defined as ïÿýïÿýïÿýïÿýïÿýïÿý = ïÿýïÿýïÿýïÿý ïÿýïÿý+ and Fïÿýïÿýïÿýïÿý = ïÿýïÿýïÿýïÿý ïÿýïÿý− where TP denotes true positives, FP denotes false positives, and N + and N – denote positives and negatives respectively. For a discrete classifier, which produces only a positive/negative class label on each example, only a single point can be drawn in the ROC graph. However, for a probabilistic classifier, which yields a numeric value on each example representing the degree to which an example belongs to a class, if various decision thresholds are applied to classify data examples, a series of points can be plotted in a ROC plane with pairs of {FPR, TPR} as their coordinates. Each threshold results in one point on the ROC curve representing the classifier which is generated by using this threshold as the cutoff point. Therefore, an ROC curve of a probabilistic classifier can be viewed as an aggregation of classifiers from all possible decision thresholds. The quality of an ROC curve can be summarized in one value by calculating the Area Under the ROC curve (AUROCC). AUROCC represents the probability that one classifier ranks a randomly chosen positive example higher than a randomly chosen negative example. According to Hand, AUROCC can be simply calculated in the following formula: |
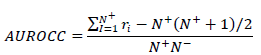 |
| Where ri denotes the rank of ith positive example in the ranking list if we arrange the classification results of data examples in ascending order. AUROCC been shown to be a better measure than accuracy when assessing classifier performances. |
GENETIC FUZZY SVM FUSION BASED ON AUROCC |
| When lack of human expert, rather than choosing fuzzy MFs or defining fuzzy rules in a manual trail-and-error manner, we may seek the assistant from a learning process. A genetic fuzzy system (GFS) is able to learn and search fuzzy MFs or fuzzy rules efficiently. It is basically a fuzzy system augmented by a learning process based on a genetic algorithm. GAs are able to learn or train or tune different components of fuzzy logic systems. |
| The genetic fuzzy fusion model for combing SVM classifiers is constructed as shown in Fig.4. The system has three phases. In phase I, training data are trained on different SVMs. Validation data are |
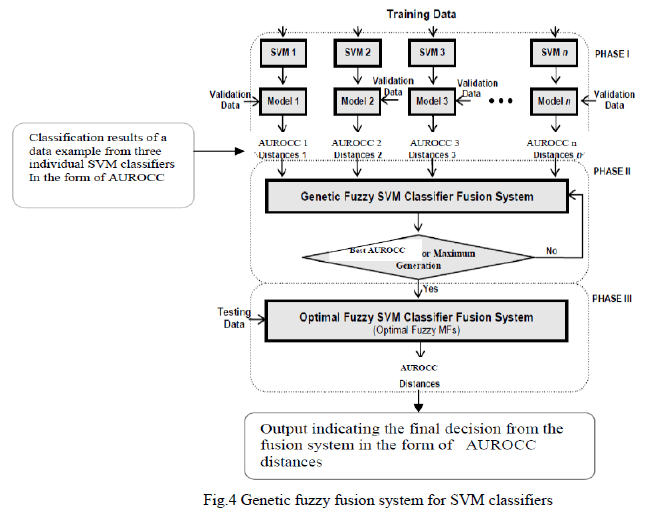 |
| classified to obtain individual SVM AUROCCs and distances of validation data examples to SVM hyperplanes. In phase II, a GFS is constructed and fuzzy MFs are tuned by GAs in cross validation manner. Finally, in phase III, testing data are fed into the optimal fuzzy fusion system to make the final decision. We have implemented the proposed fusion system on combing three SVM classifiers and will be used for DGA diagnosis in power transformer in the rest of the section. This process can be easily extended to combine arbitrary number of SVMs in general. |
| Fuzzy System Inputs and Output |
| The fuzzy fusion system is designed by applying Mamdani model where the consequences of fuzzy rules are fuzzy sets. In the fusion system combining three SVM classifiers, there are three AUROCC inputs depicting three SVM classifier performances, three distance inputs representing the classification results of a data example from three individual SVM classifiers, and one output indicating the final decision from the fusion system for the example. All the MFs of the inputs and output are defined as simple triangles shown in Fig.5. Each AUROCC input is described by two fuzzy sets: low and high, and each distance input is also represented by two |
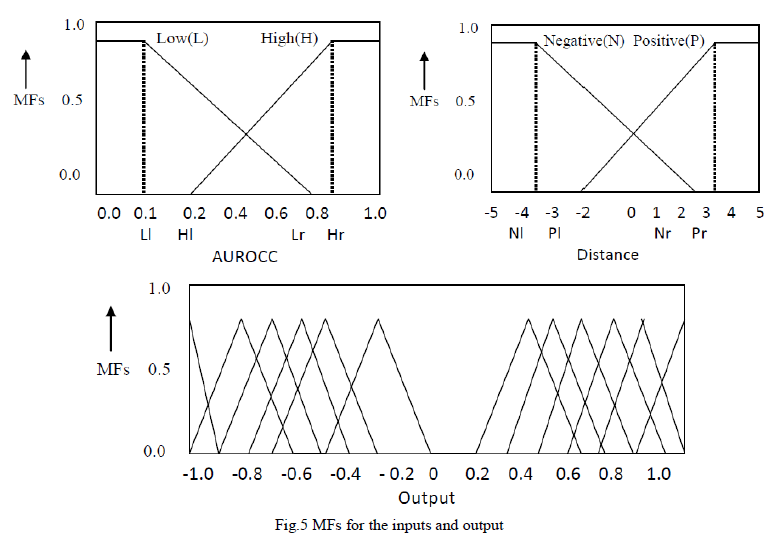 |
| fuzzy sets: negative and positive. The output is composed of 64 fuzzy sets corresponding to the consequences of 64 fuzzy rules. All the MFs are not fixed and each has control parameters to control its position and shape. Each AUROCC MF or distance MF has two control points and each output MF has one control point. We will discuss how to tune the MFs later. |
Fuzzy Rule Base |
| There are 64 rules in total each corresponding to one of 64 combinations of six inputs (2 ^ 6 = 64). The ith (i = 1...64) fuzzy rule is defined as follows: |
| IF aurocc1 is Ai1 and aurocc2 is Ai2 and aurocc3 is Ai3 AND dis1 is Di1 AND dis2 is Di2 AND dis3 is Di3, THEN gi is Oi (i = 1...64). |
| Where auroccj denotes jth AUC input and disj denotes jth distance input (j=1..3). Aij (j=1..3) denotes the AUROCC fuzzy set in {Low, High}, Dij (j=1..3) denotes a distance fuzzy set in {Negative, Positive}, and Oi denotes an output fuzzy set in {O1...O64} for the ith rule. |
Fuzzy System Output and Defuzzification |
| The system output is calculated by aggregating individual rule contributions |
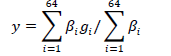 |
| Where gi is the output value of the ith rule and ïÃÂâ i is the firing strength of the ith rule defined by product tnorm: |
| Where μAij (aurocci) and μDij (disj) are the membership grades of input auroccj and disj (j=1…3) in the fuzzy sets Aij and Dij. |
| If the output value is greater than or equal to 0, the data example is defuzzified in the positive class. Otherwise, it is in the negative class. This information may be used to calculate the accuracy of the model. |
TUNING FUZZY SYSTEM USING GA’S |
| To tune fuzzy MFs, there are two techniques in general: Pittsburgh approach and Michigan approach. Pittsburgh approach is to represent an entire fuzzy rule set as a chromosome and maintain a population of candidate rule sets using genetic operations to produce new generations of rule sets. Michigan approach is to represent an individual rule as a chromosome and the whole rule set is represented by the entire population. |
| We use a real-coded GA and apply Pittsburgh approach to tune the input and output MFs. Each chromosome is composed of the 72 genes representing 72 entire membership control parameters: 4 control points for AUROCC, 4 for distance MFs, and the rest 64 for output MFs. The fuzzy MFs are tuned in cross-validation manner. The fitness of the GA is defined to maximize the average AUROCC of each fold of data examples by applying the same MFs defined in a chromosome. |
| The data in Phase I in Fig.4 are classified using SVM Light software. The genetic fuzzy system is constructed and tuned in cross-validation manner as well. Each training dataset in Phase I is further divided into second-level training and testing data. The second-level training data are still trained by SVM Light to obtain the AUROCCs and distances of the second-level testing data (validation data in Fig. 2), which will be used as the inputs of the genetic fuzzy fusion system to tune the optimal fuzzy MFs based on AUROCC measure. After the optimal MFs are adapted, the testing data in the first-level are applied to the tuned optimal fuzzy fusion model to make the final decision. The genetic fuzzy fusion system combining three SVM classifiers has been implemented in C++ language. |
| The proposed SVM fusion model demonstrates stable and robust classification capabilities. It not only performs far better than the average of three individual SVM classifiers in terms of both AUROCC and accuracy, but also outperforms the best of three individual SVMs in terms of accuracy and achieves as least as much performance as the best in terms of AUROCC. The genetic fuzzy SVM fusion model based on AUROCC produces a combined classifier with the best AUROCC naturally because of the properties of AUROCC. |
EXPERIMENTAL RESULT AND ANALYSIS |
Historical data |
| To evaluate the proposed method, we use the dataset acquired by NTPC-Korba India. It includes the records for 345kV and 154kV transformers operated in two different areas during 1992-1997. These patterns are acquired from transformers in two regions in Korba. There are 963 DGA patterns acquired from 177 transformers in 64 substations located in the same region and 471 patterns acquired from 98 transformers in 38 substations in another region. Each pattern consists of H2, O2, N2, CO2, C2H4, C2H6, C2H2, CH4, CO, and T.C.G. Among these gases, we chose 963 patterns for the training purpose, while the rest of the data were used for testing. |
| Fig.6 shows Output of SVM classifiers fusion model i.e. Amount of specific Gas. Here, we consider the 7 specific gases such as H2, CO, C2H2, CH4, C2H6, C2H4, and CO2, which are described from number 1 to 7 in this Fig.6. From this Fig.6, we see that each condition has the characteristics according to the amount of specific gas. For example, care condition for insulator degradation has more CO gas than the other conditions. Otherwise, the amount of CO gas is less than 0.7 under normal conditions. Here the number of inputs equals the kinds of specific gases considered in this architecture. Also, the number of outputs equals the kinds of care conditions plus the normal condition. Care conditions include the six types such as insulator degradation, CO2 excess, arc discharge, low overheat and high overheat. Therefore the numbers of input and output are 7 and 6, respectively |
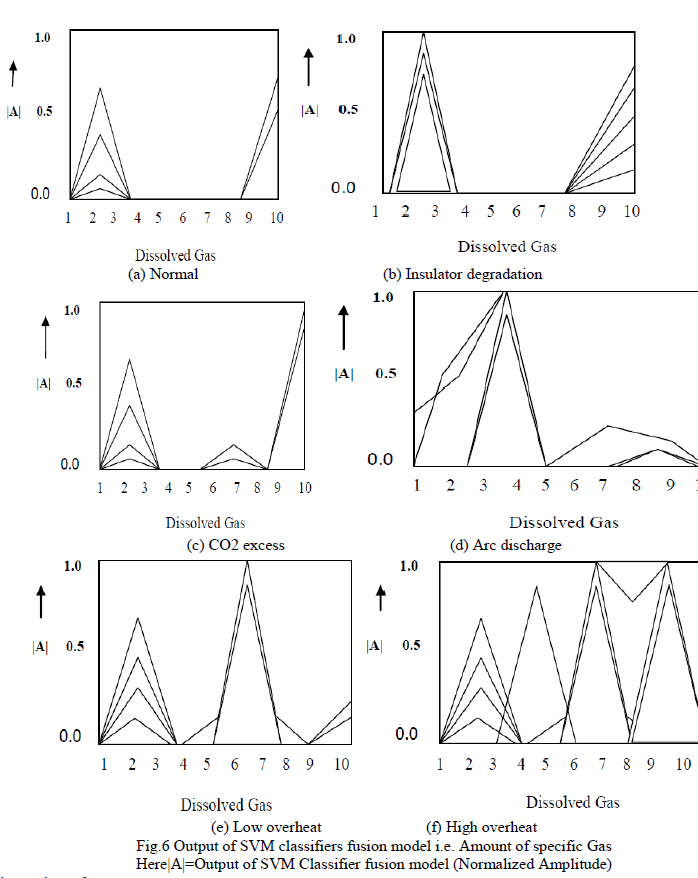 |
Diagnosis performance |
| Fig.7 presents the output value for the normal condition among the output units in SVM classifiers fusion model according to the normal and care dataset determined by experts for normal mode. The values of most of the normal data are higher than 0.4. Otherwise, the output unit corresponded for normal state has the value less than 0.25 for care data. |
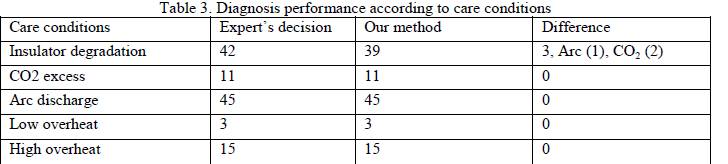
| Table 2 shows the diagnosis results with respect to normal and care conditions. From this table, the result by our method is equal to the expert’s decision. However, the result for normal data is slightly different from the decisions made by the experts. The reason for this could be well explained by Fig.7. According to the decision rule performed by NTPC-Korba, if the amount of gas for CO (described as number 2 in the fig.7) is less than 300, the transformer is determined as normal. Also, if the amount of gas for CO2 (described as number 10 in the fig.7) is less than 4000, the transformer is determined as normal. More specifically, the values of gases are 287 and 3460 for CO and CO2, respectively. By considering these relations, our method concludes that this transformer is in care condition. Table 2 indicates the diagnosis performance according to care conditions. As seen in Table 3, the diagnosis performance by our method shows the same decision criteria comparing with the determination by expert’s except for insulation degradation. |
 |
| Analysis of aging degree for normal transformer |
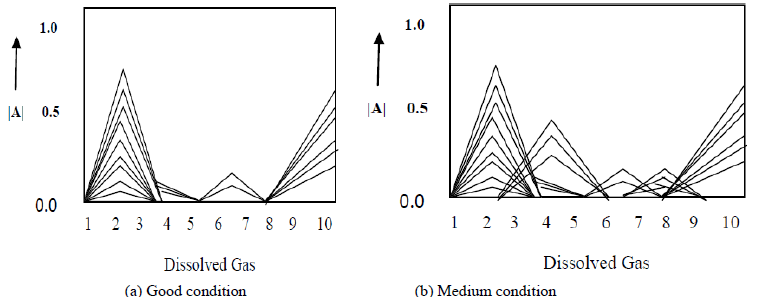
| Specific gas is generated and accumulated in the oil as time goes on in spite of the normal condition. Therefore, potential possibility and degree of aging could be different even with transformers that are in normal condition. In fact, the amount of these gases indicates a potential of approaching to a care or a faulted condition as well as being in those conditions. For analyzing the aging degree for normal state, we classify the normal condition as three types such as “Good”, “Medium”, and “Low”. This criterion is performed by considering output value of a normal unit in the RBF neural network. More specifically, when the output value is larger than 0.88, our method determines that the transformer is definitely in “Good” condition. Table 4 shows the diagnosis results according to healthy conditions. By applying this technique, we analyze our data according to healthy conditions. As seen in Fig.8, we see that most transformers are in “Good” condition. |
 |
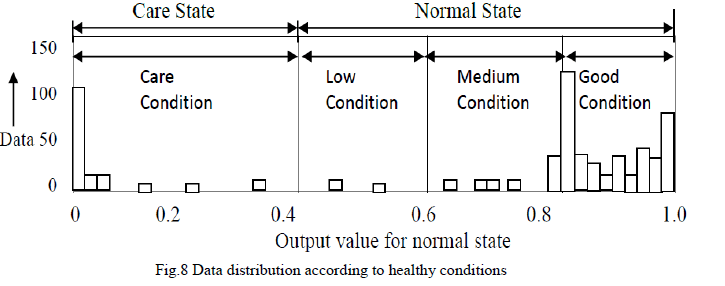
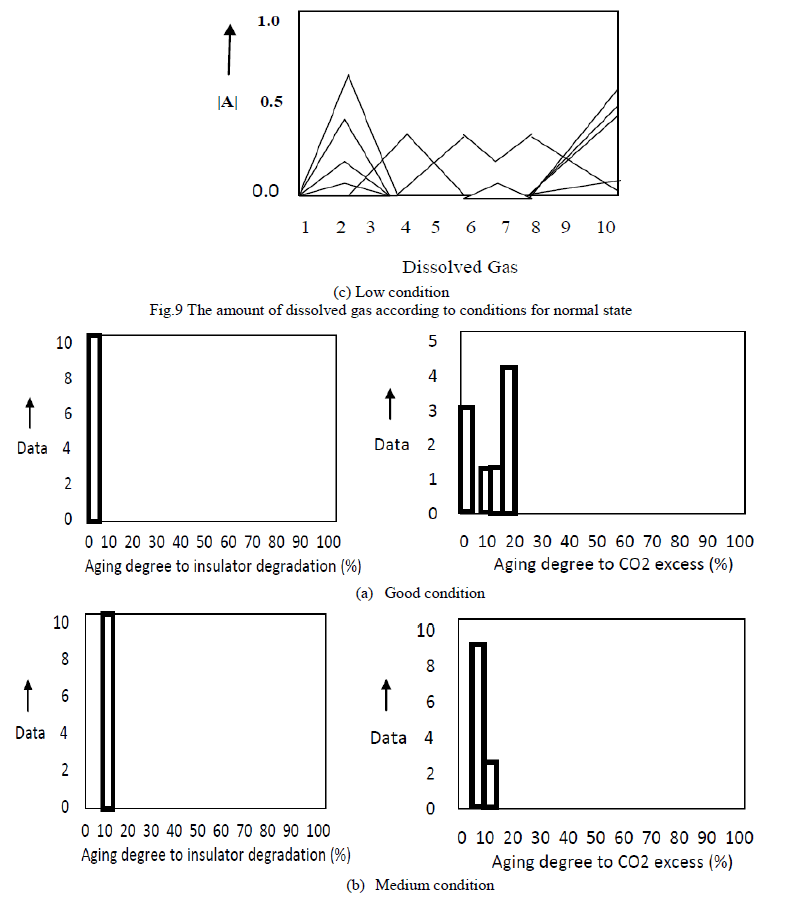
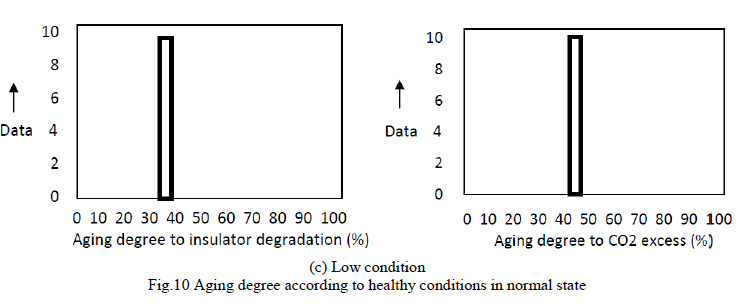
| Fig.9 shows the amount of dissolved gas according to healthy conditions for normal transformers. From Fig.9, the amount of specific gas is increasing according to aging degree such as from “Good” condition to “Low” condition. Fig.10 indicates the aging degree according to healthy conditions in normal state. This figure displays the aging degree with respect to insulator degradation and CO2 excess. |
| From these results, the aging degree increases as the condition changes from “Good” to “Low” condition. Especially, aging degree is close to 45% in case of transformers in “Low” condition. From these experimental results, we are convinced that our method makes it possible to estimate the aging degree for normal transformers as well as the causes of transformers in care conditions. |
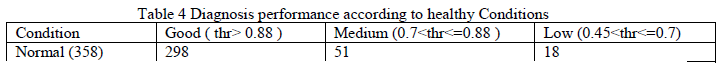 |
 |
 |
 |
 |
CONCLUSION |
| In this paper, we proposed a method of power transformer diagnosis using AUROCC-based Genetic Fuzzy SVM fusion model. Here, we propose a genetic fuzzy SVM classifier fusion model to combine multiple SVM classifiers. Individual SVMs are combined in a genetic fuzzy system and GAs is applied to tune the fuzzy MFs based on AUROCC measure. The experimental results show that the proposed genetic fuzzy system is more stable and more robust than individual SVMs. Moreover, the combined SVM classifier from the genetic fuzzy fusion model accomplishes more accurate ranking of data examples which provides valuable interpretation of the real-world data and may help dissolve gas analysis (DGA). From various experimental results, we conclude that the proposed method is efficient in estimating the aging degree for normal transformers as well as the cause of transformers in care conditions. The objective of this paper is to develop an AUROCC-based genetic fuzzy SVM fusion model and then this model is used for Dissolved Gas analysis (DGA) in power transformer. The results compare diagnostic performance according to normal, care and healthy conditions with respect to our method and expert’s decision are discussed. Also aging degree of power transformer for insulation degradation and CO2 excess for good, medium and low conditions are demonstrated |
References |
|