Downlink Resource Allocation for Next Generation Wireless Network Using Turbo Codes over Non-Linear Channel

Abstract

In this project, a downlink resource allocation scheme for OFDMA-based next generation wireless network targets high data rate and efficient resource usage the scheme consist of radio resource and power allocation which are implemented separately. Low complexity heuristic algorithm are first proposed to achieved the radio resource allocation, where graph base framework and fine physical resource block assignment are performed to mitigate major ICI and hence improve the network performance. A novel distributed power allocation is then performed to optimize the performance of cell edge users under desirable conditions. The power optimization is formulated as an iterative barrier constrained water filling problem and solved by Lagrange method. Joint ML MMSE is used to develop simple receiver structure that gives joint ML estimates of multipath channel and the transmitted data sequence. Simulation results indicate that our proposed scheme can improve performance of cell edge users in multicell network

INTRODUCTION

Radio spectrum is becoming a scarce resource in wireless communications, the orthogonal frequency division multiple access (OFDMA) has been proposed as a state-of-the-art air interface technology to enable high spectrum efficiency and effectively combat frequencyselective fading. Due to its promising features, OFDMA is adopted in many emerging cellular systems such as the Long Term Evolution (LTE and IEEE 802.16m) for achieving those ambitious objectives of next generation networks. In order to realize the flexibility on access of radio resources, OFDMA poses a new challenge for radio resource management (RRM). A good RRM scheme, including subcarrier allocation, scheduling and power control, is crucial to guarantee high system performance for OFDMA-based networks. 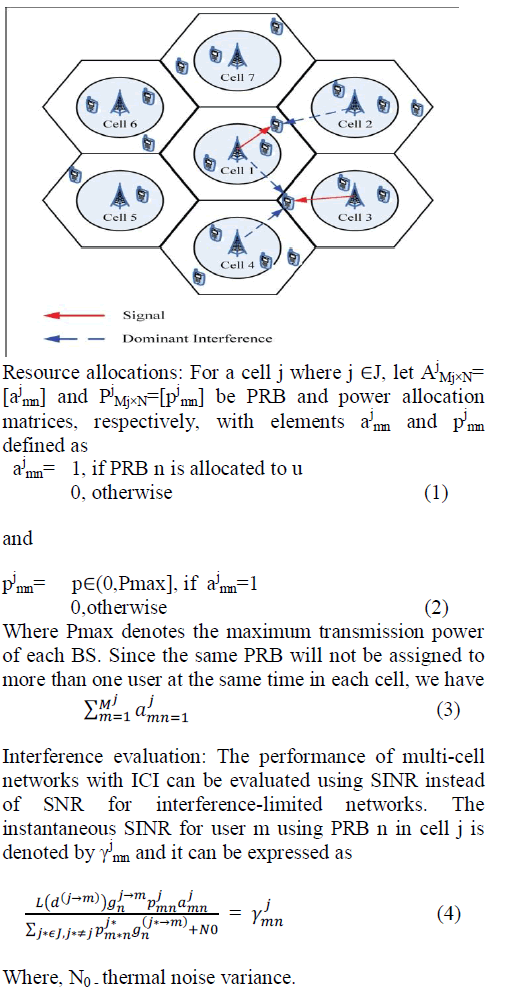In future wireless networks, however, denser cellular deployment with a lower frequency reuse factor is demanded. This has moved the trend to the development of RRM for multicell systems. In the multi-cell context, inter-cell interference (ICI) has become a major issue of concern since the frequency reuse-1 is agreed as the preferred frequency planning deployment for modern OFDMA-based cellular networks. Due to the same spectral usage in adjacent cells, ICI can result in severe performance degradation to users of reuse-1 OFDMA networks, particularly those at the cell edge. Thus, developing RRM schemes with an emphasis on ICI reduction in the multicell scenario is of significant interest to recent research work. The ICI-aware RRM in multi-cell OFDMA networks, in general, can be formulated as a global performance optimization problem by considering the signal-to-interference-and noise ratio (SINR) instead of the signal-to-noise ratio (SNR). Unfortunately, finding the optimal solution to such a global optimization problem is extremely hard and normally not applicable in practice. This is because the problem has been known as a mixed integer programming (MIP) and proven to be NP-hard, which is computationally prohibitive to tackle. The first category aims at developing intelligent subcarrier (or sub channel) allocation schemes to effectively mitigate ICI and improve the system performance. This is known as ICI coordination (ICIC). As the subcarrier Allocation can be formulated as a binary integer programming (BIP) which is an NP-hard problem as well, heuristic algorithms were proposed to simplify the process of subcarrier allocations. The second category, on the contrary, has mainly concentrated on using power allocation to maximize network throughput. Unlike the subcarrier allocation case, finding the optimal solution for power allocation might be feasible if the formulated problem can be proven to belong to the class of convex optimization problems. A Lagrange dual method and geometric programming have been proposed to tackle such optimization problems. However, the perfect convex structure on power allocation holds only for the single-cell scenario in the absence of ICI. The sum rate or system throughput of multiple cells is not convex (or concave) in terms of the power allocated to each user. This lack of a convex structure makes it impossible to obtain the optimal solution in multi-cell scenarios. In a boundary of the feasible region for such non-convex problems has been investigated and accordingly optimal power allocation schemes were proposed. Yet due to high complexity, those schemes only work well in a simple two-cell scenario and have not been tested under the environment with high network densities.

PROBLEM FORMULATION

Consider a downlink cellular network consisting of a set of BSs denoted by J= {1,...,J},where J is the total number of cells in the network. The total number of users in cell j is denoted by Mj, while the number of available PRBs that can be scheduled for downlink data transmission in each TTI is denoted by N. Note that each BS is allowed to use all NPRBs as the frequency reuse-1 deployment is applied in the network.

Optimization Problem: Here our optimization goal is to maximize the overall throughput of cell-edge users while maintaining the required throughput for cell-centre users. As a result, a balanced performance improvement between cell edge and cell-centre users is expected to be achieved in the multi-cell systems. The reason behind this is that cell-centre users usually do not suffer from heavy ICI and relatively high performance is easy to be obtained for these users even in a network without optimization, whereas cell-edge users’ performance is much more vulnerable to ICI and their performance improvement has to strongly rely on optimization schemes. Thus, in this work the resource allocation are formulated as the following maximization problem with constraints.

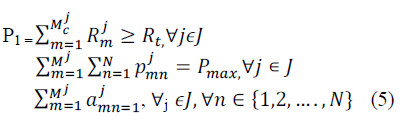Where Mj E and Mj C denote the total number of cell-edge Users and cell-centre users in the given cell j, respectively, i.e., Mj E+Mj C =Mj, and Rt is a throughput threshold Defined to satisfy cell-centre users of each cell with preferred Performance achievement. Clearly, the solution to this problem is not to address the general global optimization but to achieve a better performance balance, where different types of users in the network can equally obtain desirable data rates regardless of their geographical locations.

PROPOSED RADIO RESOURCE ALLOCATION

Phase I: ICIC

In the multi-cell context, the resource allocations have to start with the global ICIC schemes as effective ICI mitigation cannot be achieved only by power control especially for those cell-edge users who are close to each other in the network. Thus, the first phase of our proposed radio resource allocation is to develop an ICIC scheme using a simple but effective graph-based framework. Our objective is to construct a graph that reflects major interference occurring in the real time

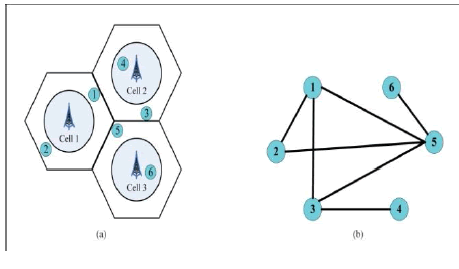Fig.3 An example of the graph-based framework. (a) 3- cell scenario. (b) Interference graph construction. network environment. According to the graph theory , the corresponding interference graph is denoted by G=(V,E), where V is a set of nodes each representing a user in the network, and E is a set of edges connecting users that can cause heavy mutual interference when they are allocated the same PRB. In order to reduce complexity, the interference intensity for edge connections is determined solely by the geographical location and proximity of users in the network. i.e., celledge users suffer from severe interference due to the shorter distances to the adjacent BSs. The information for precise SINR measurements is not required at this stage. For building the edge connection per pair, we define that the edge between user a and b is connected when E(a, b)= 1,otherwise,E(a, b)=0, and note that E(a, b)=E(b, a).

The basic rules of the interference graph construction are as follows.

 Users within the same cell are mutually connected.

 For any cell-edge user, the connection is only pair wise established with other cell-edge users of its dominant interfering cells.

Let Dm denote the set containing indices of dominant interfering cells to cell-edge user m. Thus, an illustrative example is given by Fig. 3. Fig. 3(a) presents a simple 3- cell network case, where user 1, 2, 3 and 5 are cell-edge users of each cell and D1 ={1},D2 =∅,D3 ={3},D5 ={1,2}, respectively. Then the corresponding interference graph is constructed in Fig. 3(b).

Phase II: Fine PRB Assignment

The first phase framework offers the network with a strategic planning for ICIC but the actual PRB allocation has not been done yet. In the second phase, therefore, we will decide how to practically make the PRB assignment in the network given the interference graph. This work is also known as the colour mapping problem in general graph theory by marking those directly connected nodes with different colours. To reduce complexity, a heuristic algorithm is proposed here to perform a fine PRB allocation by taking account of the instantaneous channel quality. Since major ICI is well looked after by the first phase, in the second phase we consider only SNR for simplicity by removing the interdependency issue of SINR. SNR for user m on PRB n is calculated by,

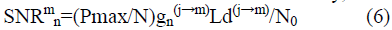where j is the serving cell of user m. Let Rm be the set of users who are allowed to have the same PRB, or in another word, the same colour with user min the network. Note that finding the necessary Rm is also included in this algorithm. The PRB allocation decision made to a user is determined not only by the instantaneously achieved SNR but also by a weighting factor denoted by wm. Based on the weighted SNR, the PRB allocation that effectively achieves an overall performance improvement with good fairness among those two types of users in the network. On the other hand, the proportional fairness is also considered by taking account of the number of PRBs already occupied and there by prevents the PRB resource allocation schemes. On the other hand, cell-centre users are allowed to share PRBs with all users in the network (except their serving cells) and thereby may interfere with either celledge or cell-centre users of the adjacent cells depending on the PRB allocation.

OPTIMIZATION FOR CELL EDGE USERS

Power allocation for cell edge users

Given the fixed PRB allocation and power allocation of Cell centre users, the original optimization problem P1 becomes a convex function of power of cell-edge users and can be decomposed into J parallel sub-problems, where the optimal power allocation to cell-edge users is solved locally by each BS of the network. Note that such sub-problems are defined as a series of P2, where only mutual interference between cell-edge and cell-centre users is taken into account. Let pj(e) n denote the power allocated to PRB n used by a cell-edge user in cell j. Therefore, the objective of P2 for cell j is expressed

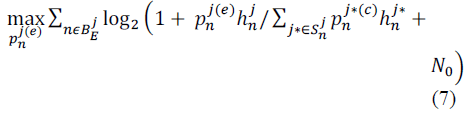Where hj n(hj∗n) denotes the combined channel impact on PRB n in cellj(j∗) including the channel gain and path loss fading components presented in (3), i.e.,hj n=g(j→m) n Ld(j→m), and Sn is a set of neighbouring cells in the network (i.e.,j∗=j,∀j∗∈J) , in which PRB n is used by a cell-centre user at the moment. The idea of P2 is to use power allocation to maximize performance of cell-edge users under the constraint that performance of cell-centre users is not largely sacrificed. Power allocation to celledge users has to be conditionally optimized in order not to generate unacceptable interference to cell-centre users in the network. In addition, here we assume that the required information about the power allocation of cellcentre users in adjacent cells is known by each BS, which in fact are achievable in future wireless networks where specific links, such as the X2 interface in LTE are built to connect BSs for necessary information exchange among them.

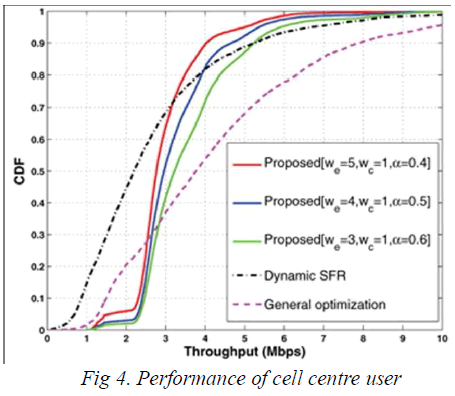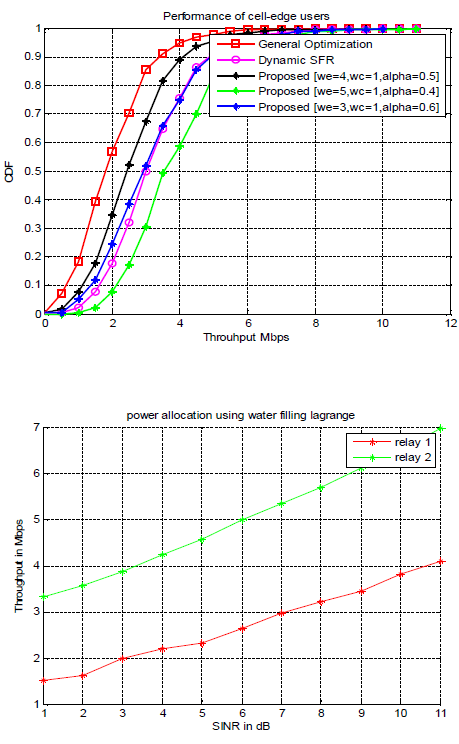
SIMULATION RESULTS

The proposed scheme can consistently balance the performances of cell edge users and cell centre users

CONCLUSION AND FUTURE WORK

As a result, proposed resource allocation scheme improves the performance of cell-edge users which allows for future wireless networks to deliver consistent high-performance to any user form anywhere. For future enhancement, simulation of handoff technique is said to be done in LTE network and MIMO - OFDM is compared in terms of BER.

References

D. Astely, E. Dahlman, A. Furuskar, Y. Jading, M. Lindstrom, andS. Parkvall, “LTE: the evolution of mobile broadband – [LTE part II:3GPP release 8],”IEEE Commun. Mag., vol. 47, no. 4, pp. 44–51,2009. K. Etemad, “Overview of mobile WiMAX technology andevolution,”IEEECommun. Mag., vol. 46, no. 10, pp. 31–40, 2008. Z. Shen, J. G. Andrews, and B. L. Evans, “Adaptive resourceallocation in multiuser OFDM systems with proportional rateconstraints,” IEEE Trans. Wireless Commun., vol. 4, no. 6, pp. 2726–2737, 2005. Y. Lin, T. Chiu, and Y. Su, “Optimal and near-optimal resourceallocation algorithms for OFDMA networks,” IEEE Trans. WirelessCommun.,vol. 8, no. 8, pp. 4066–4077, 2009. J. Jang and K. Lee, “Transmit power adaptation for multiuserOFDM systems,” IEEE J. Sel. Areas Commun., vol. 21, no. 2, pp. 171–178, 2003.