ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Atreya, Prashant1, Islam, Najrul2 Alam, Mehtab3, Hassan, Syed Danish4
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
All the researchers in past have carried out dynamic response analysis of the structure under Wave, Earthquake or Wind loads or a combination of these loads and studied its behavior. Very few investigations have been reported which effectively incorporate hydrodynamic drag nonlinearity and study its effect on the stability of the systems. As oceanic waves are better modeled as stochastic process, there is a need to investigate the stochastic stability of flexible offshore structures as well. Present study have been carried out to determine seismic response of single hinged Articulated Tower under Wave and Earthquake loads followed by its dynamic Stability analysis. Dynamic stability analysis of compliant offshore structures constitute an interesting area of research because of their inherent non-linearities. The study has explored dynamic instabilities existing during the different phases of wave / earthquake loading on SHAT. A simple method of two-dimensional phase plots and bifurcation assessment has been used to identify phases of dynamic instability existing within the responses of SHAT under various conditions of loading.
Keywords |
| Single Hinged Articulated Tower, Earthquake, Time History, Phase Plot |
INTRODUCTION |
| Complex non-linear and chaotic responses are observed in various types of compliant offshore structures. These structures have large displacements with inherent non-linearities, so prediction of behavior of these structures in oceanic environment is difficult and is met with many challenges. These systems are characterized by strong geometric non-linearity, non-linear excitation forces in form of waves and earthquake and non-linear restoring forces. The non-linear restoring forces arising due to fluid structure interaction finally leads to the possibility of dynamic instability of the systems. On account of these non-linearities, numerical investigations of compliant offshore structures have revealed complex behavior involving subharmonic, super-harmonic and aperiodic solutions[1,2 & 3]. |
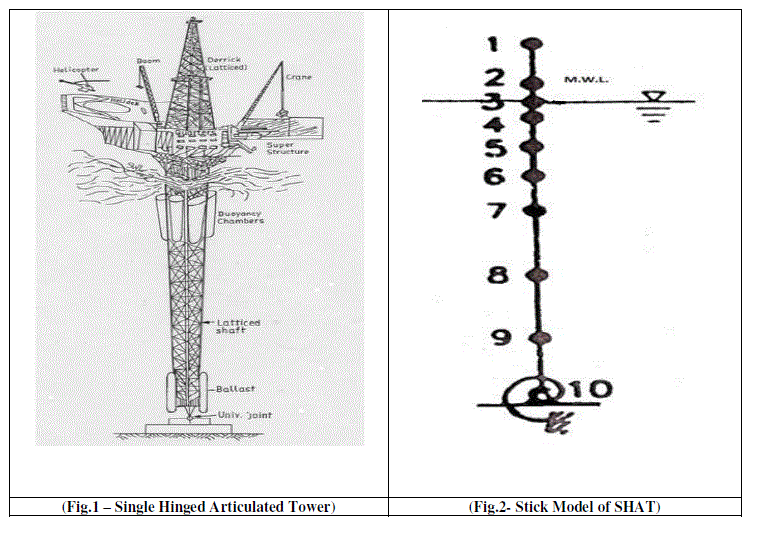
| SHAT platform is one of the compliant structures(Fig.1) which is economically attractive especially as loading and mooring terminal in deep waters. These platforms are comparatively light compared to the conventional fixed platforms. The tower itself is a linear structure, flexibly connected to the sea bed through a cardon / universal joint and held vertically by the buoyancy force acting on it. The part of the tower emerging from the water supports the super structure designed to suit the particular application e.g. a tanker to be loaded, flaring of waste gases, etc. As the connection to the sea bed is through the articulation, the structure is free to oscillate in any direction and does not transfer any bending moment to the base. As the articulated tower is compliant in nature, it moves with the waves and thus the wave force and bending moment along the tower will be less compared to a fixed structure. Efforts have been made to use simplified realistic mathematical models to gain important insight into the response behavior of these structures and to explore the possibility of their dynamic instability and chaotic motion. |
II. STRUCTURE IDEALIZATION AND SYSTEM MODEL |
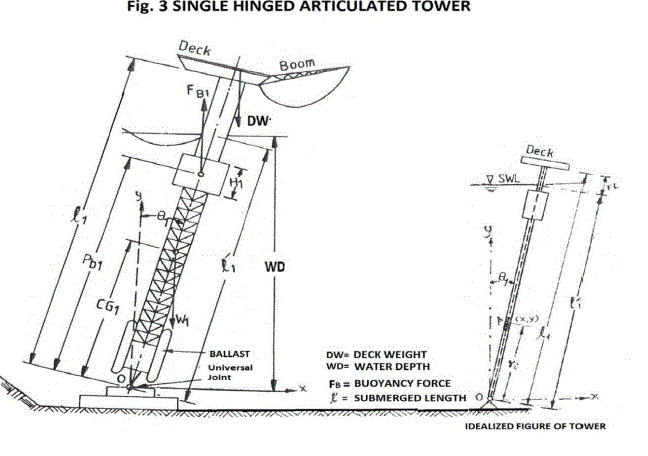
| SHAT has been modeled as a stick. The universal joint at base has been modeled as mass-less rotational spring of zero stiffness. The main piles are assumed to cluster near the centre of the tower cross-section, hence soil reaction at the sea-bed is modelled as rotational spring of fairly small stiffness, considered as zero (Fig. 2). The problem has been solved using Finite element method. The submerged elements of the tower have been subjected to time dependent hydro-dynamic loading and elements of the tower above still water level have been exposed to wind forces. Due to non-linear forces acting on the tower, the number of submerged elements also varies with respect to time. Drag force has been assumed to be proportional to the relative water particle velocity w.r.t. the structure, oscillating under wave and ground motion. The structural damping of the system has been specified as a fraction of the critical damping corresponding to the un-deflected configuration of the tower. |
 |
III. SOLUTION APPROACH TO DYNAMIC STABILITY ANALYSIS OF SEISMIC RESPONSE OF SHAT |
| In Articulated Towers, due to large rotations, displacements and relative structural and water particle velocities, equation of motions become highly non-linear. Since at each time step, the instantaneous submergence, inclination and geometry of the tower changes appreciably, the buoyancy, added mass, stiffness, hydrodynamic forces and damping also changes. Due to combined effect of instantaneous tower’s orientation, current and variable free water surface profile, this variation is much pronounced. Lagrange’s method has the capability of relating the Kinetic, Potential energies and work of the conservative and non-conservative forces in terms of generalized rotational degrees of freedom. So, Lagrange’s approach has been used to arrive at non-linear dynamic formulation of articulated tower. |
| Wave forces on the submerged part of the tower have been estimated by the modified Morison’s equations, which duly takes into account the relative motion of the structure and water. Seismic inputs have been applied using El-Centro / Northridge spectra. The water particle velocities and accelerations has been stipulated by Airy’s Linear wave theory. To incorporate the effect of variable submergence, Chakrabarti’s approach [4 & 5] has been adopted. The transformation matrix has been used to compute the normal and tangential component of the hydrodynamic forces on each element of the tower corresponding to instantaneous deformed configuration of the tower. The updated mass-moment of inertia of the tower has been incorporated in the consistent mass and damping matrices. Newmark’s Beta integration scheme has been deployed to solve the equation of motion taking into account all non-linearities involved in the system. The responses obtained were subjected to dynamic stability assessments. |
| Let us consider SHAT model in Fig.3. Flow chart for solution is given at Chart.-1. |
 |
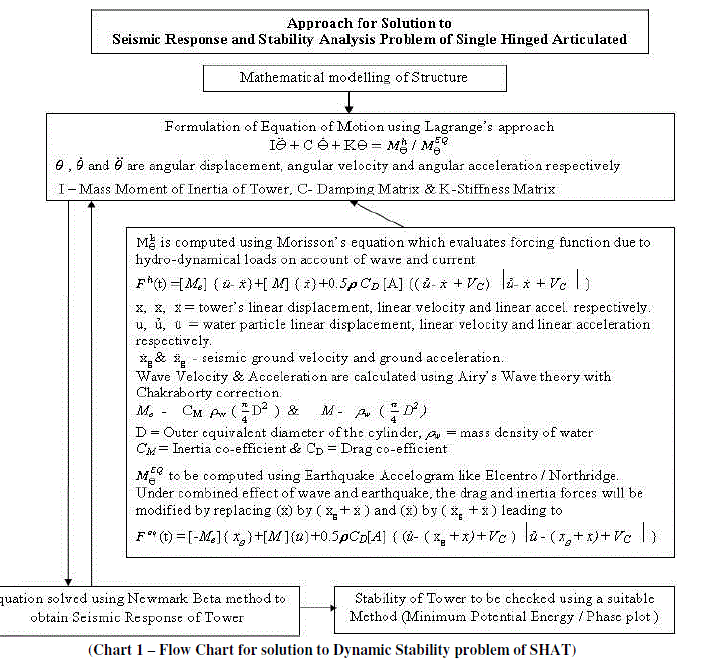 |
| The equations mentioned in the chart, after integration, have been used to determine the instantaneous hydrodynamic loading along the submerged height of the shaft. Moments about the axis of rotation, due to these forces are determined by multiplying the differential force equation by the appropriate moment arms and then integrating over the length of the cylindrical shaft to obtain the total moment. As the total height of the shaft shall be divided into a finite number of elements for determination of the wave forces and moments. The total force is obtained by the summation of all elemental values. The above Equations were solved to obtain the transient responses at Heel and Deck level in form of angular deflection, angular velocity, angular acceleration etc. These were further solved to obtain the Shear Force, Bending Moment, Axial Force, Base Shear Force etc. along the axis of SHAT during various time intervals thereby providing total transient behavior of the tower. |
IV. DYNAMIC STABILITY SOLUTION USING CONCEPT OF PHASE PLOT & BIFURCATION |
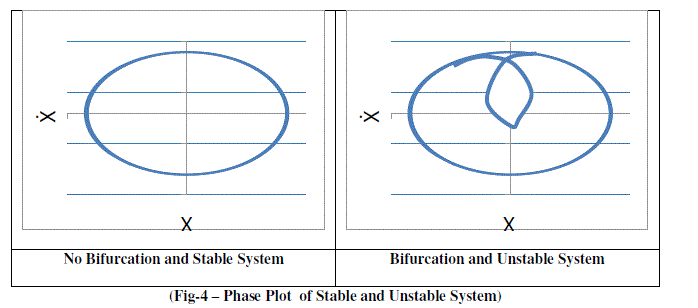
| A phase portrait is a collection of trajectories that represent the solution of these equations in the phase space. To obtain phase plots, velocities are plotted on abscissa and displacement / rotation are plotted on x-axis. In general, a phase portrait contains information about both the transient and the asymptotic behaviors of the solutions of a system. The phase plots are extensively used to identify transitions of solutions from stable to unstable zone[8]. In Phase Plots, instability phenomenon is shown in form of symmetry breaking bifurcations caused by nT sub-harmonic / super-harmonic oscillations and aperiodic responses. The bifurcation concept is a mathematical study of changes in qualitative or topological behavior of structure[6]. Without occurrence of bifurcation, the system seems to be quiet stable. In reality bifurcations may occur in both continuous and discrete systems. In a dynamical system, a bifurcation occurs when a small smooth change made to the bifurcation parameter causes a sudden qualitative or topological alteration in structural behavior. When the symmetry of a Phase Plot is disturbed, bifurcation is termed as symmetry breaking bifurcation. Sub-harmonic oscillations occur when the time period of subsequent cycle lessens by 1/n times than the previous time period. When the time period of subsequent cycle increases n times of previous time period, the oscillation is super-harmonic. |
 |
V. RESULTS AND DISCUSSION |
| A Single Hinged Articulated Tower with following structural parameters was subjected to longer duration (2000 sec.) of moderate regular sea wave load having height as 2.15m and time period as 4.69 sec[7]. Wave load was applied at 0 sec. and after the excitation impact due to wave load got stabilized due to hydrodynamic damping, Northridge Earthquake load was applied at 498.4 sec. To assess the dynamic behavior of Tower at various stages, analysis was done for a longer duration of 2000 sec. of wave load. |
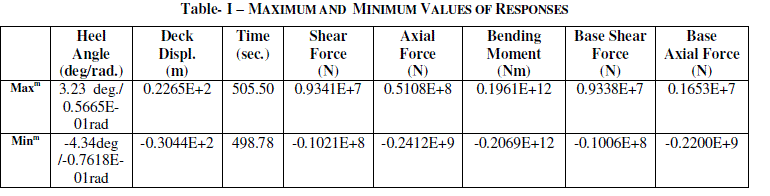 |
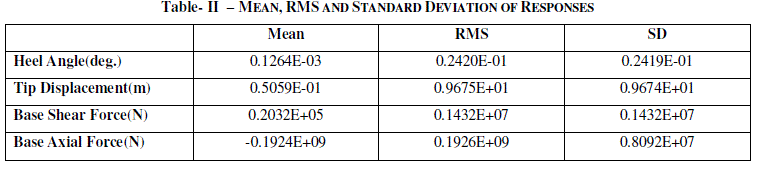
| The Responses obtained in form of various parameters are given in Table I, II & III. The Time period of SHAT was obtained as 29.4 sec. |
 |
 |
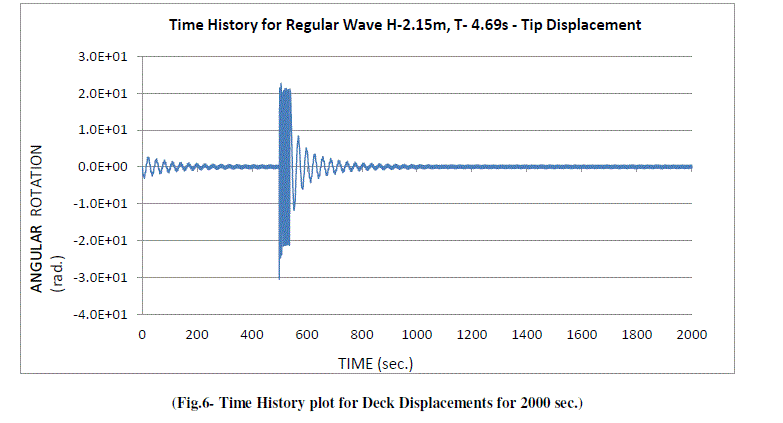 |
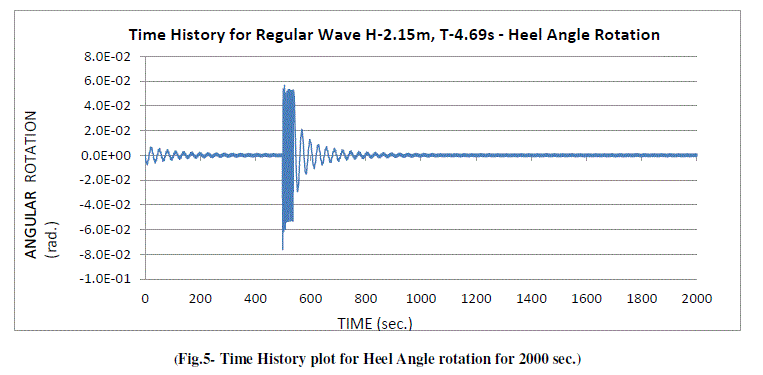
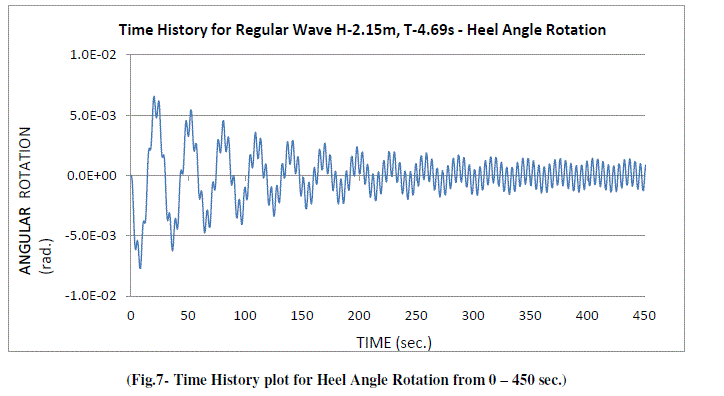
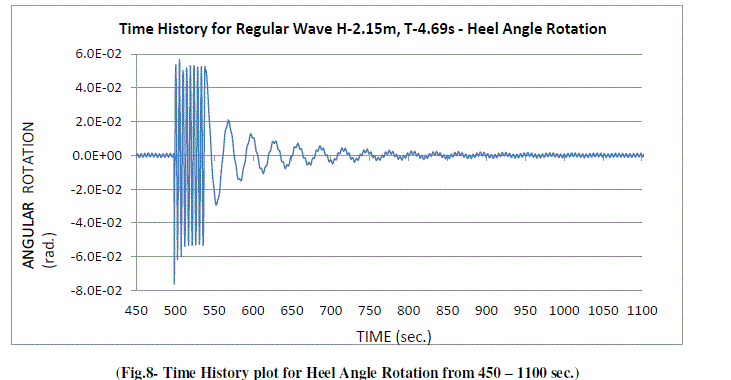
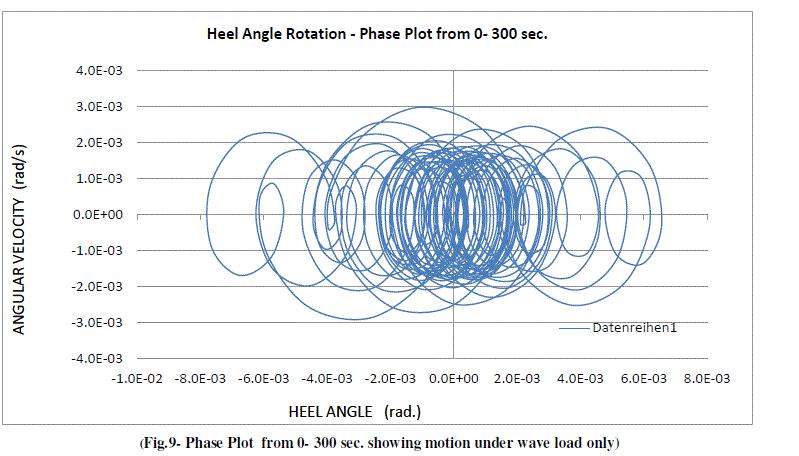
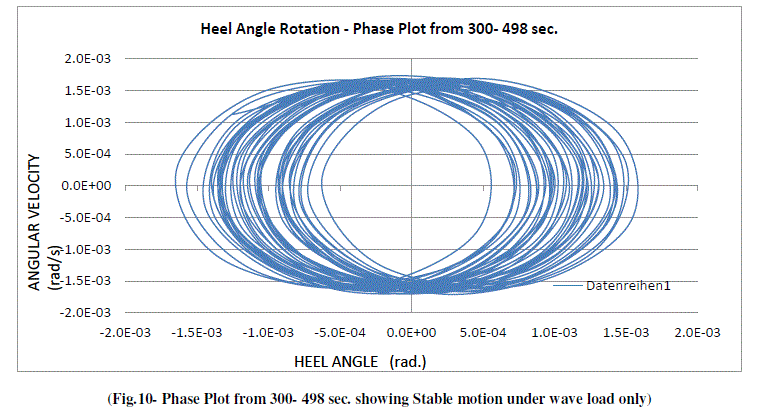
| Fig.5 and Fig.6 show the Time History plots for complete duration of 2000 sec. of loading. Fig.7 and Fig.8 give the enlarged view from 0 – 450 sec. and 450 – 1100 sec. As the motion got stabilized after 300 sec. of wave load, the shape of the wave became uniform. After impact of Earthquake load at 498.4 sec., system took another approx. 300 sec. to settle down, but not fully. The dynamic stability phenomenon during various phases of loading is more visible in the following Phase Plots for Heel Angle rotation which are given from Fig.9 to Fig.14. |
 |
| The Phase Plot from 0 - 300 sec. shows the motion as aperiodic, non-harmonic and asymmetric having closed path. This phase shows dynamic instability. The hydrodynamic damping slowly brings the system back to normalcy and as shown in Fig.9, the system becomes dynamically stable from period 300 – 498 sec. During this duration, the motion became periodic, harmonic and symmetric with no bifurcation. With the application of Earthquake load at 498.4 sec, due to excitation impact, bifurcations are visible in the phase plot (Fig.10). The responses are non-harmonic, asymmetric and aperiodic in nature. The sub-harmonic / super-harmonic characteristics induced by non-linearities of the of system are visible in the motion. Therefore, during this phase from 498 – 538 sec., the motion is dynamically unstable in terms of bifurcation of responses as well as nT harmonics. Maximum heel angle displacement during earthquake has been 4.34 degrees, which fall very much outside the serviceability limits for providing drilling and mooring operations by the Tower. But throughout the duration of loading, there have been net positive stabilizing forces acting on the Tower, which have the tendency to bring the Tower back to its mean position. |
 |
 |
 |
VI. CONCLUSIVE REMARKS ON STABILITY ANALYSIS OF SHAT |
| In addition to above load case, the SHAT model was also subjected to a vide variety of regular waves with different Earthquake loading combinations. Few conclusions drawn are given below: |
| 1. It has been seen that subsequent to application of wave load at 0 sec., due to damping effects, the impact of regular wave excitations gradually die out over a period of approx. 8-10 times the time period of the structure. |
| 2. In all the regular wave cases evaluated under the study, it has been seen that dynamic instability is visible during the initial period pertaining to onset of waves or period pertaining to Earthquake loading. During these periods / shorter duration loadings, system is non-harmonic, asymmetric and aperiodic. Sub-harmonics / super-harmonic are existent in system and bifurcations are easily visible in the phase plots confirming the dynamic instability. |
| 3. With the passage of time, the hydrodynamic dampening effects reduce excitation responses. During larger duration loadings, the motion becomes harmonic, periodic and symmetric. No bifurcations are visible on the phase plots and the structure show dynamic stability. The larger size waves dampen out excitations much early as compared to smaller size waves and system becomes dynamically stable at an early duration which gets clearly visible in the Phase plots. |
| 4. The net positive stabilizing forces acting in the system bring the SHAT back to its mean position, thereby assuring stability in all respects. |
References |
|