ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Dr. Basharat Salim Department of Mechanical Engineering College of Engineering King Saud University Riyadh |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Diffusers are used in many fluid flow systems where a need exists for the flow deceleration or pressure enhancement. A wide angle diffuser has larger diffusion angle and area ratio than the common diffuser. Its main use is to restrict length of the diffusing passage for nearly equivalent pressure recovery enhancement. When the flow enters the diffuser inlet it faces an adverse pressure gradient that results in flow separation which causes degradation in the performance of a diffuser by decreasing the pressure rise capability and increasing the total pressure loss. Its performance depends on a complicated interaction between its flow and performance parameters. The present investigations aim at experimentally investigating the flow behavior within a wide angle diffuser to evaluate its performance. The effect of diffuser angle and area ratio of the diffuser has been investigated by testing two types of diffusers at five Reynolds numbers. Four diffusers of diffuser angle 50, 70,100 and120 were used to find the effect of diffuser angle, where as another four diffusers with area ratio 1.56, 1.76, 1.97and 2.24 were used to determine effect of area enlargement for a diffuser angle of 70.To achieve this goal an experimental facility was fabricated around a centrifugal fan which fed air diffuser through a settling chamber and a straight duct. The variations have been shown as velocity ratio with the references of the mean velocity at the inlet of the diffuser. The Reynolds numbers at which investigations were carried out were calculated using free upstream velocity which was measured upstream of the diffuser inlet so as to avoid the influence of the diffuser on velocity profile. The results depict that both the pressure recovery and diffuser effectiveness is better in the diffuser with 70 diffuser angle. The better performance is attributed to the lesser values of the inlet blockage and percentage RMS index for this diffuser. The change in the area ratio of the diffuser with diffuser angle of 70 showed that the change in the area ratio of the diffuser affects the performance parameters of the diffuser and the internal aerodynamics of the diffusers. The diffuser with aspect ratio of 1.76 developed higher pressure rise coefficient and diffuser effectiveness
Keywords |
| Wide angle, Diffuser, Rectangular, Diffusion angle, RMS index, Pressure recovery. |
INTRODUCTION |
| Diffuser forms an important part of most fluid flow systems wher e kinetic energy of flow needs to be converted into pressure energy by decelerating the flow in the direction of fluid motion with a simultaneous increase in static pressure. Wide angle diffuser is commonly used in many industries as it allow a short and rapid transition from inlet ducting to a collector of larger cross section. It is a short diffuser, with a large area ratio and a large equivalent cone angle. It provides excellent performance in low flow situations and their dump-resistant performance makes them well suited for cold air applications. Japikse [1] has opined that the diffuser effectiveness serves as the parameter for showing the performance of a conical diffuser up to an area ratio of 20, beyond this area ratio the diffuser effectiveness and the pressure recovery has to be considered separately. Gibson [2] was probably the first to make systematic study of conical, square and two dimensional diffusers and found optimum divergence angle for conical diffusers to be 60 for square diffusers and 110 for rectangular diffusers. McDonald [3] determined optimum geometries and performance data for conical diffusers. Sovran and Klomp [4] have performed investigation on annular diffusers and have come up with a classical map on these diffusers. Karanja and Sayers [5] have experimentally investigated the performance of wide angle diffuser with varying diffusion angle. The flow leaving the diffuser is usually non- uniform due to presence of adverse pressure gradient along the flow that enhances the development and separation of the flow from the walls of the diffuser. In case of wide angle diffuser this phenomenon is further aggravated due to the rapid increase of cross section areas in these diffusers or by achieving the area ratio in a short length. Mehta [11] has studied the effect of using the end screens at the exit of these diffusers for making the flow well suited for the wind tunnels. Sahin and Ward [12] and Sahin, et. Al. [13] have studied the performance of wide angle diffusers with perforated plates for the use in certain flow devices. Strand, et.al. [7] have used both PIV and LDV flow measuring systems to investigate the separated flow in a plane asymmetric diffuser and tried to see the feasibility of using numerical techniques with different turbulent models. Mahalakshmi, et. al. [14] have found that type of inlet distortion and angle of cone have a significant effect on flow structure with in a diffuser. Mehidi, et. al. [15] have investigation concerning velocity distribution downstream of a asymmetric wide angle diffuser and have concluded that an asymmetric diffuser needs more flow control devices at its exit so as to make the flow suitable for the downstream elements of the fluid flow system Separation can be avoided or delayed by using either perforated plates [7], wire gauzes [6], screens [8], vortex generators [10], star distorters [12] or struts [13]. The present investigation mainly aims to experimentally investigate the effect of area ratio and the diffusing angle on the performance of asymmetric rectangular wide angle diffusers. |
II EXPERIMENTAL FACILITY AND INSTRUMENTATION |
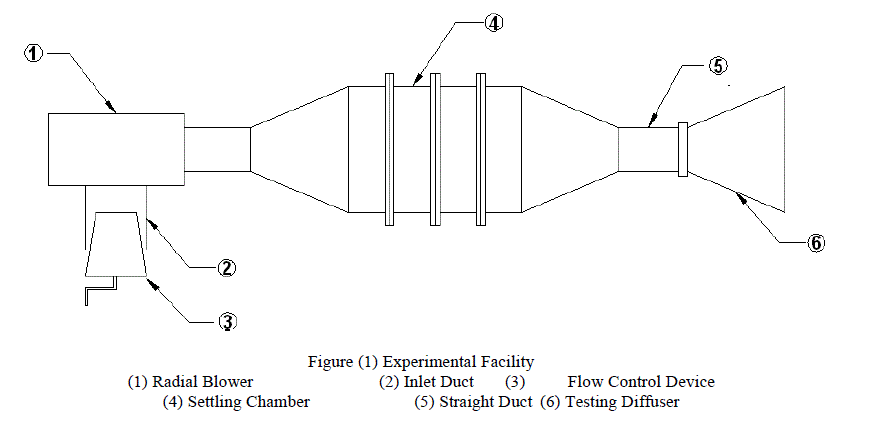
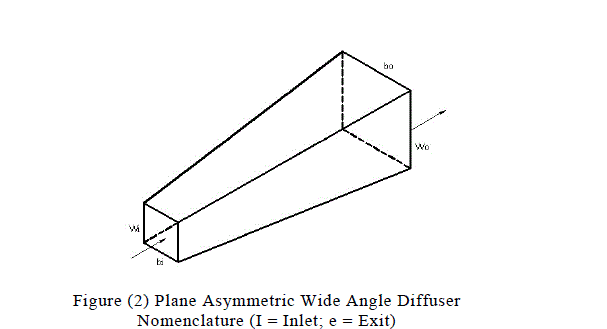
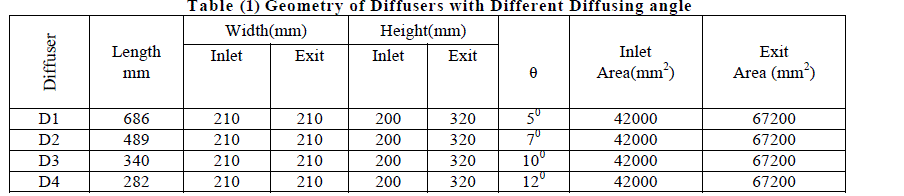
| The experimental facility, figure (1), is build around a radial blower of 3.5 kW power, pressure rise of 3.5 kPa and a flow rate of 0.83 cubic meters per second. The blower speed was 3450 rpm. The blower is fitted with an inlet duct of 200mm internal diameter and 300 mm length. The inlet duct has a cup and cone valve at the free end to control the flow rate through the diffuser. A circular duct of diameter 270 mm is fitted at the exit of the blower. The duct is connected to a settling chamber. The settling chamber has three parts. The inlet part is of diffusing section with inlet of diameter 270 mm where as its exit is rectangular of size 680mm x 600 mm. This diffusing section is connected to the middle part which is further divided into three portions of size 680mm x 600 mm and length 190 mm. These parts are connected tightly and wire gauze is fitted at each connection to decrease the turbulence of the flow. The exit of the settling chamber is a rectangular converging duct of inlet size 680mm x600mm and exit of size 220mm x 210mm. The converging section is connected to a small straight rectangular duct of size 220mm x210mm and length 200 mm. All the ducts are made from sheet metal. The diffusers are fitted at the end of the straight rectangular duct. The diffusers were fabricated from Perspex sheet of 8mm thickness. The diffusers discharge the air to the atmosphere. The diffusers were asymmetric having parallel roof and floor with diverging side walls. The overall error of parallelism of roof and floor (measured at several locations from inlet to exit) was ± 1.5 mm. The error in the divergence angle from top to the bottom of the diffuser was ± 0.250. The edges at the entry to the diffuser were properly smoothened by fine file and smooth sandpaper. The straight and diffuser sections were bolted through matching flanges and joined using chloroform. Figure (2) shows the definition diagram of straight wide angle rectangular asymmetrical diffusers. The geometrical details of the diffuser are given in table (1) and table (2). Karanja and Sayers [5] and Wolf and Jhonston [14] opine that the presence of a diffuser reconfigures the flow upstream of it. Therefore traverses of velocity probe were carried out upstream of the diffuser and a location was found where the velocity profile would match the normal velocity profile in a rectangular duct which was found at a distance of 1.75 times the width of the diffuser. This was taken as a free stream location for all the diffusers tested. The measurement of velocity profile at this location yielded almost a uniform velocity profile although the passage of the diffuser except very near the wall. The average free stream velocity values for various Reynolds numbers at which detailed testing was carried out is given in table (3). In the present study two precaliberated velocity probes were used for obtaining the velocity variations, in vertical direction, at the exit and the inlet of the diffuser. The diffusers were tested in a situation so that the parallel walls of the diffuser formed the roof and floor and the side walls were diverging. During the measurements of velocity at the exit of the diffuser the probe at the inlet was kept at the top most position so that it does not generate vortices that could alter and degenerate the flow at the exit of the diffuser. The wall static taps were fitted to the floor of the diffuser and the adjacent side diverging wall in such a manner that remained in flush with walls. The uncertainty of pressure and velocity measurements was ± 2.7% and ± 1.5 % respectively |
 |
 |
 |
III RESULTS AND DISCUSSION |
| Variation of Velocity at the Inlet and Exit of Diffuser: Wide angle diffusers have found widened use in many flow systems therefore it is important to understand the flow within these. The variation is plotted in terms of the velocity ratio VR with non dimensional width for different diffusers and at various Reynolds numbers. Velocity ratio VR is the ratio of the velocity at any location at the inlet or the exit of the diffuser to the mass averaged velocity at the inlet Vi for a diffuser. The mass averaged velocity is given as |
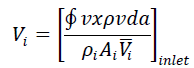 |
| The variation of this nondimensionalised velocity along the nondimensionalised width has is presented separately for showing the effect of diffusing angle and area ratio of diffuser with angle of 70. The full lines depict the variation of this non dimensional total velocity at the inlet whereas the dashed lines represent the non dimensional total velocity variation at the exit of the diffuser. The velocity variations at both the locations have been examined at five Reynolds numbers ranging from 22.3x105 to 23.7x105 but the results are presented only for one Reynolds number where as the discussion pertains to all the Reynolds numbers. |
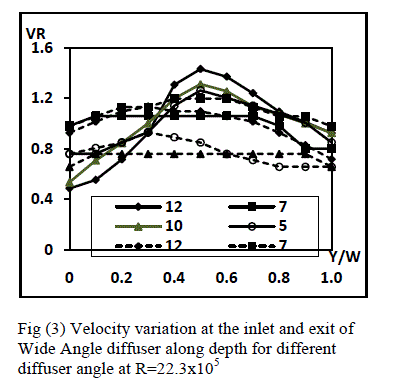
| Effect of Diffusing Angle: Figure (3) presents the variation of total velocity at the inlet and exit of different wide angle diffusers with angle of diffuser of 50, 70,100 and 120. In these diffusers it is found that the velocity ratio decreases from the midpoint of to the diffusers to the bottom and the top of the diffuser. The steepness of the velocity profile is more on the bottom side of the diffuser as compared to the upper side of the diffuser passage. The steepness of the velocity profile in the upper half of the diffuser increases with the increase in the diffuser angle. The inlet velocity profiles are almost equally steep on upper and bottom half of the diffuser width. The exit velocity profiles show lesser variation along the width of the diffuser. the variations of the velocity profile are more predominant in 120 diffuser and least in 70 diffuser. The standard deviation at the inlet varies from 10% to 35% (with respect to mass averaged velocity at that location) in all the diffusers for all the Reynolds numbers whereas it varies from 5% to 25% at the exit. This typical character of 70diffuser is also found in many other studies such as [15, 7]. It can be attributed to the fact that the better diffusing angle for a diffuser is 70, less than this value will increase the path length of the flow or the diffuser length, whereas more than this value would result in excessive separation beyond the inlet of the diffuser that would cause flow degradation and as a consequence a deficit in the performance of diffuser would be observed. |
| The variation of average velocity ratio VRa for different diffusers is presented in figure (4). The average velocity ratio becomes unity for the inlet profile as it should be but the exit profile changes at lower values of Reynolds number and then remains constant for higher values of the Reynolds numbers. |
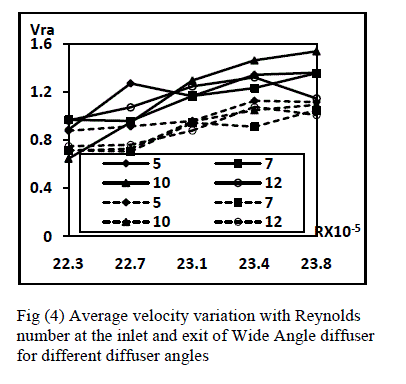
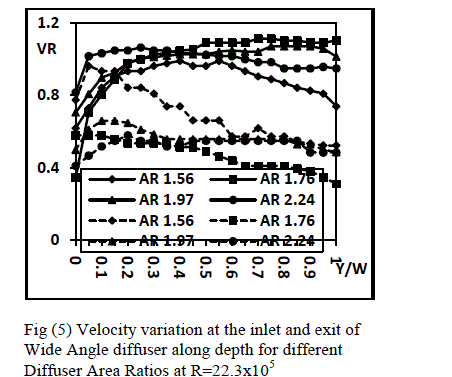
| Effect of Area ratio: Figures (5) present the variation of velocity ratio VR at the inlet and the exit of these diffusers. In these diffusers it is evident that the velocity ratio at the inlet of these diffusers decreases toward the bottom face of the diffuser and velocity tries to smoothen out towards the top face of the diffuser. The linearity is more evident at higher Reynolds numbers and also for diffusers with higher area ratio. At lowest Reynolds number the steepness of the velocity profile is more on the bottom face of the diffusers as compared to the upper face of the diffuser passage. At the inlet a consistent mild steep in the velocity profile is also observed in all the diffusers after y/W = 0.1. The variation in the area ratio of the diffuser shows a little variation at the velocity profile magnitudes along the height of the diffuser. At the exit as expected the variation in the velocity is high but the steep for all the diffusers is evident more near the bottom face of the diffuser. For most of the passage height the velocity is more or less uniform for any diffuser particularly for diffusers with area ratio 1.97 and 2.24. The variation between the diffusers is large which seems due to the difference in the flow behavior within these diffusers due to enlargement of the passage length. The magnitude of velocity along the length of the diffusers increases with the increase in area ratio from 1.56 to 1.76 and then decreases. As the Reynolds number increase the velocity at the inlet of diffusers becomes non uniform and becomes centric whereas the velocity at the exit of the diffuser become almost uniform for most of the height of the diffuser except at the bottom side of the diffuser where it falls. Most changes in the flow pattern are observed at the inlet of diffusers for the highest Reynolds number. |
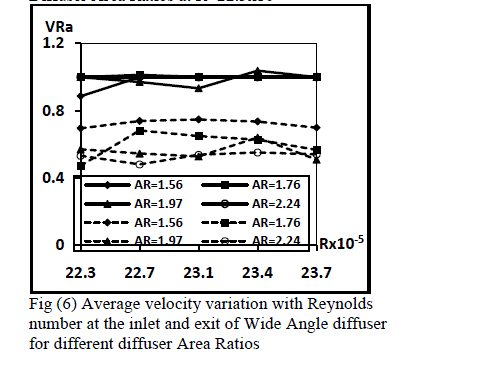
| The variation of average velocity ratio along the diffuser length for different Reynolds numbers is shown in figure (6). The average velocity ratio for all the diffusers tested under his category shows increases with the increase in the Reynolds number. The average velocity ratio at the inlet of the diffusers increases as the area ratio of the diffusers increase from AR=1.56 to AR=2.24. At the exit the variation of average velocity amongst the diffusers is small at low Reynolds numbers whereas a little variation is observed at lower Reynolds numbers. The average velocity increases steeply as the Reynolds number increases. |
 |
Flow Uniformity at Diffuser Inlet and Exit |
| The uniformity of flow in a flow passage is assessed by using distortion index, distortion coefficient, RMS percentage values, relative variation of velocity εv and blockage factor Bf. The distortion index and distortion coefficient methods are used in the cases when a physical nonuniformity situation is created, artificially or in real situation, at the inlet of the flow passage. Ariga, et al [16] have used this distortion index as the criteria for measuring the inlet flow distortion. O' Neil and Wickle [17] has used concept of shock loss for the same. Wright, et al. [18] proposed this factor in terms of total pressure loss coefficient. Salim [19] has used these techniques in a radial blower. This study uses relative standard error, RMS percentage index and blockage factor to see the nature of flow at the inlet and exit of each diffuser. Blockage factor is defined at a location as the ratio of blocked area by the reverse flow to the actual area of the passage at that location. It can be calculated either through actual boundary layer calculations [20] or from actual velocity profiles [21] or total and static pressure measurements [22]. In this study the method of [21] has been adopted It is defined as |
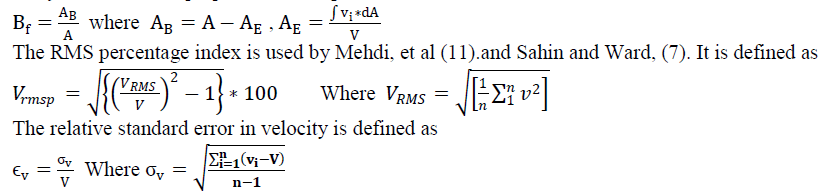 |
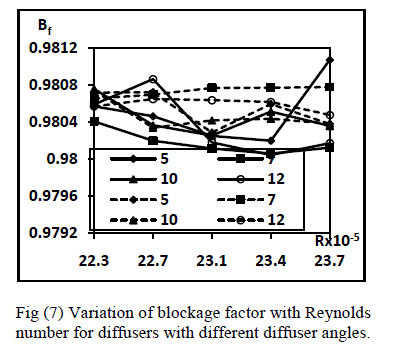
| The values of the blockage factor of the four diffusers for five Reynolds number at their inlet and exit are presented in figures (7, 8). The variations show that the blockage factor is least for diffuser with 70 diffuser angle both at the inlet and the exit of the diffuser. Blockage factor shows a tendency of decrease with increase in area ratio of the diffuser. |
| Figure (9, 10) shows the variation of RMS percentage index Vrms with the Reynolds number for different wide angle diffusers. Except at lowest Reynolds number for 120 diffuser the, at inlet, variations shows that the values of this index increase with the increase in Reynolds number for all diffusers tested. For the case of exit of the diffuser the index values progressively increase with the increase in the Reynolds number. This depicts that the inlet and exit flow from the wide angle diffusers loose uniformity as the Reynolds number is increased particularly for the diffuser with higher values of wide angle. It is evident from the variation that the index values do not show a fixed trend at inlet even though mostly an increasing nature with the diffuser angle for most of the lower Reynolds numbers is seen that is followed by a decreasing nature of variation. At the exit the RMS index values for all Reynolds number remains almost invariant with diffuser angle but the 70 diffuser showing slightly lesser values at all Reynolds numbers. Further index values increase with the increase in the Reynolds number. The RMS index shows a decreasing trend with the increase in area ratios of the diffuser. |
| Figure (11, 12) demonstrates the variation of the relative variation of total velocity εv with Reynolds number for different wide angle diffusers. The variation of εv at the inlet are not linear and do not have any explicit trend but more or less it can be argued that the variation of the velocity at the inlet of the diffusers increase as the Reynolds number increases but in show a decrease at highest Reynolds number tested. Further the variations decrease as the diffuser angle increase. The relative variation at the inlet of the diffuser shows the variations in the total velocity for a Reynolds number increases with increase in the diffuser angle except that the variations for diffuser with diffuser of angle 70 shows slightly lesser values than the other diffusers. The corresponding variations at exit location of the diffusers depict very small relative variations changes with the increase in the diffuser angle. Further the variations for a diffuser increase with the increase in the Reynolds number. The relative variations in the total velocity are more effected by the diffuser angle rather than the area ration of the diffuser. |
 |
PERFORMANCE EVALUATION |
| In diffusers flow takes place in presence of adverse pressure gradients which causes flow separation from its walls. This phenomenon results in total pressure loss. Other parameters that are important are static pressure rise coefficient or pressure recovery coefficient, diffuser efficiency and wall static pressure rise coefficient. Pressure recovery in a diffuser is caused by the deceleration of the flow as a consequence to its geometric enlargement of the flow area. The relationship of the performance to the geometry of the diffuser has been covered by Reneau, et al.(24 ), Kline , et al.(15), Sagi and Jhonston (25) and Japikse(30). The performance coefficients for a diffuser are defined as under. |
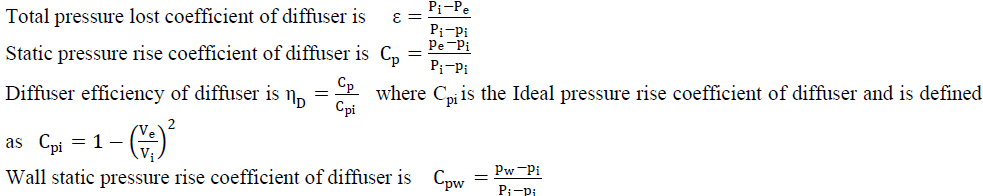 |
| Variation of Total Pressure Loss Coefficient: The total pressure loss coefficient is an indication of flow behavior within the diffuser. If the flow behaves well and flow passage is void of eddies and separation then total pressure loss will be minimum. Figures (13) and (14) depict the variation of total pressure loss coefficient for diffusers with different diffuser angles and area ratio respectively. The variation show that the total pressure loss coefficient has lower value for diffuser of 70 diffuser angle at most of the Reynolds numbers except at lowest Reynolds number value of 22.3x105 for which the lowest value is observed for 100diffuser. The reason is that the 100 diffuser behaves well at this lowest Reynolds number and at higher values of Reynolds number it experiences internal flow redistribution that causes in separation of flow within the diffuser resulting in higher value of total pressure loss coefficient in this diffuser. Diffusers with diffusing angle of 50 and 100 show higher variations at lower Reynolds numbers where as 70 and 120 diffusers depict lower values of variation with the Reynolds number. It is observed from the variation that the total pressure loss coefficient decreases as the Reynolds number increases and it is more for lower area ratio diffusers. |
| Variation of Pressure Recovery Coefficient: The pressure recovery coefficient or static pressure rise coefficient is an indication of the deceleration of flow in the diffuser. Variation of pressure recovery coefficient Cpr with the Diffuser angle and are ration is given in figures (15) and (16) respectively. These figures depicts that that Cpr is consistently higher for the diffuser with 70 diffuser angle for all the Reynolds numbers except for diffuser of 100 diffuser angle which has higher value of Cpr at lowest Reynolds number of 22.3x105. Further in comparison to other Reynolds numbers the pressure recovery increases is higher for Reynolds number22.7x105. Also the Diffuser with higher area ratio show higher values of pressure recovery compared to the lower area ratio diffusers. The total pressure loss coefficient represents the adverse flow situations in the diffusers. The disturbances are caused by the separation of the flow from the adjacent walls of the diffusers, mixing phenomenon along the diffuser passage and attachments of the flow later along the passage of the flow. |
| Variation of Diffuser Efficiency: Diffuser effectiveness includes both the geometrical and the fluid dynamical parameters. Japikse (23) has opined that the diffuser effectiveness serves as the parameter for showing the performance of a conical diffuser up to an area ratio of 20, beyond this area ratio the diffuser effectiveness and the pressure recovery has to be considered separately. In case of unsymmetrical diffusers this upper limit of the area ratio is drastically reduced. The diffuser efficiency for the diffusers is shown in figure (17) and figure (18). The diffuser efficiency of diffuser with diffusing angle of 70 is found higher than all the other diffusers at all the Reynolds numbers. The diffuser efficiency of this diffuser along with that of 120 diffuser increases with the Reynolds number where as for the rest it decreases with the increase in Reynolds number. This nature of variation can be attributed to the better flow situation in this diffuser due to the optimum nature of its diffuser angle. Japikse (30) reports better effectiveness of the diffuser with diffuser angle of 70 and length to width ratio of 25. This is also due to lesser variations in the inlet velocity of this diffuser which is also corroborated by Jhonston and Powars (12). As regards the effect of area ratio diffuser efficiency seems to be more influenced by the Reynolds number than the area ratio of these diffusers. The variation with area ratio is found only at lower Reynolds numbers and it rises with Reynolds number in all the diffusers with different are ratio. |
| Variation of Wall Static Pressure Coefficient:The wall static pressure as read through wall taping was nondimensionalised by subtracting mass averaged static pressure at the inlet of the diffuser at that Reynolds number and dividing the result by the dynamic pressure at diffuser inlet. In these figures the full lines show the variation of wall static pressure along the parallel wall whereas the dashed lines are drawn to present situation along diverging wall. Figure (19) and figure (20) show the variation of maximum values of the wall static pressure in different diffusers with the Reynolds number. The variation also indicates consistent increase of maximum wall static pressure with the Reynolds number and 70 diffuser showing higher values for all the Reynolds numbers. Further the horizontal parallel wall shows higher values for all maximum wall static pressure as compared to the diverging vertical wall of the diffusers. The better performance of diffuser with 70 diffusing angle is attributed to lower blockage factor for this diffuser. Further for the diffusers, with the change in the area ratio of the diffuser, the maximum value of wall static pressure shows a decreasing trend with the increase in Reynolds number. |
 |
 |
 |
IV CONCLUSIONS: |
| The following conclusions are drawn for this study. |
| 1. Blockage factor is least for diffuser with 70 diffuser angle both at the inlet and the exit of the diffuser and it shows a tendency of decrease with increase in area ratio of the diffuser. |
| 2. At the exit the RMS values for all Reynolds number remains almost invariant with change diffuser angle . Further its values increase with the increase in the Reynolds number and it shows a decreasing trend with the increase in area ratios of the diffuser. |
| 3. The relative variations in the total velocity are more effected by the diffuser angle rather than the area ration of the diffuser. Further the variation in the total pressure loss coefficient decreases as the Reynolds number increases and it is more for lower area ratio diffusers. |
| 4. The pressure recovery coefficient is consistently higher for the diffuser with 70 diffuser angle for all the Reynolds numbers. Also the diffuser with higher area ratio show higher values of pressure recovery compared to the lower area ratio diffusers. |
| 5. The diffuser efficiency of diffuser with diffusing angle of 70 is found higher than all the other diffusers at all the Reynolds numbers. Diffuser efficiency seems to be more influenced by the Reynolds number than the area ratio of these diffusers. |
| 6. The horizontal parallel wall shows higher values for maximum wall static pressure as compared to the diverging vertical wall of the diffusers.Further for the diffusers, with the change in the area ratio of the diffuser, the maximum value of wall static pressure shows a decreasing trend with the increase in Reynolds. |
| ACKNOWLEDGEMENT: This project was supported by Deanship of Scientific Research and Research Center College of Engineering, King Saud University, Riyadh, KSA. |
References |
|