Effect of Rotation on Marangoni Convection
in a Relatively Hotter or Cooler Liquid Layer

A. K. Gupta; D. Surya

Effect of Rotation on Marangoni Convection in a Relatively Hotter or Cooler Liquid Layer

A. K. Gupta¹, D. Surya²

Professor, Department of Mathematics, Himachal Pradesh University Centre for Evening Studies, Shimla, India
Research Scholar, Department of Mathematics & Statistics, Himachal Pradesh University Summer Hill, Shimla, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The effect of Coriolis force on the onset of surface tension driven convection in a relatively hotter or cooler liquid layer confined between two horizontal boundaries in the presence of uniform rotation is considered theoretically. The modified linear stability analysis is performed to obtain the eigenvalue system of eighth order. A Fourier series method is used to obtain the characteristic value equation analytically for the Marangoni number M which is then computed numerically. It is established that the rotation has stabilizing character irrespective of whether the liquid layer is relatively hotter or cooler.

Keywords

Conducting, Convection, Linear stability, Stationary, Surface tension.

I. INTRODUCTION

The phenomenon of the onset of surface tension induced convection in a thin horizontal liquid layer heated from below with free upper surface was first established experimentally by Block [1] and theoretically by Pearson [2]. They established that the patterned hexagonal cells observed by Bénard [3, 4], and explained by Rayleigh [5] in terms of buoyancy (discussed in detail by Chandrasekhar [6]), were in fact due to temperature dependent surface tension. Convection driven by surface tension gradients is now commonly known as Bénard-Marangoni convection, in contrast to buoyancy driven Rayleigh-Bénard convection. Bénard-Marangoni convection has received a great deal of research activities because it has many applications in geophysics, oceanography, atmospheric sciences, chemical engineering of paints and detergents. Quantitative disagreement between experiment and theory has indicated that gravity was present in Bénard’s experiments as well as in other experiments involving convection in a fluid layer with free surface in a laboratory on the earth, therefore, Nield [7] considered the combined effects of surface tension and buoyancy on the onset of convection in a fluid layer heated from below with free upper surface and found that the two effects causing instability reinforce one another and that as the thickness of the fluid layer decreases, the surface tension effects become more dominant. Further contributions made by many researchers namely, Scriven and Sternling [8], Smith [9], Davis [10] and Takashima [11, 12] have refined Pearson’s model by incorporating more realistic conditions. For a detailed study of Bénard-Marangoni convection one may be referred to the work of Normand et al. [13], Koschmieder [14] and Schatz et al. [15].

II. RELATED WORK

The onset of Bénard-Marangoni convection in a relatively hotter or cooler liquid layer has been analyzed by Gupta and Shandil [16] and established that irrespective of the thermal nature (conducting or insulating) of the lower boundary, the critical Marangoni number significantly depends on whether liquid layer is relatively hotter or cooler, and hotter the liquid layer more the postponement of the onset of convection. In view of the stabilizing nature of rotating fluids, a fact that has already been established by Chandrasekhar [6] for the buoyancy driven convection, by Vidal and Acrivos [17] for the surface tension driven convection and by Namikawa et al [18] for the convective instability induced by both surface tension and buoyancy. In the present study, therefore, we consider theoretically the possible influence of such a Coriolis force on the onset of convection driven by surface tension in a relatively hotter or cooler liquid layer. A Fourier series method is used to obtain the characteristic value equation analytically. The numerical results are obtained for a wide range of values of the Taylor number Ta. It is shown numerically that both the critical Marangoni number Mc and the critical wave number ac increase monotonically with Ta for a fixed value of the parameter 2T0 where T0 and  being the appropriately chosen mean temperature and coefficient of specific heat (at constant volume) variation due to temperature variation respectively of the fluid layer.

III. FORMULATION OF THE PROBLEM

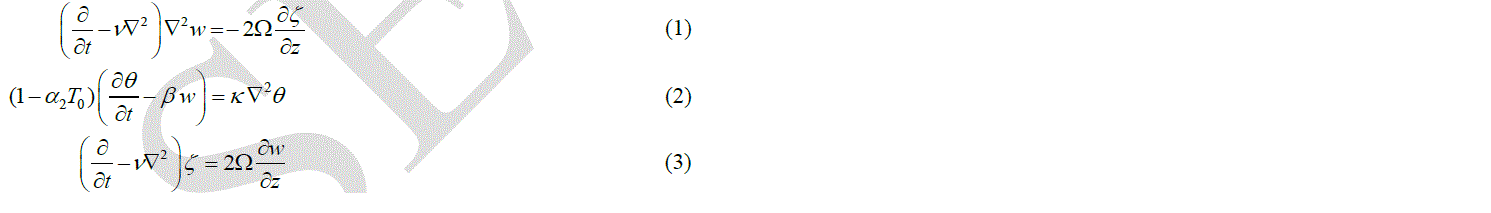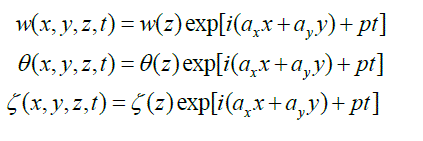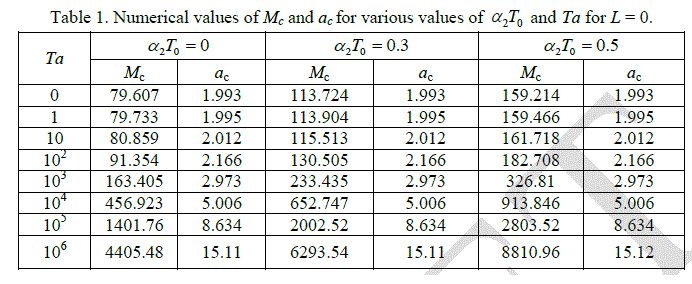
surface tension driven convection is concerned. Values of critical Marangoni number c M and the critical wave number ac computed from equation (38) are listed in Table 1 for assigned values of 2T0 and Ta when L = 0.

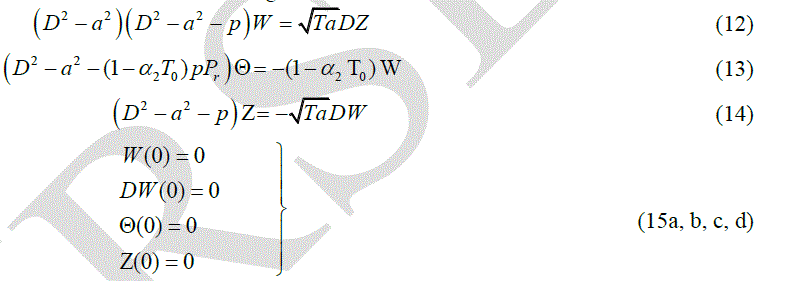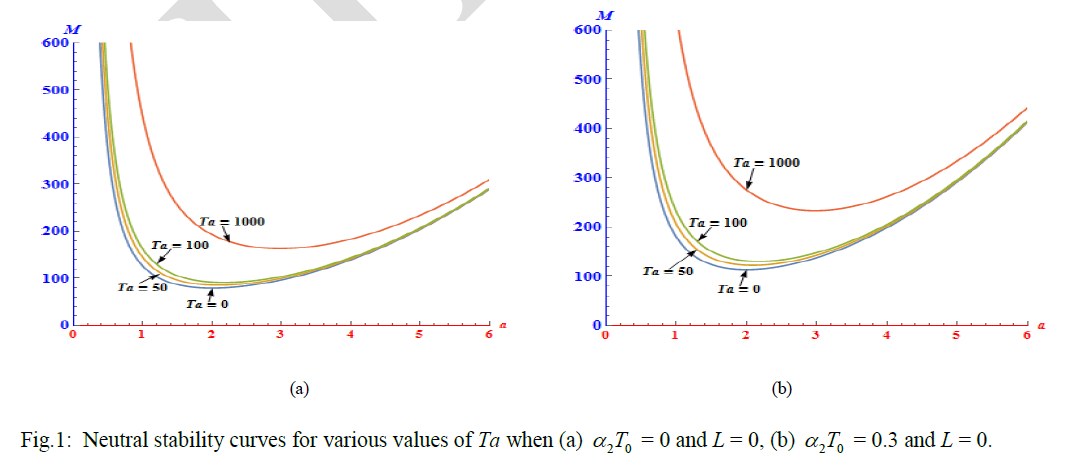We observe that there is smooth increase in the value of Mc with increase in value of Ta, clearly showing the stabilizing effect of Ta, irrespective of whether the liquid layer is relatively hotter (α2T0 = 0.3 ) or cooler ( α2 T0 = 0 ).

References

M.J. Block, “Surface tension as the cause of Bénard cells and surface deformation in a liquid film”, Nature, vol.178, pp.650-651, 1956.
J.R.A. Pearson, “On convection cells induced by surface tension”, J. Fluid Mech., vol.4, pp.489-500, 1958.
H. Bénard, “Les tourbillons cellulaires dans une napple liquid”, Revue général des Sciences pures et appliqués, vol. 11, pp.1261-1271, 1900.
H. Bénard, “Les tourbillons cellulaires dans une napple liquide transportant de la chaleur par convection en régime permanent”, Annales de Chimie et de. Physique, vol. 23, pp. 62-144, 1901.
L. Rayleigh, “On convection currents in a horizontal layer of fluid, when the higher temperature is on the underside,” Phil. Mag., vol.32(6), pp.529-546, 1916.
S. Chandrasekhar, “Hydrodynamic and Hydromagnetic Stability”, London: Oxford University Press, 1961.
D. A. Nield, “Surface tension and buoyancy effects in cellular convection”, J. Fluid Mech., vol.19, pp.341-352, 1964.
L.E. Scriven and C.V. Sternling, “On cellular convection driven by surface tension gradients: effects of mean surface tension and surface viscosity”, J. Fluid Mech., vol.19, pp.321-340, 1964
K.A. Smith, “On convective instability induced by surface tension gradients”, J. Fluid Mech., vol.24(2), pp.401-414, 1966.
S. H. Davis, “Buoyancy-surface tension instability by the method of energy”, J. Fluid Mech., vol.39(2), pp.347-359, 1969.
M. Takashima, Surface tension driven instability in a horizontal liquid layer with deformable free surface: I. Stationary convection, J. Phys. Soc. Jpn., vol.50, pp.2745-2750, 1981(a).
M. Takashima, “Surface tension driven instability in a horizontal liquid layer with a deformable free surface. II. Overstability,” J. Phys. Soc. Jpn. vol.50, pp.2751–2756, 1981(b).
C. Normand, Y. Pomeau and M. Velarde, “Convective instability: a physicists approach,” Rev. Mod. Phys., vol.49, pp.581-624, 1977.
E.L. Koschmieder, “Bénard cells and Taylor vortices,” Cambridge: Cambridge University Press, 1993.
M.F. Schatz, S.J. VanHook, W.D. McCormick, J.B. Swift and H.L. Swinney, “Onset of surface tension driven Bénard convection,” Phys. Rev. Lett., vol.75, pp.1938-1941, 1995.
A.K. Gupta and R.G. Shandil, “Marangoni convection in a relatively hotter or cooler liquid layer”, Proc. Natl. Acad. Sci., India, Sect. A Phys. Sci., vol.28(2) pp.103-106, 2012.
Vidal and A. Acrivos, “The influence of Coriolis force on surface tension-driven convection”, J. Fluid. Mech.., vol.26(4), pp.807-818, 1966.
T. Namikawa, M. Takashima and S. Matsushita, “The effect of rotation on convective instability induced by surface tension and buoyancy”, J. Phys. Soc. Jpn., vol.28(5), pp.1340-1349, 1970.