EFFECT ON DISPLACEMENT COMPONENTS
DUE TO FREE BOUNDARY AND RIGID
BOUNDARY IN CASE OF DEFORMATION OF
A UNIFORM HALF-SPACE CAUSED BY A
VERTICAL TENSILE FAULT

Mahabir Singh; Ravinder Kumar Sahrawat; Minakshi; Meenal Malik

EFFECT ON DISPLACEMENT COMPONENTS DUE TO FREE BOUNDARY AND RIGID BOUNDARY IN CASE OF DEFORMATION OF A UNIFORM HALF-SPACE CAUSED BY A VERTICAL TENSILE FAULT

Mahabir Singh,¹ Ravinder Kumar Sahrawat,² Minakshi³and Meenal Malik⁴

CoE, Department of Administration, Deenbandhu Chhotu Ram University of Science and Technology, Murthal, India
Assistant professor, Department of Mathematics, Deenbandhu Chhotu Ram University of Science and Technology, Murthal, India.
Research Scholar, Department of Mathematics, Deenbandhu Chhotu Ram University of Science and Technology, Murthal, India.
Assistant Professor, Department of Mathematics, A.I.J.H.M. College, Rohtak, India.

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Closed form analytical expressions for the stresses and displacements are derived caused by a long vertical tensile fault buried in a homogeneous, isotropic, perfectly elastic half-space with rigid boundary. The Airy stress function approach has been used to calculate stresses and displacements at an arbitrary point of the half-space. The variation of the displacement field with the horizontal distance from the fault and with the depth is studied numerically and the results obtained in the case of rigid boundary are compared with that of free boundary.

Keywords

Deformation, Long Tensile Fault, Airy Stress Function, Rigid Boundary.

INTRODUCTION

Steketee (1958) and Okada (1985) have applied the theory of dislocation to seismological problems. To understand the deformation or dislocation, the two dimensional models are very useful. Such models are developed by Maruyama (1964), Rybicki (1971), Freund and Barnett (1976) and Davis (1983). In contrast to the progress that has been made in the modeling of the deformation field due to free boundary the studies related to rigid boundary are scarce.

In the present paper, the results of Singh and Garg (1986), Rani et al. (1991) and Singh and Singh (2000) are of direct relevance. These researchers applied the traction-free boundary conditions at the surface of half-space. Malik et al. (2012), Malik et al. (2013) and Malik and Singh (2013) obtained the results by considering the source buried in a half- space with rigid boundary. Following the work of above researchers, the airy stress function for a long tensile fault of finite width has been obtained in the present paper and the expressions for stresses and displacements at any point of the half-space with rigid boundary caused by a long vertical tensile fault are derived using the relations between stresses and displacements given by Sokolnikoff (1956).

The tensile dislocations are often employed to many seismic events like magma intrusion, dykes injection, mine collapse and study of fluid driven cracks.

THEORY

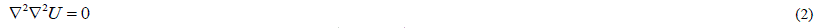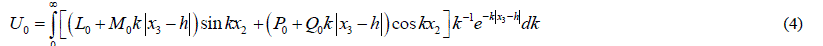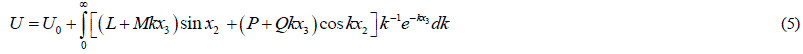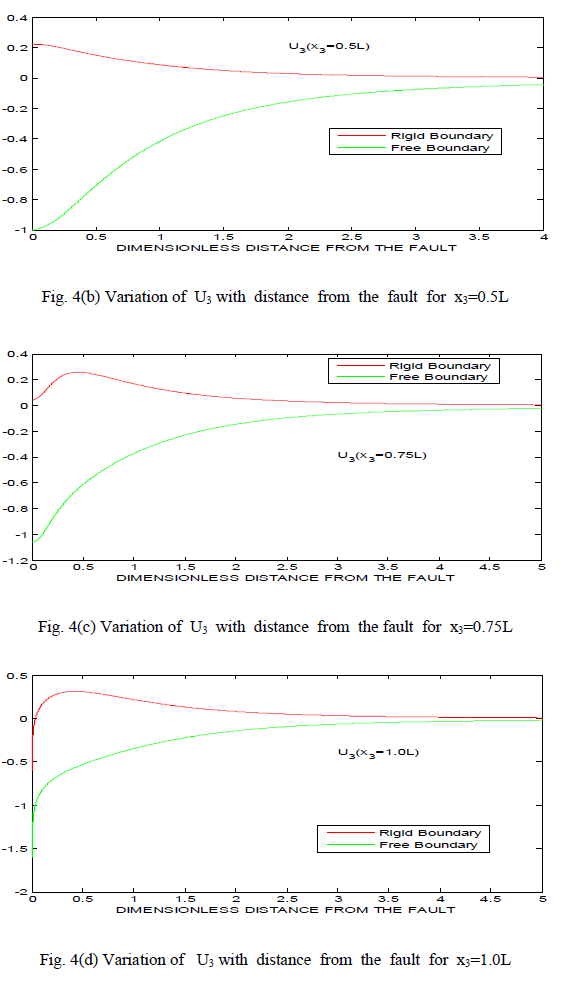
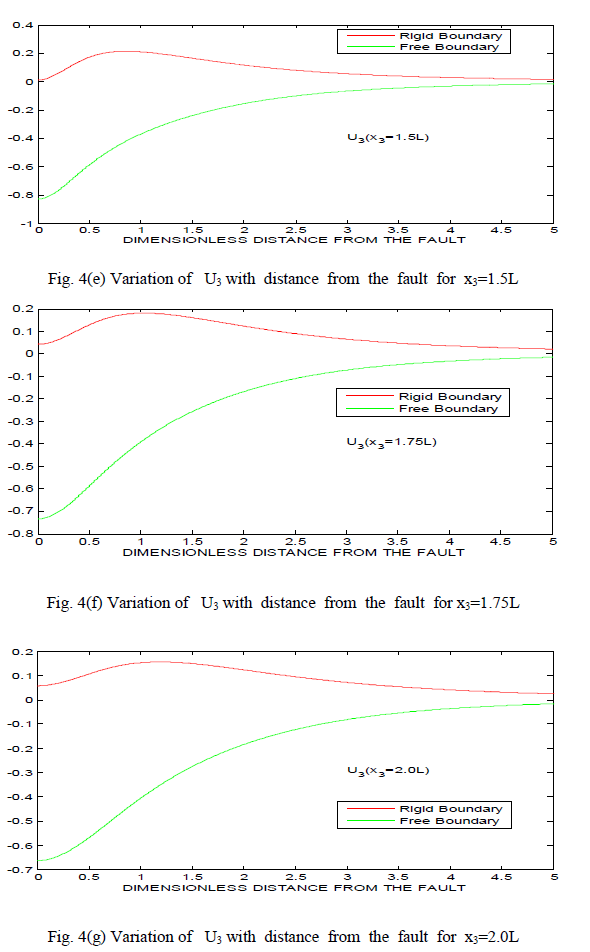
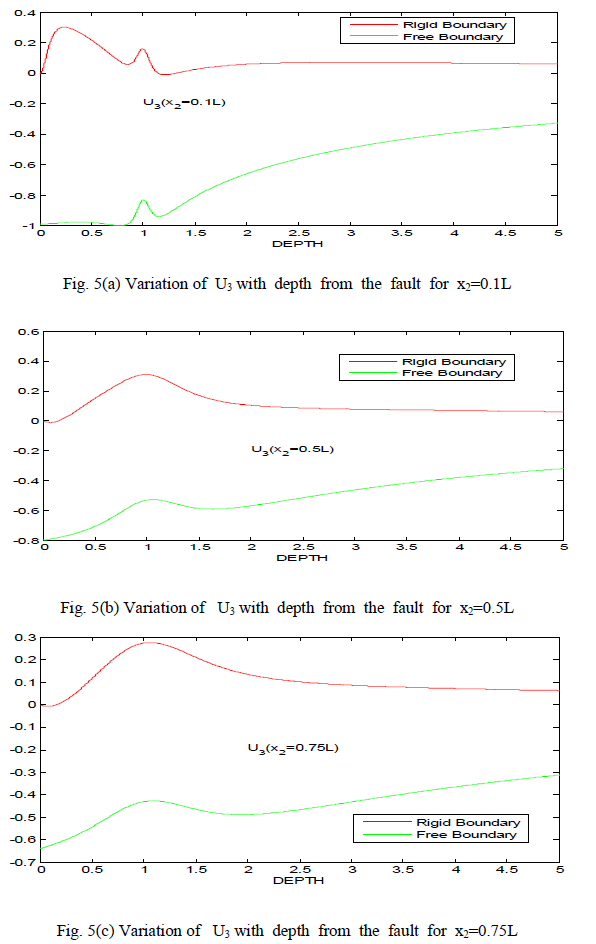
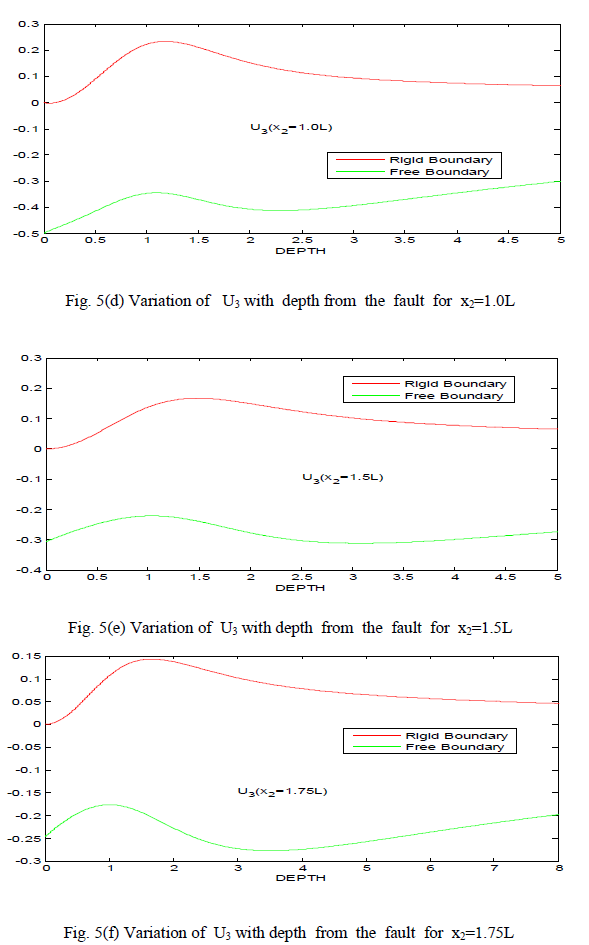
IV. DISCUSSION

V. CONCLUSION

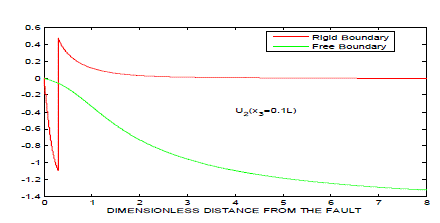
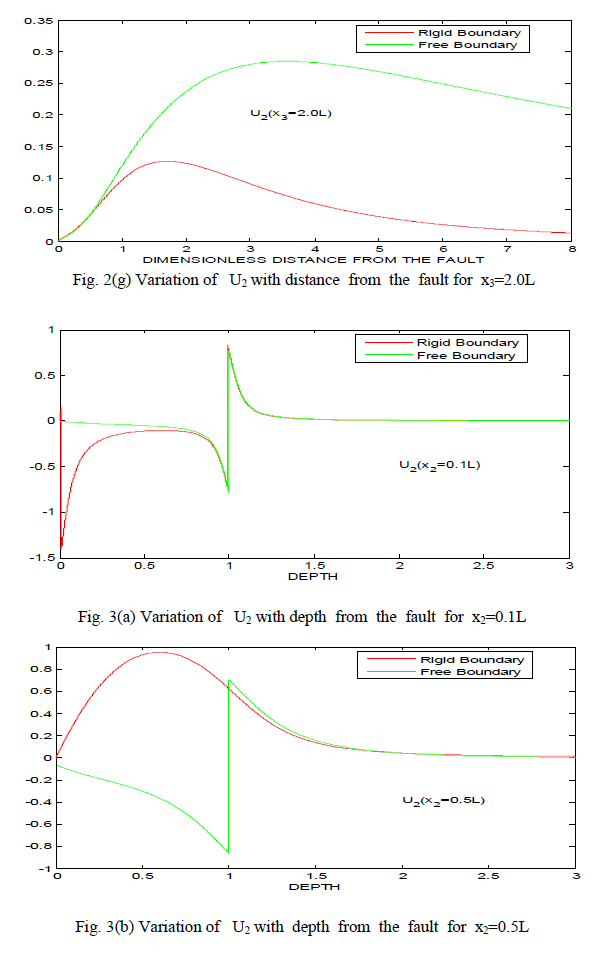
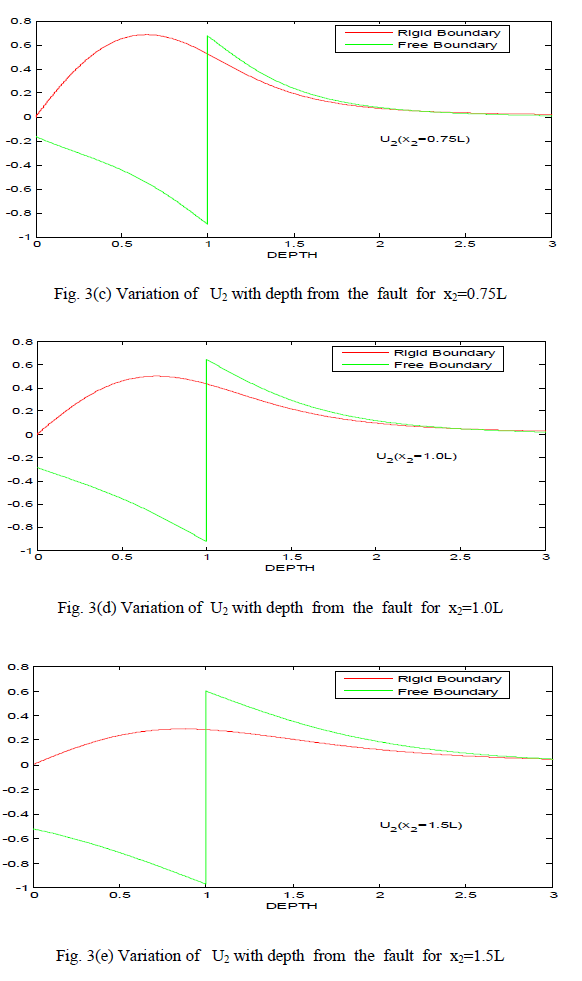
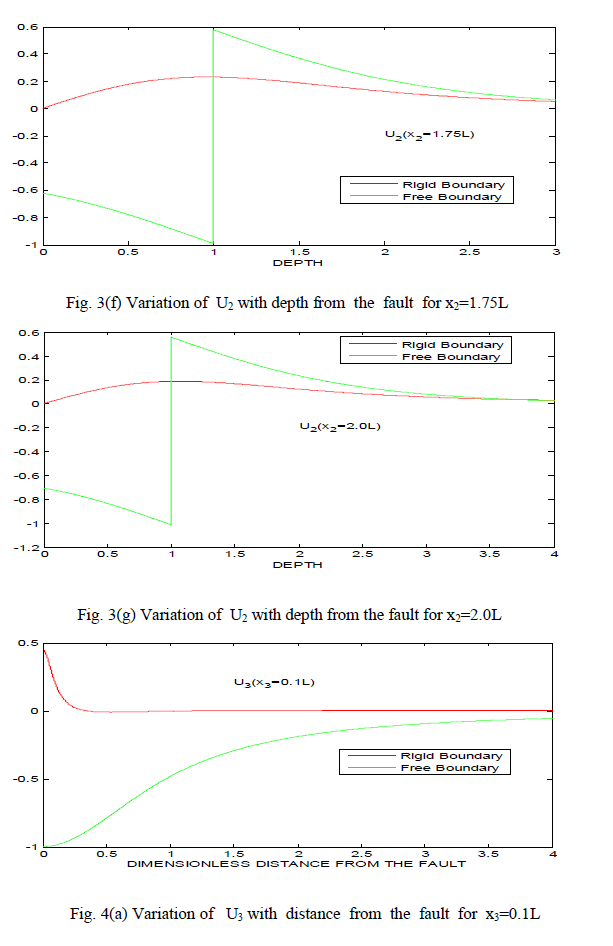
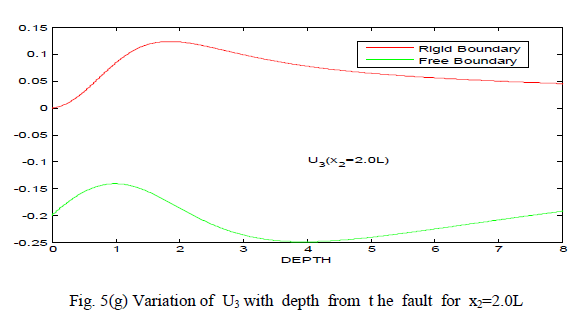
1. The displacement components U2 and U3 have no negative values for almost all values of x2 and x3 in case of rigid boundary where as they have mixed sign in case of free boundary.

2. There is a sudden change in the value of U2 at x3=L in case of free boundary and similar behaviour appears near origin (0<x2<L) in case of rigid boundary.

3. The variation of U2 and U3 is smooth for both the cases of free boundary and rigid boundary, when values of x2 and x3 are infinitely large.

APPENDIX

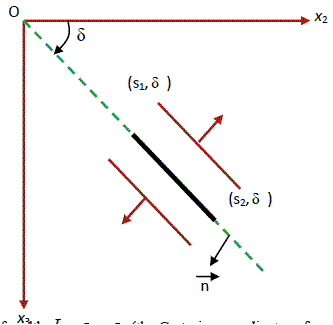
In case of vertical dip-slip fault, the positive sign is for x3  h and the negative sign is for 3x  h , b is the magnitude of the displacement dislocation and ds is the width of the fault.

References

Davis, P. M., “Surface deformation associated with a dipping hydrofracture”, J. Geophys. Res.,vol. 88, pp. 5826-5834, 1983.
Freund, L. B. and Barnett D. M., “ A two-dimensional analysis of surface deformation due to dip-slip faulting”, Bull. Seismol. Soc. Am., vol. 66, pp. 667-675, 1976.
Malik, M. and Singh, M., “Deformation of a Uniform Half-Space with Rigid Boundary Due to a Strike-Slip Line Source”, IOSR Journal of Mathematics, vol. 5, pp. 30-41, 2013.
Malik, M., Singh, M. and Singh, J., “ Static Deformation of a Uniform Half-Space with Rigid Boundary due to a Dip-slip on 450 Dipping Fault”, Journal of Computing Technologies, vol.1, pp. 26-34, 2012.
Malik, M., Singh, M. and Singh, J., “Static Deformation of a Uniform Half-Space with Rigid Boundary due to a vertical Dip-slip Line Source”, IOSR Journal of Mathematics, vol. 4, pp. 26-37, 2013.
Maruyama, T. , “ Statical elastic dislocations in an infinite and semi-infinite medium”, Bull. Earthq. Res. Inst., vol. 42, pp. 289-368, 1964.
Okada, Y. , “ Surface deformation due to shear and tensile faults in a half-space”, Bull. Seismol. Soc. Am., vol. 75, pp. 1135-1154, 1985.
Okada, Y. , “ Internal deformation due to shear and tensile faults in a half-space”, Bull. Seismol. Soc. Am., vol. 82, pp. 1018-1040, 1992.
Rani, S. , Singh, S. J. and Garg, N. R., “ Displacements and stresses at any point of a uniform half-space due to two-dimensional buried sources”, Phys. Earth Planet. Inter., vol. 65, pp. 276-282, 1991.
Rybicki, K., “ The elastic residual field of a very long strike-slip fault in thr presence of discontinuity”, Bull. Seismol. Soc. Am.,vol. 61, pp. 79-92, 1971.
Singh, S. J. and Garg, N. R., “ On the representation of two-dimensional seismic sources”, Acta Geophys. Pol.,vol. 34, pp. 1-12, 1986.
Singh, M. and Singh, S. J., “ Static deformation of a uniform half-space due to a very long tensile fault”, ISET J. Earthq. Techn., vol. 37, pp. 27-38, 2000.
Sokolnikoff, I. S., “ Mathematical theory of elasticity” ; McGraw-Hill, Newyork, 1956.
Steketee, J. A., “ On Volterra’s dislocations in a semi-infinite elastic medium”, Can. J. Phys., vol. 36, pp. 192-205, 1958a.
Steketee, J. A. , “ Some geophysical applications of the elasticity theory of dislocations”, Can. J. Phys., vol. 36, pp. 1168-1198, 1958b.