International Journal of Innovative Research in Science, Engineering and Technology
MenuISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
B.R Sharma1, Kabita Nath2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The effects of viscous dissipation, Joule heating and chemical reaction on demixing of a binary mixture of incompressible viscous electrically and thermally conducting fluids in two dimensional steady boundary layer flow with temperature dependent viscosity and thermal conductivity due to a continuously moving surface under the influence of weak uniform transverse magnetic field is investigated. The momentum , energy and concentration equations are reduced to non-linear coupled ordinary differential equations by similarity transformations and are solved numerically by using MATLAB’s built in solver bvp4c. These numerical results are exhibited graphically from which it has been found that the effects of various parameters are to separate the components of the binary mixture by collecting the lighter and rarer component near the surface of the plate and throwing the heavier one away from it. The effects of various parameters on the local skin friction, the Nusselt number and the Sherwood number have been shown in tabular form.
Keywords |
| Viscous dissipation, Chemical reaction, Demixing, Binary mixture. |
INTRODUCTION |
| Processes of separation of the components of an electrically conducting binary mixture of incompressible viscous fluids under the influence of magnetic field are considered to be of significant importance due to their applications in many engineering problems such as nuclear reactors and those dealing with liquid metals. This frequently occurs in agriculture, engineering, plasma studies and petroleum industries. The problem of free convection under the influence of the magnetic field has attracted the interest of many researchers in view of its applications in geophysics and astrophysics. The MHD has also its own practical applications. For instance, it may be used to deal with problems such as the cooling of nuclear reactors by liquid sodium and induction flow meter, which depends on the potential difference in the fluid in the direction perpendicular to the motion and to the magnetic field. In many chemical engineering processes, chemical reactions take place between a foreign mass and the working fluid which moves due to the stretch of a surface. The order of chemical reaction depends on several factors. One of the simplest chemical reactions is the first order reaction in which the rate of the reaction is directly proportional to the species concentration. Chemical reaction can be classified as either homogeneous or heterogeneous processes, which depends on whether it occurs at an interface or as a single–phase volume reaction. In most cases of chemical reactions, the reaction rate depends on the concentration of the species itself. A reaction is said to be of first order if the rate of the reaction is directly proportional to the concentration. |
| Separation processes of components of a binary fluid mixture wherein one of the components is present in extremely small proportion are of much interest due to their applications in science and technology. Besides environmental engineering applications, convection mass transfer alone constitutes the backbone of many operations in chemical industry. Separation of isotopes in its naturally occurring mixture is one such example. The composition of binary mixture is described by the concentration C1, defined as the ratio of mass of rarer and lighter component to the total mass of the mixture in a given volume. The concentration C2 of heavier and abundant component is given by C2 = 1 – C1. A binary mixture subject to the temperature gradient can generate thermal diffusion i.e. the temperature gradients cause solute fluxes. This phenomenon is known as Soret effect. In the flow of such a mixture the diffusion of individual species takes place by three mechanisms namely concentration gradient, pressure gradient and temperature gradient. The diffusion flux ⃗ is given by Landau and Lifshitz [1] as: |
 |
| where ρ is the density of the fluid, Kp, D is the pressure diffusion coefficient and KT, D is the thermal diffusion coefficient. The ordinary diffusion contribution to the mass flux is seen to depend in a complicated way on the concentration gradient of the components present in the mixture. |
| Sakiadis [2] studied the boundary layer flow over a stretching surface moving with constant velocity, while Tsou et al. [3] ascertained experimentally the results of Sakiadis by analyzing the effects of heat transfer on a continuously moving surface with constant velocity. Whereas, Soundalgekar and Murty [4] studied the heat transfer problem by assuming the plate temperature to be variable.Sakiadis work was again extended by Erickson et al. [5] to include suction or injection at the stretching sheet on a continuously moving surface with constant speed and investigated its effects on the heat and mass transfer in the boundary layer region. Pop et al. [6] obtained similarity solutions by considering viscosity as an inverse function of temperature and assuming constant velocity and temperature of the plate. Howell et al. [7] and Rao et al. [8] studied the momentum and heat transfer on a continuous moving surface in a power law fluid. Kumari and Nath [9] discussed the problem of MHD boundary layer flow of a non-Newtonian fluid over acontinuously moving surface with a parallel free stream. Fang [10] studied similarity solutions of thermal boundary layer for a moving plate. Soundalgekar et al. [11] investigated the flow of incompressible viscous fluid past a continuously moving semi-infinite plate by considering variable viscosity and variable temperature. Ibrahim et al. [12] studied the combined effect of wall suction and magnetic field on boundary layer flow with heat and mass transfer over an accelerating vertical plate. Makinde [13] analysed the magnetohydrodynamics boundary layer flow with heat and mass transfer over a moving vertical plate in the presence of magnetic field and a convective heat exchange at the surface with the surrounding. Makinde et.al [14] studied the effect of temperature dependent viscosity on free convective flow past a vertical porous plate in the presence of a magnetic field, thermal radiation and a first order homogeneous chemical reaction. Recently Jat et al. [15] studied hydromagnetic flow and heat transfer on a continuously moving surface. He has studied the effect of parameters such as reference temperature, exponent, magnetic, Prandtl number and Eckert number on heat transfer. Sharma and Singh [16, 17, 18], Sharma and Nath [19] and Sharma et al. [20, 21] studied the effect of magnetic field on demixing of a binary fluid mixture. Sharma and Singh [22, 23] studied the effect of temperature gradient on demixing of species in hydromagnetic flow of a binary mixture of incompressible viscous fluids between two parallel plates, first taking the plates horizontal and second by taking the plates vertical. They found that the effect of temperature gradient is to separate the components of the binary mixture and the magnetic field increases the effect of species demixing. Geetha et al. [24] studied MHD boundary layer flow of heat and mass transfer on a continuously moving surface with chemical reaction. |
| In this piece of work we investigate the effect of variations of viscosity and thermal conductivity on separation of the components of an electrically and thermally conducting binary mixture of incompressible viscous fluids set in steady motion due to a continuously moving surface under the influence of weak uniform transverse magnetic field. |
MATHEMATICAL FORMULATION |
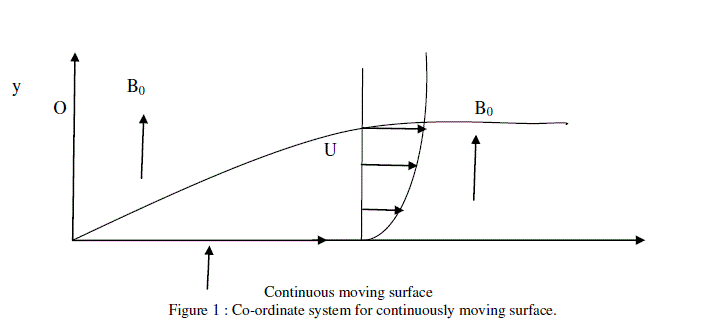
| We consider the separation of a binary mixture of a chemically reacting electrically conducting incompressible viscous fluids in a two-dimensional steady boundary layer flow past a continuously moving surface with uniform velocity U in presence of a weak uniform transverse magnetic field of strength B0 by taking the x-axis along the surface and y-axis normal to it as shown in Figure. 1. The magnetic Reynolds number is assumed to be small so that the induced magnetic field can be neglected. It is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible. All the fluid properties are assumed to be constant, except for the fluid viscosity and thermal conductivity which are assumed to be inverse linear functions of temperature, Lai and Kulacki [25], as given by |
 |
 |
 |
RESULTS AND DISCUSSION |
| Since the solutions of the set of non-linear coupled ordinary differential equations (18) – (20) under the boundary conditions (21) cannot be obtained in a closed form therefore we have solved these equations numerically with MATLAB’s built in solver bvp4c. |
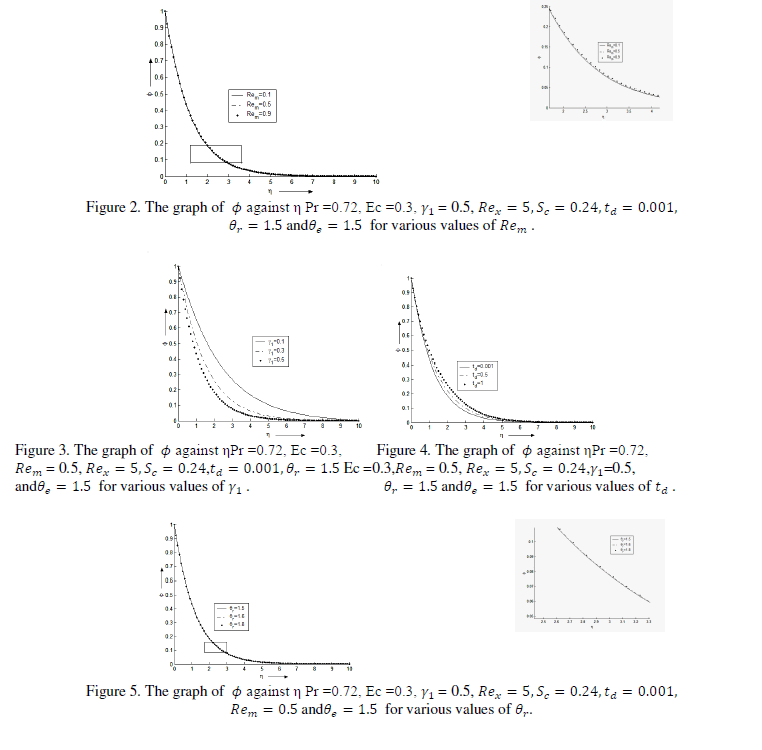
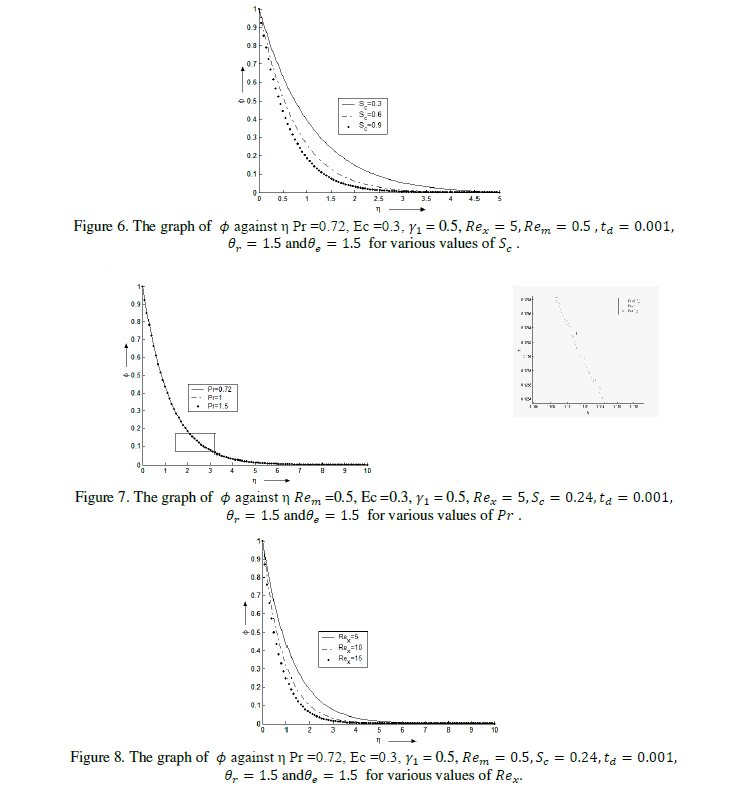
Numerical calculations have been carried out for concentration of the rarer and lighter component
of the binary fluid mixture for various values of the parameters and are
plotted against η in Figures 2-10. The Prandtl number is taken to be Pr = 0.72, which corresponds to air, the value of
Schmidt number (Sc ) is chosen to be 0.24 that represents diffusing chemical species of most common interest in air
like H2. |
| Figures 2 to 10 show that the concentration of the rarer and lighter component of the binary mixture is more at the surface of the plate and decreases exponentially as η increases to 5. After then in the region η > 5 no variation inθ is observed. It is observed from the figures that the separation of the binary mixture takes place mostly in the region 0 < η < 5 and thereafter separation is found to be negligible. |
 |
 |
 |
 |
 |
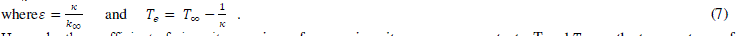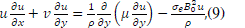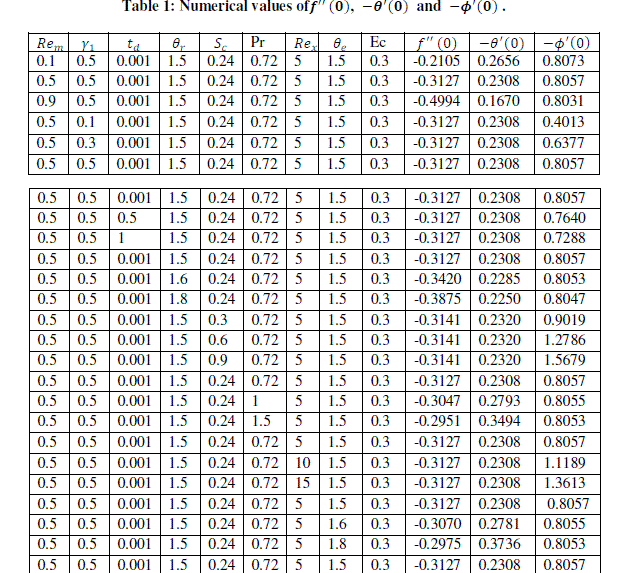
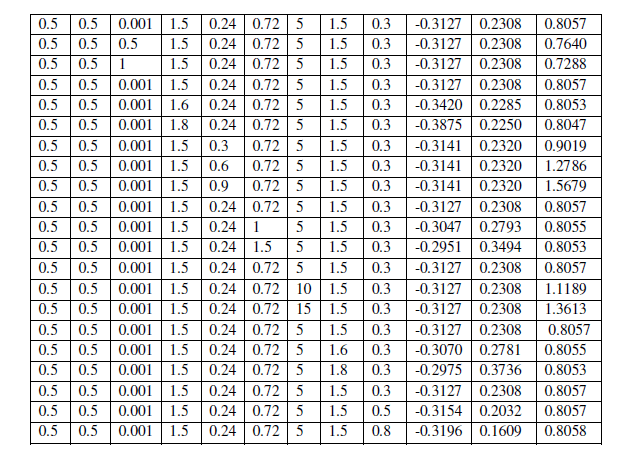
| Finally, the effects of the local skin friction, the Nusselt number and the Sherwood number are tabulated in Table 1. The behaviours of these parameters are self – evident from the Table 1 and hence any further discussion about them seems to be redundant. |
 |
 |
ACKNOWLEDGEMENT |
| This research work is funded by grants from the UGC, New Delhi, India (File No. 39-43/2010 (SR)) as a Major Research Project awarded to Dr. B. R. Sharma. Kabita Nath is associated with the project as a Project Fellow. The authors are grateful to UGC for providing financial support during the research work. |
References |
|