Electric and Magnetic Properties of Semiconductors and Metals in One, Two and Three Dimensions

Abstract

The detailed theoretical study of some of the interesting electric and magnetic properties in low dimensions have been discussed. The 2D hydrogen atom problems has been solved and the energy eigen values are obtained and compared with the 3D values. The polarization value is obtained in both 2D and 3D cases using Dalgarno and Lewis method. The present result we obtained exactly coincides with others results. Some electronic properties like density of states and specific heat capacity for one, two and three dimensions have been studied and this clearly shows that it depends on temperature. The magnetic property like paramagnetic susceptibility for one, two and three dimensions have been obtained and the result shows that it is independent of temperature in all cases.

Keywords

Semiconducting materials, Metals, paramagnetic substance

INTRODUCTION

A Semiconductor is a substance which has very few free electrons at room temperature. Consequentlyunder the influence of potential difference a semiconductor practically conducts no current. At low temperature the valence band is completely full and conduction band is completely empty. Therefore a semiconductor behaves as an insulator at low temperature. As the temperature is increased more valence electrons cross over to the conduction band and the conductivity increases. This shows that the electrical conductivity of the semiconductor increases with the rise in temperature.

Elements of group III-V, II-VI are combined together in the presence of impurity to form compound semiconductor. Examples of III-V group compound semiconductors are GaP, InP, InSb, InAs and GaAs. Examples of II-VI group compound semiconductors are ZnS, CdS.GaAs is the most familiar example used for both high speed electronics and for opto electronic devices.

Physics of low dimensionalsystem has been a topic of interest from the theoretical point of view for a long time. This is mainly due to the fact that simple models are amenable for an exact solution from which more complicated results may be interpreted.

Real electrons are 3D but can be made to behave as though they are free to move in fewer dimensions. This can be achieved by trapping them in a narrow potential well that restricts their motion in one dimension to discrete energy levels.If the separation between these energy level is large enough the electron will appear to be in frozen into the ground state and no motion will be possible in this dimension. The result is a 2D electron gas. The same effect can be achieved wih a 2D potential well which leaves the electron free to move in 1D only as a quantum wire.

Metals have a unique property which distinguishes them from other materials. They are very good conductors of electricity. When an electric field is of very feeble strength is applied, it causes an electrical current in the metal, which is apparently a result of the drift of electrons in one direction. At absolute zero of temperature in the absence of an applied field all those states are fully occupied which lie within the Fermi surface. This is symmetrical about the origin and hence for every electron with an average velocity there is another with equal and opposite average velocity. So the net current is zero.

II. TWO DIMENSIONAL HYDROGEN ATOM

2.1SOLUTION TO SCHRODEINGER’S EQUATION

The 2D hydrogen atom consists of an electron revolving about a nucleus in a circular orbit. The hydrogen atom problem is a two body problem which involves the motion of two particles (nucleus and electrons) that are attracted to each other by a force that depends on the distance between them. The Schrodeinger’s equation for 2D hydrogen atom can be written as

Since the centre of mass of the system moves like a free particle of mass ‘m’ and the equation of relative motion of the two particles is the same . The equation for the motion of the particle that has reduced mass in an external potential field V(r) we shall consider it as aond body problem.

The wave function is given by

Substituting and simplifying we get,

Comparing the coefficients of the different powers of ρ yields the Recurrence relation,

Finally we get

2.2POLARIZABILITY USING DALGARNO LEWIS METHOD

2.2.1 Polarisation of 3D hydrogen atom

The second order Starck effect can be interpreted in terms of an induced dipole moment. The induced dipole moment is proportional to the applied electric field and the same direction and the ratio α of dipol moment to field strength is called polarisability. It is easily seen that these conditions hold exactly for a charged isotropic harmonic oscillator and the energy change in this case is -1/2αE2.

W2 = -1/2αE2

Also W2= -9/4E2a03.

Comparing we get ,α = 9/2a03.

For a 3D hydrogen atom in the ground state , the polarisability can be found out using Dalgarno Lewis method are as follows.

The second order energy correction W2 is given by ,

The ground state wave function of 2D hydrogen atom is

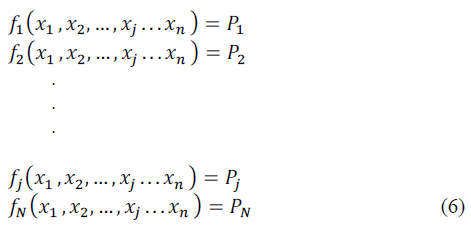The second order energy correction is

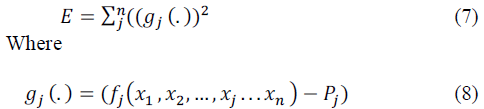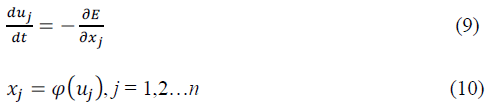Substituting we get , W2 = -9/4 c2

W2 = (-9/4) E2 a0 3 , a0 is the Bohr radius.

W2 = -1/2αE2. = (-9/4) E2 a03

Thereforepolarisability α3D = 9/2 a03

2.2.2 Extension to two dimension

W2 = (-21/512) E2 a03

Thereforepolarisability α2D= (-21/256* 1.414) a03

Hence α2D / α3D= 1.3 x 10-2 ,which agrees well with other works.

2.3DENSITY OF STATES

2.3.1 Density of states of an electron gas in 3D

Density of states is an important parameter which plays a major role in calculating various properties. It is defined as the number of states or orbital per unit energy range.

If N is the total number of orbital with energy ≤ E then the Density of states is ,

where n is the number of states or orbital per unit volume.

Energy is given by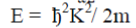

If Kf is the Fermi wave vector then the volume is ,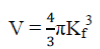

Simplifying we get ,Density of states at Ef is , D3 (Ef) = 1/α* C1/2Ef1/2

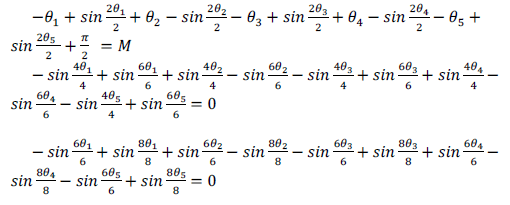2.3.2 Density of states of an electron gas in 2d

The expression for the Density of states of an electron gas can be divided in a similar way as the 3D provided the volume is replaced by area

D2 (Ef) = 2m/π?2

2.3.3 Density of states of an electron gas in 1D

The area of the Fermi surface in 2D is replaced by the radius of the Fermi sphere,

D1 (E) = 1/C E-1/2

2.4 SPECIFIC HEAT CAPACITY IN 3D

Specific heat capacity is defined as the amount of heat required to raise the temperature of unit mass of the substance through one kelvin.

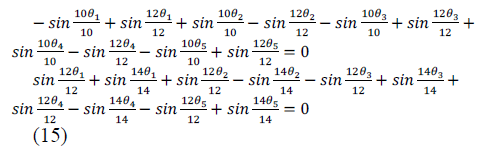Substituting and simplifying we get,

i.e., Cvα T , at temperature very muchlower than than Fermi temperature.

2.4.1 Extension to one and two dimensions

In 2D ,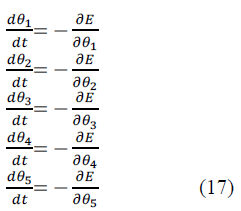

i.e., Cvα T, at low temperature

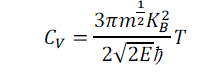From this it is concluded that the heat capacity at very low temperature is proportional to the temperature irrespective of the dimension.

2.5. PARAMAGNETIC SUSCEPTIBILITY OF CONDUCTION ELECTRONS

Classical electron theory gives an unsatisfactory account of the paramagnetic susceptibility of the conduction electrons. Experimental investigations shows that magneton of most normal non ferro magnetic metal is independent of temperature, violating curie’s law. The probability that an atom will be lined up parallel to be exceeds to probability of an antiparallel orientation roughing μb/KBT . For N atoms per unit volme this gives a net magnetization = Nμ2B/ KBT. Most conduction electrons in a metal have no possibility of turning over when a field is applied because most of the orbital in the Fermi sphere with parallel spin are already occupied. Thus only a fraction T/Tfof the total number o felectrons contribute to the susceptibility.

M =Nμ2B/ KBTf which is independent of temperature and of the observed order of magnitude. The concentration of electrons with magnetic moments parallel to the magnetic field is

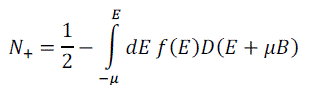The concentration of electrons with magnetic moments anti parallel to the magnetic field is

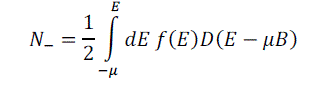The Magnetisation is given by

M = μ (N+ - N-)

In 3D paramagnetic susceptibility

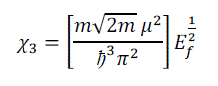In 2D paramagnetic susceptibility

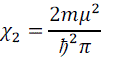In 1D paramagnetic susceptibility

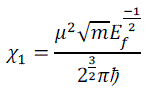From the three equations we infer that the paramagnetic susceptibility is a constant in 2D, which is proportional to E f1/2 in the 3D and is proportional toE f-1/2 in 1D, but is independent of temperature in all the three dimensions.

III. RESULTSAND DISCUSSIONS

In two dimensional hydrogen atom the main quantum number starts from zero which shows that it has a zero point energy whereas in 3D the main quantum number starts from one which indicates that there is no zero point energy. Also in 3D the binding energy of excited ground state is E0 but in 2D it is 4E0 . So the large binding energy in 2D can be understood by considering quantum well structure with decreasing width.

Comparison of eigen values in 2D and 3D hydrogen atoms.

The polarisability of 2D hydrogen atom is compared with the 3D hydrogen atom. We get the ratio of polarisability to be α2D / α3D= 1.3 *10-2which agrees well with other works. Though there has not been any work reported on the measurement of polarisability of any low dimensional system, there have been some estimates of donarpolarisability in a quantum well of GaAs / Ga1-xAlx As system. There estimates well made using variational methods. Our results are compared with these works in the following table. Polarisability estimates of a 2D hydrogenic system

The expression for density of states in one, two and three dimensions have been obtained. The results are D1(E) α E- 1/2 ,D2(E) = Constant and D3(E) α E1/2 respectively. Some electronic properties like density of states and specific heat capacity for one, two and three dimensions have been studied. Also in present work semiconductor systems like GaAs and CdTe and their densities corresponding to different energy levels have been considered and the results are shown in figure 1 and 2.

For different metals their specific heat corresponding to various temperature have been considered and their results are shown in figure 3 and 4.

The paramagnetic property for the susceptibility of conduction electrons for one, two and three dimensions have been studied. Also in present work, considering one of the paramagnetic substance like Al and their susceptibility corresponding to different energy levels have been studied and the results are shown in figure 5.

IV. CONCLUSIONS

The electric and magnetic properties in low dimensions have been studied and discussed theoretically in this work. The 2D hydrogen atom problems has been solved and the energy eigen values are obtained and compared with the 3D values . It is also found that the binding energy of the 2D hydrogen atom is four times that of the 3D case.The polarization value is obtained in both 2D and 3D cases using Dalgarno and Lewis method. Using this expression we obtained an exact result as that of others results (Sukumaranetal and Elangovanetal). Some electronic properties like density of states and specific heat capacity for one, two and three dimensions have been studied and this clearly shows that it depends on temperature. The magnetic property like paramagnetic susceptibility for one, two and three dimensions have been obtained and the result shows that it is independent of temperature in all cases.

ACKNOWLEDGEMENT

We are very thankful to honourable chairman Pro-chancellor, Vice Chancellor, Registrar, Dean R&D and Dean Engineering of Bharath University for their continuous support and encouragement given to carry out this research work

ACKNOWLEDGEMENT

We are very thankful to honourable chairman Pro-chancellor, Vice Chancellor, Registrar, Dean R&D and Dean Engineering of Bharath University for their continuous support and encouragement given to carry out this research work

Tables at a glance

Table 1 Table 2 Table 3 Table 4 Table 5

Figures at a glance

Figure 1 Figure 2 Figure 3 Figure 4 Figure 5

References

M.EI Said & M. Tamak, Phys. Rev B42,3129 (1990). B. Sukumar and K. NavaneethaKrishnan,Pramana J.Phys.35, 3129 (1990) A. Elangovan and K. Navaneetha Krishnan, Solid state communication 83,635 (1992). Ferry and Goodnik, Transport in semiconductor nanostructcres,II Edition. H.Haug and Sm. Koch, Quantum theory of optical and electronic properties of semiconductors. Vi.LeonardI.Schiff, Quantum mechanics, III Edition