International Journal of Innovative Research in Science, Engineering and Technology
MenuISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Utpal Deka1, Nayan Kamal Bhattacharyya2, Prem Das Chettri3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In presence of multicomponent ionic plasma, more than one plasma sound waves are possible depending on the number of ions. In this work, we considered the presence of a negative ion along with the normal positive ion. Here we show that finite but weak electron inertial delay effect causes a resonant excitation of the ion acoustic solitons near the transonic zone, which depends on e  i1,2  m m ratio. It has been seen that under such situation near the plasma sheath transonic zone, the KdV equations have complex coefficients. We have shown that even in presence of the complex coefficients soliton like solution can be derived only for infinitely long wavelength source perturbation. It is seen that when the negative ions mass becomes equal to that of a dust particle then similar excitation situation as in case of colloidal plasma can be retrieved. It is plausible that such kind of a resonant excitation may lead to acoustic turbulence near the plasma sheath edge. A detailed discussion of the nonlinear acoustic mode analyses in the transonic regime with negative ionic impurity using a hydrodynamic approach is presented
Keywords |
| Electron inertia, Transonic zone, Sheath edge, Nonlinear acoustic modes, Soliton, Multispecies plasma. |
INTRODUCTION |
The area of plasma sheath has been of active interest for the scientist and engineers for its wide scale application in
various branches of science and engineering [1 -3]. The physics of plasma sheath formation for normal two-component
plasma was put forwarded long back by Tonks and Langmuir [4] in 1929. The condition for sheath formation requires
that the ions drift speed should have velocity greater than the ion sound speed i.e. (k is the Boltzmann
constant, Te is the electron temperature and M is the ionic mass), at the sheath edge was given by David Bohm 1949 [5].
The problem of plasma sheath transition from quasi-neutral bulk plasma to the non-neutral and nonlinear plasma sheath
at the plasma wall boundary has been of great attention due to the presence of singularity at the plasma sheath edge in a
two scale model as pointed by Riemman [6]. In the two scale theory of presheath-sheath transition singularity arises
due to transition from a long scale (of the order of the half of the system length) to the sheath scale of the order of few
times of Debye length. To overcome this patching problem Riemann et. al. suggested a new concept of three scale
transition region with an introduction of an intermediate scale between the presheath and the sheath having an
intermediate length [7]. It is noteworthy to mention here that the one of the early pioneering work with an analytical
model in this regard was proposed by Self [8] in 1963. He tried to arrive at an exact solution for the Tonks and
Langmuir equation [4] for the plasma and sheath by using a series expansion method of the integral equation and
solved it numerically. Most of these theoretical models are self sufficient for particular situations and no universal
consensus was arrived.
There has been a significant work about the issue of singularity by various workers under different force field
configuration and compositions [9 – 13]. In spite of numerous and rigorous work done by various scientist, still this
area beholds with large resource for newer problems. The first author along with his other co-workers put forwarded a new concept of the formation of the sheath of the basis of wave turbulence model [14]. Though the concept is still in its
infancy but it gives a new dimension to the already going works about the plasma sheath transition problem.
An important aspect of all these theoretical models is that the electrons are always considered to be inertialess
compared to that of the ions because of the ions much heavier mass than that of the electrons, i.e. me /mi→0. But in the
last few years this concept has come under critical review [15 -21]. Such an assumption can hold good only for a cold
plasma (Ti << Te) and for non drifting ions i.e. for stationary ions. In case of drifting ions, when we analyse the
propagation of the ion acoustic wave in a moving frame of reference near the sheath entrance, which we can call as the
transonic zone also, the universal consideration of the Boltzmannian distribution of the electrons do not hold good. It
has been shown that when weak but finite electron inertial effect is considered than ion acoustic wave fluctuations of a
two-component plasma system with drifting ions reveals a new mode of instability [16]. Such type of instabilities can
be called as resonance mode instability, which will take place only when the plasma flow velocity exceeds the ion
acoustic speed of non-drifting plasmas. Such situations can be seen to exist in the transonic region of the plasma sheath
system and also in solar and other stellar wind plasmas. In fact, under such a situation the Debye sheath condition
formation also gets modified [19]. Under such assumption the collective degrees of freedom will be modified.
Thus, it is quite easily realizable that the nonlinear mode of the ion acoustic wave in the transonic zone in a bounded
plasma system also gets modified [15]. The modification of the nonlinear mode of the ion acoustic wave has been
shown in a two component plasma system along with the presence of colloidal particles [18]. The investigation of
solitary wave propagation in plasmas has gained lot of momentum since the discovery of ion acoustic soliton by
Washimi and Taniuti [22] described by the Korteweg–de Vries (KdV) equation. The laboratory verification of the
existence of acoustic solitons came four years later when Ikezi et al. [23] showed its existence in two component
plasma system. There has been some effort to investigate the effect of high energy drifting ions for propagation of
arbitrary‐amplitude solitary waves in plasma with and without the consideration of the inertial effect of the electrons.
Varieties of physical situations of drifting ions of high energy with [24, 25] and without inclusion of the electron inertia
motion have been considered for theoretical description of the ion acoustic soliton. Similar situations are practically
realizable in the magnetoshperic region of the earth. But in these studies the relativistic effect of the electrons were
considered. In these works it was mentioned that the existence of complex coefficients of the KdV equation as a
condition for non existence of the ion acoustic solitons. That‟s why the linearly unstable condition in the velocity
regime was excluded. But interestingly such condition hides some other interesting physical facts and condition for non
existence of solitary waves were refuted, which is reported in the literature as mentioned in Ref. [16].
In this work, we propose to see a similar effect with multi-component species. The existence of plasma with multicomponent
is naturally found in the magnetospheric region and the Van-Allen belts of the earth. Moreover, number of
experiments related to the ion acoustic waves in a multi-component and colloidal or dust plasma has been carried out in
the laboratory as reported in the literatures. But the ion acoustic wave propagation in a drifting ion beam system near
the transonic zone is yet to be done. Here we will present a theoretical study of the instability in the ion acoustic
fluctuations in a drifting ion beam system in presence of two different ionic species (with positive charge) due to weak
but finite electron inertial delay effect. Moreover the importance of solitons has wide range applications in
communications and other fields [26-28].
This paper is basically divided into four major sections including the introduction. In the next section we shall
elaborately present the physical model of the problem along with the detailed mathematical formulations. In the third
section we shall cover detail discussions about the results derived in the previous section. Finally in the last section the
conclusion of the work along with the scope for future direction will be presented. |
PHYSICAL MODEL AND MATHEMATICAL FORMULATIONS |
| In this work we shall show that a driven KdV equation can be derived for the steady-state behavior of the nonlinear normal mode of an acoustic wave under linearly unstable conditions of the spectral component as shown in [16]. We have considered a simple unmagnetized plasma consisting of three components with two positive ions of different having nearly equal masses, same degree of ionization but of different density along with electrons. The system is considered to be collisionless plasma in which the ions are drifting with uniform velocity at near supersonic speed. Further no extra sink or source terms are considered. The linear acoustic waves are resonantly excited due to weak but finite electron inertial delay effect. However, we made another assumption that the transonic zone near the plasma sheath edge has a finite extension. The primary excitation mechanism is based on the compressibility of the electrons, which otherwise becomes redundant Boltzmannian distribution for the electrons is considered. Moreover it is assumed that the plasma wall absorbs the plasma through surface recombination and the neutral particles get re-circulated into the bulk plasma. Under the hydrodynamic model the basic governing equations for the electron, the two ions and are discussed below. |
| The electron continuity equation is given below |
 |
 |
 |
 |
 |
 |
 |
 |
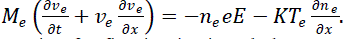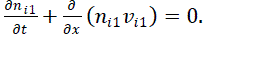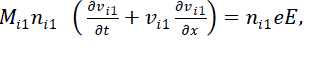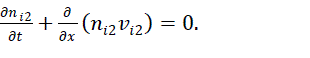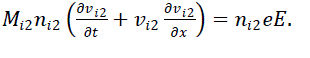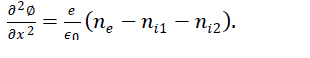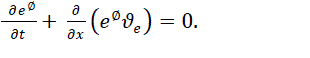RESULTS AND DISCUSSIONS |
| The above theoretical calculation is carried out for a special case of occurrence of multispecies plasma with drifting ions. We have analyzed the behavior of the nonlinear normal mode of the ion acoustic wave near the transonic zone signified by the condition of . 0 10 i k v . This is the condition of the resonant instability for the fluctuations to grow in a moving beam. In general, the unstable behavior of the propagation of soliton is not considered to exist under normal circumstances. In literatures as mentioned above, it has been mentioned that the existence of complex coefficients in the KdV equation should be a condition for non-existence of solitons. But contradictory to such assumptions we have shown with our theoretical work that solitary waves can still exist even though the coefficients may be complex. Under such condition it gives rise to a special situation in which we observed that the KdV equation has got a source term. This source term infact acts as the driving source for the instability. It is noteworthy to mention here that the modified form of the KdV equation has been derived by invoking the idea of global phase modification. With this new idea we have observed that nonlinear solution of the normal acoustic mode is possible, which may gives rise to solitary kind of waves. As discussed in the experimental section in Ref. [16], it is also possible that oscillatory shock like solutions may be possible under a steady state condition in the transonic zone. A more appropriate comparison can be given by doing a numerical integration of Eq. (64), which is similar to the results mentioned in Ref. [16]. The numerical integration has been left out as a future course of the work. The form of the driven KdV equation derived for our case of multispecies plasma is structurally same as that derived by the authors in Ref. [16]. We can reasonably defend that as soon as the solitary wave passes through the unstable transonic zone near the plasma sheath edge, it may experience transient phase modifications, which leads to the formation of an oscillatory shock. Under such a driving mechanism of the instability we can argue that there may be adiabatic rearrangement of the spectral components of the usual solitary wave. Now if we analyze the formation of such a driven KdV equation, which is possibly going to give rise to oscillatory shock like solitary wave solutions as mentioned in Ref. [16], the whole genesis lies in the inclusion of the finite but weak electron inertial effect. Henceforth, we can say that the linear growth of the instability is related to finite but weak electron inertial delay effect that is supposed to be active in the transonic zone. Since the form is same, we may expect the similar kind of numerical solution as derived for two-component plasma [16] system, where it was found that normal soliton structure was not retained and oscillatory solution was obtained. This theory can be extended by increasing the mass ratio and different Mach number. This work becomes a general description for a multi-component plasma system and can be easily extend to study for dust particles by changing the mass ratio. Numerical investigation of equation (64) or a complete simulation of equation (63) will give us more indepth physics about evolution of such acoustic waves. Further, this analysis gives us the idea that the plasma sheath edge is a rich zone where various wave activities are possible. Hence, there is a possibility of wave-wave coupling and particle-wave coupling. Under such condition wave turbulence activities cannot be denied, since to activate turbulence there must be some kind of instability in the system. So, it is permissible to hypothesize the idea of a wave turbulence model to describe the sheath formation, which should give a new dimension to the ongoing problem of the plasma sheath edge singularity. |
CONCLUSION |
| From the detailed analytical work about the investigation of the propagation behaviour of the nonlinear normal mode of the ion acoustic wave near the transonic zone of the plasma sheath in a multi-component plasma system, indicates that finite but weak electron inertia can act as a source for driving the acoustic mode unstable. The linear growth of such instability shows that solitary shock like solutions are possible inspite of the coefficients of the derived KdV equation becoming complex. We have justified with our analytical work that some new physics can be derived from such a situation. This type of instabilities can be well justified to be of the nature of resonant type instabilities, which leads to a global phase modification of the spectral components of the soliton. This will be wise to mention that more detailed information of the nature of propagation could have been arrived at by doing a complete simulation of the new KdV equation with the modified coefficients and the source term. Such kind of studies should help us to understand many such phenomena in the laboratory system with multispecies plasma or in the Earth‟s Van Allen belt or the auroral regions. Moreover we would like to suggest that the plasma sheath edge region should be a rich region where different wave activities are likely to occur leading to an exchange of energy between the wave and the particles, such that the ions can derive energy from the waves to enter the sheath region. |
References |
|