ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Saleem Ayaz Khan1*, Wilayat Khan1, Sikander Azam1, A. H. Reshak1,2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Full potential linear augmented plane wave based on density functional theory were applied for calculating the density of states, valence electron charge density and transport properties of Ba4LaGe3SbSe13. The exchange correlation potential was solved by Engel Vosko generalized gradient approximation. The calculated total density of states clarified that Ba4LaGe3SbSe13 acquire small band gap (1.60 eV). The calculated partial density of states show the role of orbital’s that forming the electronic bands. The evaluation of electronic charge density plot established the mixed ionic-covalent nature of the bonds. Both Se‒Sb and Se‒Ge are strong covalent bonds having 8.8 % and 10 % ionicity while the ionic behavior of Se‒La and Se‒Ba increase to 31.8 % and 37.3%. In additional the transport properties were calculated using the Boltzmann transport theory. The average tensor components of electrical conductivity, Seebeck coefficient, thermal conductivity and power factor were calculated discussed in details within temperature range between 100 K and 800 K. The power factor of Ba4LaGe3SbSe13 exposed that it is potential candidate for thermoelectric technological applications around 400 K. The second order dielectric tensor components (xx, yy and zz) of transport properties (conductivity, Seebeck coefficient, thermal conductivity and power factor) show considerable anisotropy.
Keywords |
| Semiconductor; Electronic structure; Electronic charge density; Transport properties |
INTRODUCTION |
| Thermoelectricity is the phenomenon of conversion between thermal and electrical energy. Compared with other technologies, thermoelectric (TE) devices offer distinct advantages: they have no moving parts, contain no chlorofluorocarbons, and have a long lifetime of reliable operation. However, current TE materials have found limited commercial application due to their low efficiency. TE efficiency is related to a material-dependent coefficient, Z, and is often expressed as the dimensionless figure-of-merit, ZT, given by ZT=σS2/K, where T is the absolute temperature, σ is the electrical conductivity, S is the Seebeck coefficient, and K is the total thermal conductivity. It becomes difficult to improve ZT beyond a certain point since the material properties S, σ, and K are interdependent [1]. Presently, simple bulk materials have reached an upper limit of ZT at approximately 1. Thermoelectric devices, allowing the solid-state conversion between thermal and electrical energy, have long been considered a very attractive technology for cooling and waste heat recovery. However, the low conversion efficiencies of actual thermoelectric devices have prevented them from entering most of their potential application markets. Over the last 15 years, advances in the fields of materials science and nanotechnology have restored an intense interest for such an energy conversion technology. Today’s main strategy to produce materials with high thermoelectric figures of merit is to trigger phonon scattering at multiple length scales without disturbing the charge carrier transport [2]. Among the most studied materials in thermoelectric research are ternary and higher antimony chalcogenides [3–12], bismuth chalcogenides [13–17], germanium and tin-based clathrates [18–21]. A particularly well explored family of high-temperature thermoelectric is (AgSbTe2)1-x(GeTe)x (TAGS) [22,23]. Based on this, we are currently investigating higher germanium antimony chalcogenides. While there are no analogous selenides known that comprise both Ge and Sb, a handful of selenogermanates as well as seleno-antimonates have been reported before. The former are often noncentrosymmetric and typically exhibit GeIVSe4 tetrahedra (e.g., Sr2GeSe4 [24], KLaGeSe4 [25], K2Hg3Ge2Se8 [26]), but trivalent (Sr2Ge2Se5) and divalent Ge selenides (Ba2Ge2Se5) are known as well [27]. Much more seleno-antimonates exist, which typically show irregular Se coordination of the SbIII atoms [28], comparable to Sb2Se3 [29]. Arguably the compound most comparable to the title compound Ba4LaGe3SbSe13 is the noncentrosymmetric quaternary silicon antimony selenide Ba4SiSb2Se11 [30] that show only little structural resemblance, if any. Assoud et al. [31] synthesized the first mixed seleno-germanate/antimonate, Ba4LaGe3SbSe13. Its structure composed of GeSe4 monotetrahedra and Ge2Se7 ditetrahedra. The latter are part of an almost linear unique anion of the composition [Ge2Se7–Sb2Se4– Ge2Se7]-14, where in weak Sb–Se interactions connect the central centrosymmetric Sb2Se4 unit to two Ge2Se7 ditetrahedra. The inert pair of the SbIII atom is sterically active, as reflected in a severely irregular Se coordination reminiscent of the situation in Sb2Se3. The Ba4LaGe3SbSe13 is an electron-precise compound, according to the ionic formulation (Ba2+)4(La3+)(Ge4+)3Sb3+(Se2-)13, reflects itself in its red color. Assoud et al., also have calculated the electronic structure using linear muffin-tin method within the local density approximation (LDA) obtaining an energy gap of about 1.50 eV which disagree with the experimental one (2.0 eV) [33]. It is well-known that LDA scheme [32] usually underestimated the calculated energy gap within DFT in comparison to the experimental data. The LDA is the simplest format not adequately flexible to reproduce both the exchange–correlation energy and its charge derivative accurately which generally cause to underestimate the energy band gap [38]. To overcome this drawback Engel and Vosko [37] constructed a new functional form the generalized gradient approximation (GGA) which is able to better reproduce the exchange potential at the expense of less agreement in the exchange energy. This approach, called EV-GGA, yields better band splitting [39, 40]. Therefore we think it would be beneficial to use Engel-Vosko generalized gradient approximation (EVGGA) [37] which optimizes the corresponding potential for band-structure calculations for such calculation. The above discussion clarify that most of the previous work is focused on the structural properties of the investigated compound. In present work we concentrate on density of states, electronic charge density and thermoelectric properties, using full potential linear augmented plane wave (FLAPW), which is one of the most accurate method [34, 35]. |
II. CRYSTAL STRUCTURE AND COMPTATIONAL DETAIL |
| The crystal structure of Ba4LaGe3SbSe13 as shown in Fig.1, is stable in monoclinic symmetry with space group P21/c (no.14). |
| The crystallographic data of Ba4LaGe3SbSe13 which taken from Ref. 31, were optimized by minimizing the forces acting on each atom. We have used full potential linear augmented plane wave (FPLAPW) within the framework WIEN2K package [36]. The exchange correlation potential was solved by Engel-Vosko generalized gradient approximation (EVGGA) [37]. In order to converge the energy eigenvalues, the wave function in the interstitial regions were expended in plane waves with cutoff RMTKmax=7.0. Whereas RMT and Kmax symbolize the muffin-tin (MT) sphere radius and magnitude of largest K vector in plane wave expansion. The selected RMT is 1.24 atomic units (a.u.) for Ba, La, Ge, Sb and Se atoms. The wave function inside the MT sphere was expended up to lmax=10 while the Fourier expansion of the charge density was up to Gmax=12 (a.u)-1. The self-consistent calculations are believed to be converged when the difference in total energy of the crystal did not exceed 10-5Ryd for successive steps. The self consistent calculations were obtained by 84 k points in irreducible Brillouin zone (IBZ). |
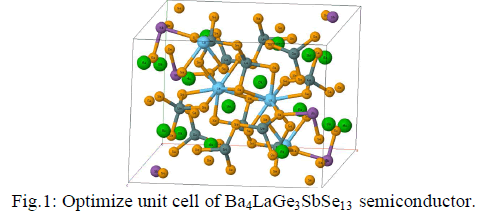 |
| The crystallographic data of Ba4LaGe3SbSe13 which taken from Ref. 31, were optimized by minimizing the forces acting on each atom. We have used full potential linear augmented plane wave (FPLAPW) within the framework WIEN2K package [36]. The exchange correlation potential was solved by Engel-Vosko generalized gradient approximation (EVGGA) [37]. In order to converge the energy eigenvalues, the wave function in the interstitial regions were expended in plane waves with cutoff RMTKmax=7.0. Whereas RMT and Kmax symbolize the muffin-tin (MT) sphere radius and magnitude of largest K vector in plane wave expansion. The selected RMT is 1.24 atomic units (a.u.) for Ba, La, Ge, Sb and Se atoms. The wave function inside the MT sphere was expended up to lmax=10 while the Fourier expansion of the charge density was up to Gmax=12 (a.u)-1. The self-consistent calculations are believed to be converged when the difference in total energy of the crystal did not exceed 10-5Ryd for successive steps. The self consistent calculations were obtained by 84 k points in irreducible Brillouin zone (IBZ). |
III. RESULTS AND DISCUSSION |
| Density of state The calculated total density of state (TDOS) along with partial density of state for Ba4LaGe3SbSe13 are shown in Fig.2a-e. The TDOS exhibit an energy band gap (Eg) of about 1.60 eV. From the calculated partial density of states as shown in Fig.2b-e, one can notice that the calculated core bands in energy range between -13.5 eV and -11.3 eV are originated mainly from dominant Ba-p state (8.6 states/eV) and Se-s state (2.5 states/eV), with small contribution of Ge-s/p/d, Sb-s/p and La-p states. From -8.5 eV to -7.5 eV, the formation of the bands occurs mainly from Ge-s (2.3 states/eV), Sb-s (1.3 states/eV) with minor contribution of La-p and Sed states. From -4.0 eV to Fermi level the bands are fashioned by prevailing Se-p state(1.3 states/eV), Ge-p state(0.45 states/eV), Sb-p state (0.35 states/eV) with insignificant contribution from La-p/d, Sb-s/p, Ge-p/d and Ba-d states. The upper valence band is shaped by combination of Se-p, Sb-s/p and La-p states while the conduction band is formed by Se-p/d, Sb-s/p/d and La-d states. Both Ge-s (0.40 states/eV) and Sb-p states (0.45 states/eV) show dominancy in conduction band formation. La-d state (1.05 states/eV) is foremost in energy range between 3.0 eV and 7.0 eV. The next dominant peaks in this region are Ba-d and Ge-p states with values of (0.85 states/eV) and (0.55 states/eV), respectively. The contribution of the rest states (Se-p/d, Ge-d) in this regin is small. The higher energy bands region (7.0 eV up to 14.6 eV) are formed by Ge-p/d, Se-p/d, Ba-s/d, La-s/p/d and Sb-s/p/d states. In this range Bad( 0.15 states/eV), La-d (0.14 states/eV), and Se-d (0.14 states/eV), are predominant while Sb-s, Ba-s and La-s show small contribution. |
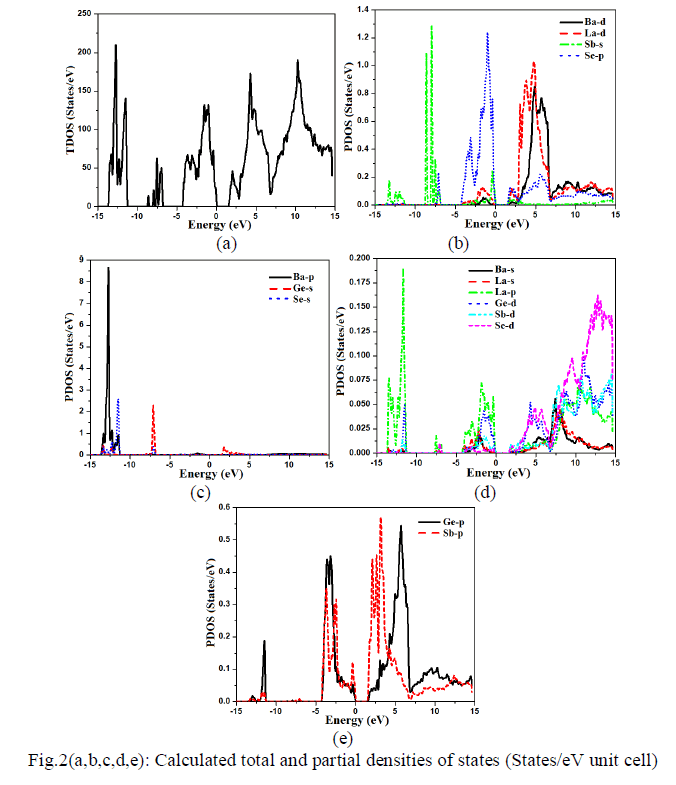 |
| Electronic charge density The electronic charge density contour plot is the best way for accurate explanation of bond nature [41, 42]. We have calculated the distribution of charge density in three different crystallographic planes for visualization of chemical bonding nature among the composition of Ba4LaGe3SbSe13 as shown in Fig.3a-c. The intensity of charge density is shown in thermo-scale of Fig.3 in which the red color shows the zero charge density while the blue color shows the maximum intensity. Fig.3 elucidates foremost covalent nature of bond with very small part of ionicity in Se‒Ge and Se‒Sb configuration while that of Se‒Ba and Se‒La show mixed ioniccovalent character of bonds. The bonding nature of the compound can also be calculated analytically in term of electro-negativities using the Pauling scale. The percentage ionicity of bonds in term of electro-negativity difference is calculated using an empirical relation given in ref. 43. The electro-negativity difference of Se‒Ge (0.6) and Se‒Sb (0.5) also verify dominant covalent bond with small percentage (10% and 8.9%) ionicity while Se‒Ba (1.7) and Se‒La (1.5) show mixed ionic-covalent bond. Both Se‒Ba and Se‒La show 37.3 % and 31.8% ionicity. The calculated bond lengths of Ba4LaGe3SbSe13, as listed in Table 1, show close agreement with experimental data [31]. |
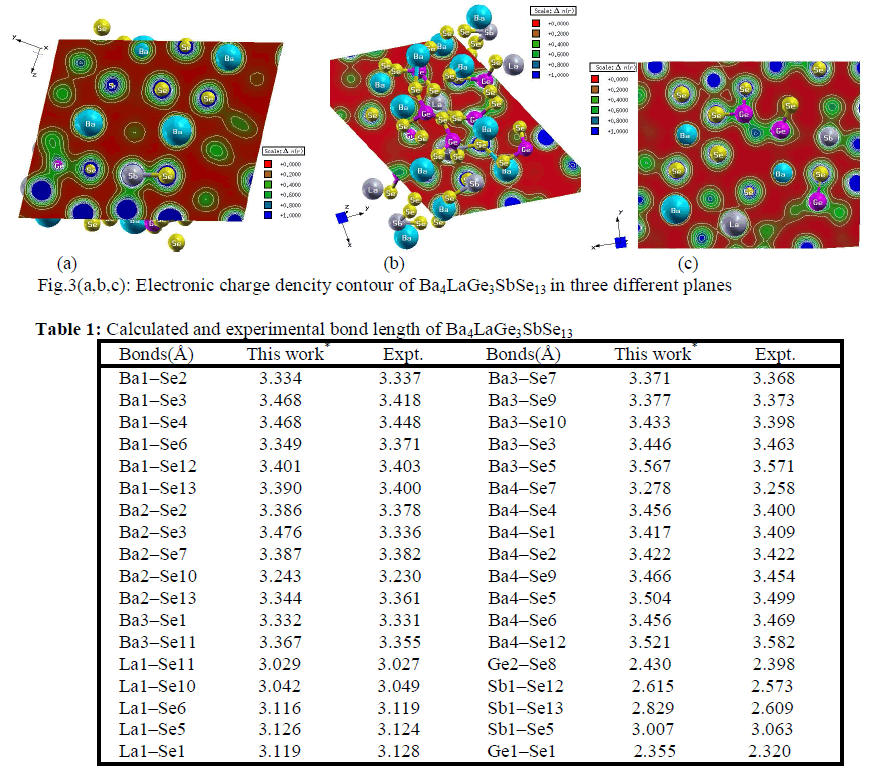 |
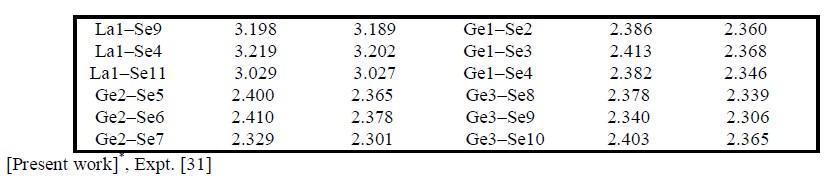 |
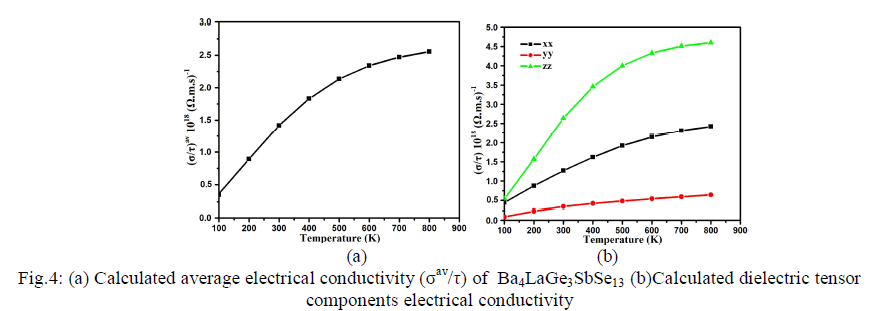
| Thermoelectric Properties Standard Boltzmann kinetic transport theory and the rigid band approach were used for calculating the thermoelectric transport properties based on band structure [44]. For evaluation of thermoelectric properties we evaluate the three basic quantities electrical conductivity , Seebeck coefficient S and thermal conductivity 0 k tensors which are functions of temperature (T) and chemical potential (μ) [44, 45]. We have used the BoltzTrap program [44] in order to calculate the transport properties of Ba4LaGe3SbSe13 which depend on a well tested smoothed Fourier interpolation to get an analytical expression of bands. In the BoltzTrap program there is no possibility to calculate electrons relaxation time (τ) from electronic band structure therefore 'τ' is assumed to be constant. It is also assumed that the electrons take part in the transport in narrow energy range due to the delta-function like Fermi broadening [45] The electrons relaxation time is constant for such a slender energy range. The correctness of this procedure has been checked previously and was exposed to be very good approximation [44, 46]. The dependence of temperature for energy band structure is disregarded. Moreover high electric conductivity, large Seebeck coefficient and low thermal conductivity are conformed to be responsible for high efficiency of thermoelectric materials [47]. The average value of electrical conductivity tensor components (σav/τ) of Ba4LaGe3SbSe13 is shown in Fig.4a. At 100 K the value of (σav/τ) is found to be 0.35×1018(Ω.m.s)-1. The average electrical conductivity linearly increase to 0.89×1018(Ω.m.s)- 1, 1.40×1018(Ω.m.s)-1, 1.75×1018(Ω.m.s)-1and 0.35×1018 (Ω.m.s)-1 for 200 K, 300 K, 400 K and 500 K, respectively. Further increase in temperature leads to decrease the ascending rate, as result the σav/τ curve going to be saturated at higher temperature to show its maximum value of about 2.50×1018 (Ω.m.s)-1 at 800 K. Since the investigated compound has orthorhombic symmetry therefore there exist three dominant tensor components on the diagonal of the matrix. Fig.4b represents the three second order dielectric tensor components of electrical conductivity σ/τ. There is considerable anisotropy among xx, yy and zz components of σ/τ. The zz component show dominancy and is more responsible for greater value of σ/τ. The yy component show negligible contribution while xx component play intermediate role between the two components (yy and zz). |
 |
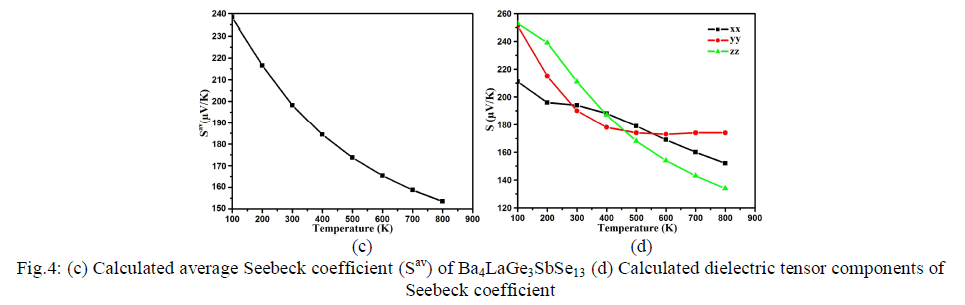
| The next major factor for calculation of thermoelectric transport properties is Seebeck coefficient which makes decision about the effectiveness of thermocouples. It is related to the fact that electrons communicate both charge and heat. The diffusion of the electron counts on temperature slope present in the material which conceives the opposite electric field and therefore voltage renowned as Seebeck voltage. The tendency of the spectra in the Seebeck coefficient and electronic conductivity depends on the Seebeck voltage. Its sign and magnitude are interrelated to an asymmetry distribution of electron round the Fermi grade [48]. The Fermi energy of the material is related to asymmetric energy distribution of electrons moving in the material which give greater value of Seebeck coefficient. Conversely decrease in the Joule heating consequences diminish in conductivity. Fig.4c shows the average value of Seebeck coefficient (Sav), the maximum value of about 238.0 μV/K at 100 K. When the temperature is increased to 200 K, there is abrupt decrease in Sav and then a further decrease to 197.0 μV/K, 185.0 μV/K, 173.0 μV/K, , 165.0 μV/K, 159.0 μV/K, and 197.0 μV/K, 154.5 μV/K, for 300 K, 400 K, 500 K, 600 K, 700 K and 800 K, respectively. From Fig.4d, one can also see the anisotropic behavior among the three components (xx, yy and zz) of S, which elucidates a considerable anisotropy for the whole range of temperature. |
 |
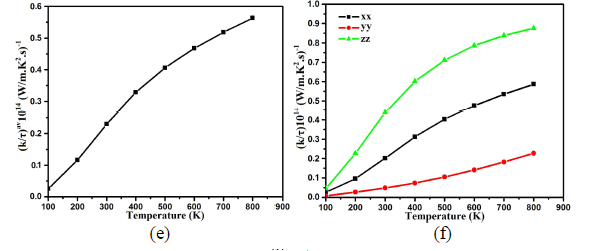
| Thermal conductivity is physical quantity of a material that conducts heat. It is approximated mainly in terms of Fourier's law of heat conduction. The over all tendencies of thermal conductivity spectra displays that transfer of heat take place as one move towards higher temperature which results linear increase in thermal conductivity depends on the nature of the material. Average thermal conductivity kav/τ of Ba4LaGe3SbSe13 is 0.030×1014W/mKs at 100 K as demonstrated in Fig.4e. The increasing rate in thermal conductivity is greater in the temperature range between 100 K and 400 K (0.325×1014W/mKs). For higher temperature the spectra become smooth and show its maximum value of 0.56×1014W/mKs at 800 K. Fig.4f show considerable anisotropy among the three components of dielectric tensor of thermal conductivity. The zz- component is dominant and play the leading role. |
 |
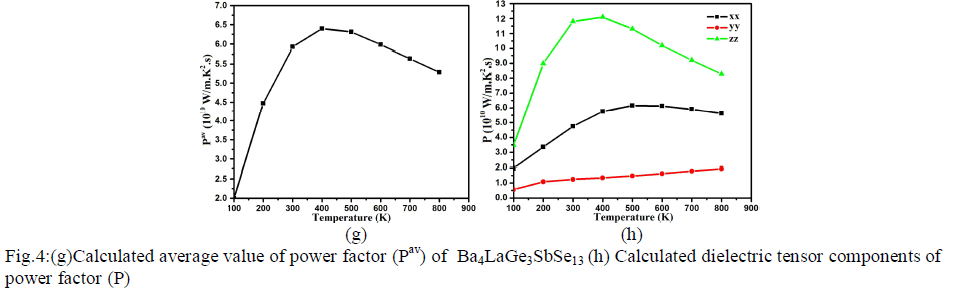
| Fig.4: (e) Calculated average thermal conductivity (σav/τ) of Ba4LaGe3SbSe13 (f) Calculated dielectric tensor components of Seebeck coefficient Power factor Power factor is also a momentous quantity for measuring transport properties. It is the net effect electrical conductivity and Seebeck coefficient. The calculated values of the power factor (Pav=S2σ/τ) for Ba4LaGe3SbSe13 is shown in Fig.4g. At 100 K the calculated value of power factor is 2.10×1010W/mK2s. There is major increase in Pav value at 200 K (4.48×1010W/mK2s) and 300 K (5.59×1010W/mK2s) which become more significant at 400 K and expose maximum value of 6.3×1010W/mK2s. At 500 K the Pav reduced to 6.27×1010W/mK2s. As one move to higher temperature (600 K, 700 K and 800 K) there is linear decrease in Pav spectra (5.90×1010W/mK2s, 5.60×1010W/mK2s and 5.25×1010W/mK2s). The three dominant dielectric components (xx, yy and zz) of the power factor show considerable anisotropy as shown in Fig.4h. |
 |
IV. CONCLUSION |
| We have calculated the total and partial density of state, electric charge density and transport properties of Ba4LaGe3SbSe13. In this calculation we have used full potential linear augmented plane wave (FPLAPW) as implemented in WIEN2k code within the framework of DFT. In order to solve exchange correlation potential we applied Engel Vosko generalized gradient approximation (EVGGA). The calculated total density of state clarified that Ba4LaGe3SbSe13 acquire small band gap (1.60 eV). The partial density of state were calculated and discussed in detail. The calculated electronic charge density contour plot confirmed the mixed ionic-covalent nature of the bond. The present simulations and analytical results exposed that both Se‒Ge and Se‒Sb show dominant covalent bond with small percentage ionicity whereas Se‒Ba and Se‒La results mixed ionic-covalent bond. The transport properties were calculated using the Boltzmann transport theory. The average value of tensor components of electrical conductivity, Seebeck coefficient, thermal conductivity and power factor were calculated discussed in detail in temperature range between 100 K and 800 K. The power factor of Ba4LaGe3SbSe13 exposed that it is prospective applicant for thermoelectric technological applications around 400 K. |
Acknowledgment |
| The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme. |
References |
|