ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Hilina Vadavathi, Teena Thankachan, Shabitha A., Pooja Rokade1 B.E. Students, Dept of Computer Engineering, Pimpri Chinchwad College of Engineering, Pune, Maharashtra, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Images proved to be better medium for sharing sensitive data. Earlier secret sharing schemes were based on numbers and further were also applied on images. Most of the existing schemes proposed do not have the capability of verification of the shares and hence are prone to cheating either by the original secret holder or the participants. Some of these schemes provided security but required additional computation in the form of certificate vectors or error correction codes The intent of this paper is to discuss the verifiable secret sharing schemes. The paper analyses these schemes and presents a comparative study of the same. The parameters used for comparative study are threshold, cheater identification, techniques used for verification, need secure channel, etc. This paper will support in choosing the verifiable secret sharing scheme for specific applications.
Keywords |
| Secret sharing; Information Security, Verifiable Secret Sharing, Cheating detection |
INTRODUCTION |
| With the advent of internet technology, data is being transmitted across the network at a very high speed every second. Secure transmission of sensitive data is of major concern. Cryptographic techniques have been widely used for the same. But these techniques have a major drawback i.e. there is a common key to decrypt the data. Loss or damage to key implies loss of data. To solve this problem secret sharing schemes have been introduced wherein the key is distributed amongst a group of people, and subset of this group can come together and reconstruct the secret. A secret sharing scheme is a method of distributing a secret amongst a set of participants by giving each participant a share in such a way that any subsets of participants can reconstruct the secret from a pooling of their shares. Secret sharing schemes are highly versatile cryptographic primitives and, as a result, have been employed in a vast range of different applications including protection of cryptographic keys, access control, key recovery mechanisms, electronic voting, distributed certificate authorities, online auctions and secure multiparty computation. Many secret sharing systems have been proposed so far, Shamir [1] and Blakely’s [6] scheme being the primitives. These primitive schemes gave the basic secret sharing scheme but had certain drawbacks. Further on, in many schemes verifiability was introduced as an extension to these schemes. Verifiable Secret Sharing In most of the secret sharing schemes it is assumed that the Dealer is reliable, however, if a dealer misbehaves and distributes inconsistent shares to the participants, then secret is not reconstructed. To prevent such malicious behavior of the dealer, one needs to implement a protocol through which a consistent distribution can be verified by the recipients of shares. The problem of verifiable secret sharing is to convince shareholders that their shares are t-Consistent. Of course if the shareholders would transfer their shares, they could easily confirm consistency, however this would contradict the purpose of the secret sharing scheme. Publically verifiable secret sharing: In this scheme the secret can be checked by the shareholder himself or by anybody, to be correct. Various schemes are introduced to verify and detect cheating which included use of Game Theory (to prevent rational participants cheating), A cheat- Proof Rational Secret Sharing scheme (extended form of Game Theory) Detecting Dealer Cheating and Resistance against cheating. |
II. TYPES OF ATTACKS OF CHEATERS |
| Since all these scheme are prone to cheating, following types of attacks by cheaters have been identified and proposed by one of these schemes. Type 1 attack: the cheaters of this type attack can be either honest shareholders who present their shares in error accidentally or dishonest shareholders who present their faked shares without any collaboration. Each faked share of this attack is just a random integer and is completely independent with other shares. Type 2 attack: the cheaters of this type attack are on purpose to fool honest shareholders. In this type attack, we assume that all shareholders release their shares synchronously. Thus, cheaters can only collaborate among themselves to figure out their faked shares before secret reconstruction; but cannot modify their shares after knowing honest shareholders’ shares (i.e. we assume that all shares must be revealed simultaneously). Under this assumption, only when the number of cheaters is larger than or equal to the threshold value t, the cheaters can implement an attack successfully to fool honest shareholders. Type 3 attack: the cheaters of this type attack are dishonest shareholders who modify their shares on purpose to fool honest shareholders. In this type attack, we assume that all shareholders release their shares asynchronously. Since shareholders release their shares one at a time, the optimum choice for cheaters is to release their shares after all honest shareholders releasing their shares. The cheaters can modify their shares accordingly. |
III. STUDY OF SOME EXISTING SCHEMES |
A. Shamir’s secret sharing scheme[1979] [1] |
| Shamir’s secret sharing scheme is a threshold scheme based on polynomial interpolation. It allows a dealer D to distribute a secret value s to n players, such that at least k < n players are required to reconstruct the secret. The protocol is information theoretically secure, i.e., any fewer than k participants cannot gain any information about the secret by themselves. This scheme is a very simple and efficient scheme to share a secret among n shareholders. However, when the shareholders present their shares in the secret reconstruction phase, dishonest shareholder(s) (i.e. cheater(s)) can exclusively derive the secret by presenting fake shares and thus the other share holders get nothing but a faked secret. This scheme does not prevent any malicious behavior of dishonest shareholders during secret reconstruction. |
B. Thein and Lin’s Scheme for secret sharing [2002] [2] |
| This scheme is an extension to Shamir’s scheme using images that proposed a method to generate shadows of smaller size. This paper proposes (k, n) secret image sharing method where the secret image is shared by n shadow images and any k shadow images (k≤ n) can be used to restore the whole secret image. The size of each shadow image is less (i.e. 1/k) than the original secret image. Even though this was a major contribution towards image secret sharing, this scheme too is not cheater proof. |
C. Detection And Identification of cheaters in (k, n) secret sharing scheme[2009] [3] |
| This Scheme is based on Shamir’s (k, n)-SS scheme. One unique feature of this scheme is that the same share is used for secret reconstruction to detect and identify cheaters. This scheme is an extension of Shamir’s (k, n)-SS scheme. In this scheme they consider the situation that there are more than t shareholders participated in the secret reconstruction. Since there are more than t shares (i.e. it only requires t shares) for reconstructing the secret, the redundant shares can be used for cheater detection and identification. This scheme uses the shares generated by the dealer to reconstruct the secret and, at the same time, to detect and identify cheater(s). This scheme too requires a secured channel. This paper discussed different types of attacks by cheaters. |
D. Cheating Resistance for Secret Sharing [2009] [4] |
| In this paper a notion, the (k, n)-threshold agreement certificate is proposed. The (k, n)-threshold agreement certificates of a secret are also shadows derived from the original secret using a different access structure. Based on these certificates, this paper presents a (k n)-threshold secret sharing scheme which can resist participants’ cheating. That is, any participant’s cheating would not work in the proposed scheme provided that the assumptions in the paper are true. |
| This papers proposes a scheme that uses an off-line TTP, a digital signature scheme, and an (n + 1; 2n – k + 1)-threshold secret sharing scheme to construct the notion, (k, n)-threshold agreement certificates. Hence, the computational complexity is more since there is an addition of generation of agreement certificates. Also the cheaters are detected but not the identified. |
E. A verifiable secret sharing scheme for binary images using watermarking [2011] [5] |
| Most verifiable secret sharing schemes allow their participants to verify only their received shadows instead of reconstructed secret image. If we verify the shadows after reconstruction it will be a better approach. For this kind verifiability watermarking is used. By combining low complexity visual cryptography along with the watermarking achieves both reliability and security. In Watermarking an image pattern is used for authentication of the image. A watermark image is merged or combined in the original image and is then sent through the network. When the receiver receives the image he checks for a watermark image first. If the original watermark image and reconstructed watermark image are same, then the original secret image is reconstructed successfully. This scheme uses a watermark image to verify the reconstructed secret image so that a defined participant does not need to execute shadow verification during both the shares reconstruction phase and the revealing phase. |
F. A new image secret sharing scheme to identify cheaters[2009] [6] |
| A verifiable image secret sharing scheme based on the Thien-Lin scheme and the intractability of the discrete logarithm. It solves the cheating problem in the Thien-Lin scheme; because the participant chooses her/his own secret shadow, no secret communication exists between the holder and the participants, so the new scheme doesn’t need a secure channel. This scheme was much better than the previous scheme. This was another great contribution. But this paper was again based on gray images. It did provide capability of cheater identification too but again need improvement against active attacks. |
IV. COMPARATIVE STUDY |
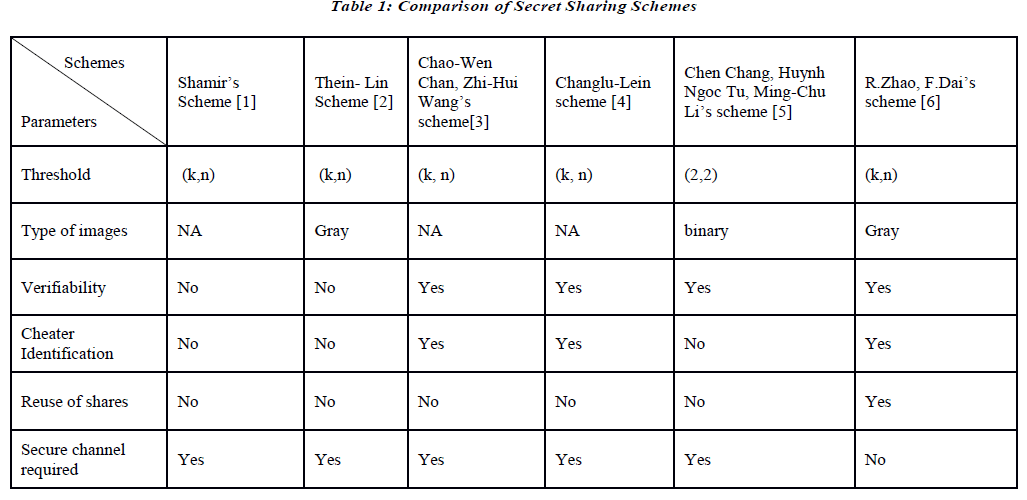
| The schemes discussed in the previous section are compared on the parameters like need of secure channel, cheater identification, techniques used for verification, etc. in below table 1. |
 |
 |
| The above table shows the comparative study of different verifiable secret sharing schemes. The comparative study shows that the schemes are not providing all the features as per the need of the application. It can be observed from the above table that the R.Zhao and F.Dai’s scheme [6], omits the need of secure channel in network. |
V. CONCLUSION |
| The intent of this paper is to discuss the verifiable secret sharing schemes. The paper analyses these schemes and presents a comparative study of the same. The comparative study helps in choosing the appropriate scheme for specific application. Unfortunately even these secret sharing schemes are prone to cheating by dishonest participants. So we require a more robust verifiable secret sharing system that will be cheater proof and provide better security. Also there is need for a verifiable secret sharing technique that can be applied on color images. |
References |
|