International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Enhanced GenMax Algorithm for Data Mining

Saifullahi Aminu Bello1, Abubakar Ado2, Tong Yujun3, Abubakar Sulaiman Gezawa4, Abduarra’uf Garba5
  1. Lecturer, Department of Computer science, Kano University of Science and Technolgy, Kano, Nigeria
  2. Lecturer, Department of Computer Science, Northwest University, Kano, Nigeria
  3. Professor, Electrical/Electronics, Liaoning University of Technology, Jinzhou, Liaoning Province, China
  4. System Analyst, MIS Department, Bayero University Kano, Kano, Nigeria
  5. Lecturer, Department of Computer Science, Northwest University, Kano, Nigeria
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Association rules mining is an important branch of data mining. Most of association rules mining algorithms make use of only one minimum support to mine items, which may be of different nature. Due to the difference in nature of items, some items may appear less frequent and yet they are very important, and setting a high minimum support may neglect those items. And setting a lower minimum support may result in combinatorial explosion. This result in what is termed as “rare item problem”. To address that, many algorithm where developed based on multiple minimum item support, where each item will have its minimum support. In this research paper, a faster algorithm is designed and analyzed and compared to the widely known enhanced Apriori algorithm. An experiment has been conducted and the results showed that the new algorithm can mine out not only the association rules to meet the demands of multiple minimum supports and but also mine out the rare but potentially profitable items’ association rules, and is also proved to be faster than the conventional enhanced Apriori

Keywords
Data Mining, Association Rules, Multiple Minimum Item supports, Apriori, GenMax Algorithm.

INTRODUCTION
Due to the ease at which data is saved and availability of memory spaces, data is growing exponentially. Data mining can extract the unknown but potentially useful information [1] from a mass, incomplete and noisy raw data. The Barcode technology use in the supermarkets allows easy recording of sale transactions. Data mining technologies in the sales centers/e-commerce have entered a practical stage and achieved good effects. In data mining, association rule learning is a popular and well researched method for discovering interesting relations between variables in large databases. It is intended to identify strong rules discovered in databases using different measures of interestingness. Association rules are usually required to satisfy a user-specified minimum support and a user-specified minimum confidence at the same time.
image
Usually one user specified minimum support is used when mining itemsets, any itemset whose proportion is greater than or equals the minimum item support is considered to be frequent. Due to the different nature of the items in a data set, some items are more frequent than the others, if a single minimum support is applied, the less frequent items cannot be mined except if the support is very low, and in that case the more frequent items will associates with all items in any possible way. Multiple Minimum Item Support (MMIS): the concept of multiple minimum item support is introduced to address the rare items problem.
2.4.2 CONFIDENCE: Confidence of a rule is the conditional probability of Y given X. Using probability notation: confidence (X implies Y) = P (Y given X).
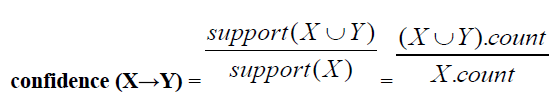image
This paper analyses the practical application of data mining on an e-commerce data to find the association rules between items. An algorithm use in [2] called GenMax algorithm which was used to mine out association rules between items based on single Minimum Item Supports is enhanced, thus allowing it to mine items based on multiple minimum item support as devised in [3], which is an enhancement of the conventional apriori algorithm.

RELATED WORK
2.1 ENHANCED APRIORI
Tong Yujun [3] analyzed an algorithm based on the original apriori algorithm according to a multiple user specified Minimum Item supports and support difference constraint.
Input: transaction T, MIS, φ
Output: frequent k-itemsets
Line 1 M=sort (I, MIS);
image
In the improved algorithm, the key operation is to sort the items of I in ascending order basing on their minimum item support values as is used in following operations (line 1), all the 1-itemset can be obtained in F1(line 2,3), function candidate-generate-level2(L, φ) can let the Down Closure Property principle be valid as usual(line 5), function candidate-generate (Fk-1, φ) (line 6) is similar to that in the Apriori algorithm but different in pruning step, and counting c-{c[1]} is to calculate the confidence of association rules (line 10). At last, the algorithm returns the union of frequent itemsets from 1-itemsets to k-itemsets (line 15).
2.2 GENMAX ALGORITHM
GenMax [2] is a backtrack search based algorithm for mining maximal frequent itemsets. GenMax uses a number of optimizations to quickly prune away a large portion of the subset search space. It uses a novel progressive focusing technique to eliminate non-maximal itemsets, and uses diffset propagation for fast frequency checking.
//Invocation: MFI-bactrack(Ø, F1, 0)
MFI-backtrack(Il, Cl, l)
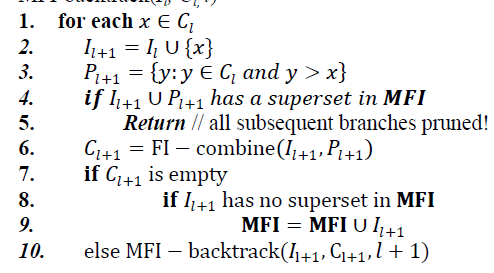image

FAST ALGORITHM WITH MMIS
The algorithm is an application of the idea developed in [3], the enhanced apriori with the one in [2], the genMax algorithm. Support difference constraint (SDC)[2]. In the improved algorithm the Down Closure Property principle is not satisfied. So after sorting the itemsets by their values of the MIS, SDC is introduced to generate frequent itemsets from the itemsets with the frequent, rare but potentially profitable ones. Suppose sup(i) is the real support of an item in itemsets, to each itemset the SDC is defined as
image
The algorithm is best described following the solution in section 4.2

EXPERIMENT AND ANALYSIS
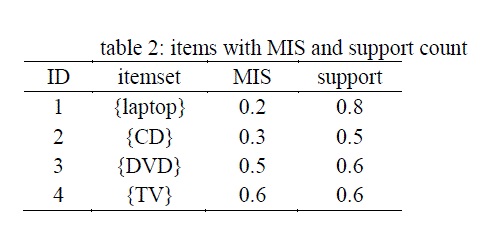
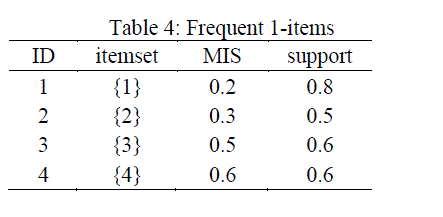
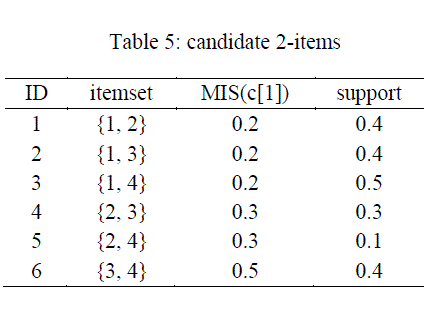
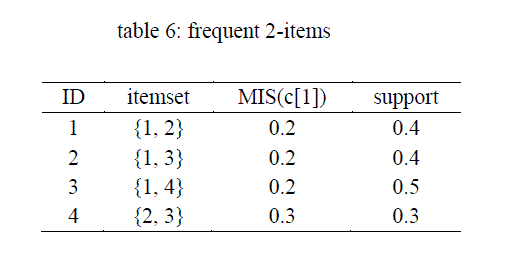
the experiment make use of an e-cart data obtained some times in May, 2013 from an e-commerce website as shown in table 1. Table 1 shows the transactions obtained. And table 2 indicates the items with there respective minimum support and there count in the transaction shown is a sorted ascending order of their minimum support.
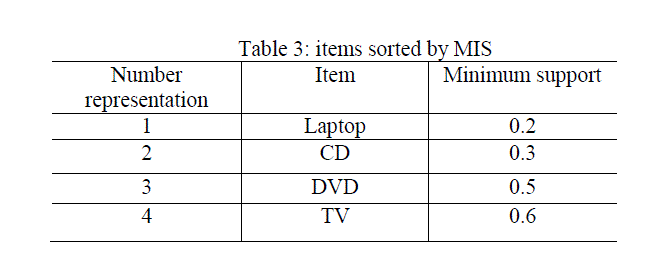
image
image
For easy sorting of the items, the items are represented by numbers, 1, 2, 3, 4 according to there minimum supports.
image
4.1 USING ALGORITHM FROM SECTION 2.1
Following the algorithm proposed in 3. The above transactions is mined in this way
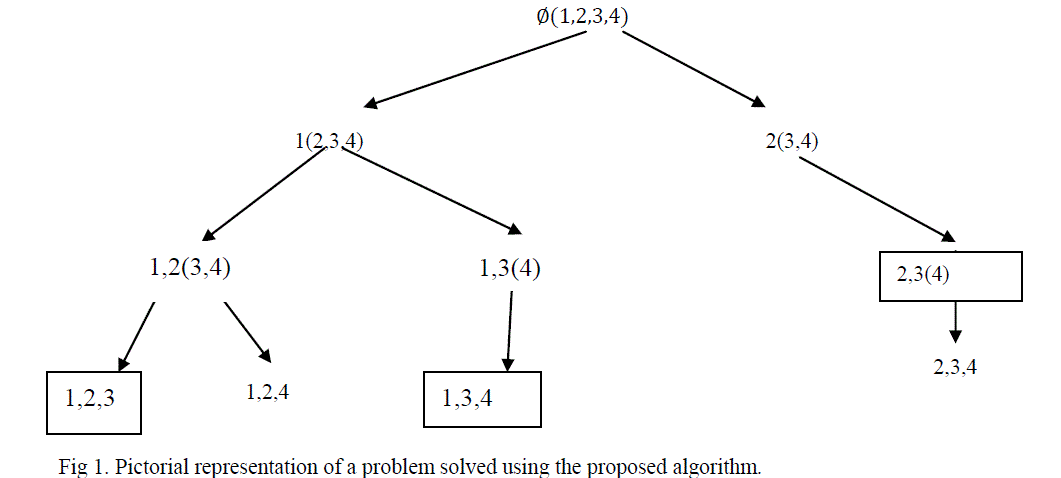image
image
image
image
Items in the box represent the maximal frequent items sets.
Thus, the maximal frequent item sets are [{2,3}, {1,2,3}, {1,3,4}]
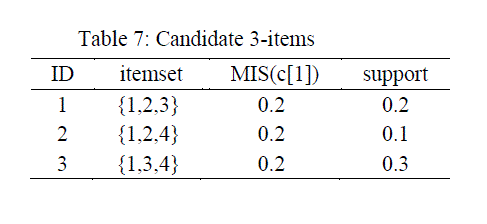
The two frequent 3-items sets corresponds to those obtained from 3.1 above.
To find the remaining frequent item sets, we first find all the possible subsets of the above maximal frequent item-sets.
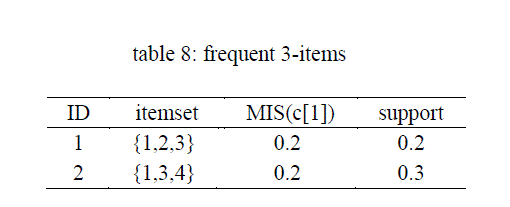image
image
From the above subsets, in table 9, only one subset is, {3,4} not frequent.

4.3 COMPARISON OF 3.1 AND 3.2
Under the approach in [3], the 2-item candidate set is the largest candidate set. This is always the case both in [1] and [3]. From the above examples, it is evident to see that the number of candidate sets generated to find the maximal frequent item sets is much lower than the number of candidates generated directly to find all the frequent item sets. And while both approaches arrives at the same frequent item sets, the number of candidate sets in the proposed algorithm is lower than the approach used in [3]. Based on this advantage and the fact that the algorithm in [3] follows the principle: the (n-1) frequent itemsets is used to generate n-frequent candidate sets, the number of transaction traversing in [3] is greater than the number of traversing is the proposed algorithm. Below is a graph that shows the above advantages more clearly:
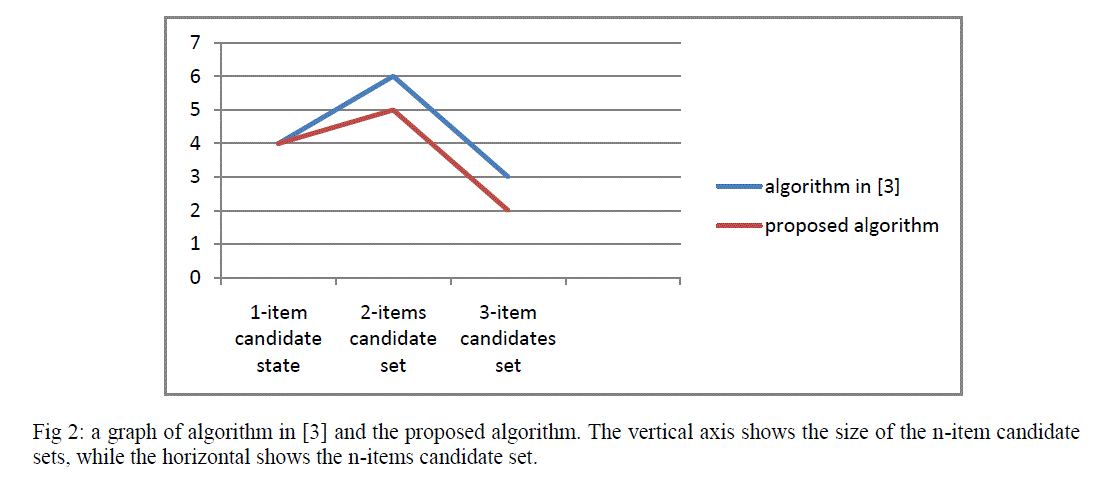image
Fig 2: a graph of algorithm in [3] and the proposed algorithm. The vertical axis shows the size of the n-item candidate sets, while the horizontal shows the n-items candidate set.

CONCLUSION
While due to the nature of items in real life, using a single minimum item support results in rare items problem. The issue is addressed with multiple minimum item supports as proposed in [3]. The algorithm proposed in this paper uses the same technique of multiple minimum item support but is proved to be more efficient than the algorithm in [3] which is an enhancement of the conventional apriori algorithm. The proposed algorithm reduced the number of candidate item sets, thus reduced the number of transaction traversing which in effect will reduce the programming timing and the memory cost. Since the algorithm find directly the maximal frequent itemsets, it can be used where only the maximal frequent item sets is required. Maximal frequent item sets are used in several data mining tasks such as incremental mining of dynamic databases.

References
  1. R. Agrawal, and R. Srikant. Fast algorithms for mining association rules in large database. Technical Report FJ9839, IBM Almaden Research Center , San Jose, CA,(Jun. 1994),p.2-6
  2. Matthew Eric, Oteyy Adriano, Velosoyz Chao, Wangy Srinivasan, Parthasarathyy Wagner, Meira Jr.z, ”Incremental Techniques for Mining Dynamic and Distributed Databases” Computer and Information Science Department The Ohio-State University. (n.d.)
  3. Yujun Tong, Jun Zhou, Wen’ge Xie, Dan Jia, “Research and Application of an Enhanced Data Mining Algorithm”.ICMM2011, 841-844. 2011,Jinzhou, China.
  4. J, Han and Y. Fu. Discovery of multiple-level association rules from large databases. In Proc. 1995 Int. Conf. Very Large Databases(VLDB’95)( Sep. 1995), p.402-431.
  5. Shilpa, Sunita Parashar, “Performance Analysis of Apriori Algorithm with Progressive Approach for Mining Data” International Journal of Computer Applications (0975 – 8887) Volume 31– No.1, October 2011.
  6. Karam Gouda, Mohammed J. Zaki, “GenMax: An Efficient Algorithm for Mining Maximal Frequent Itemsets” Data Mining and Knowledge Discovery, 11, 1–20, 2005
  7. Bing L, Wynne H , Yiming M. Mining Association Rules with Multiple Minimum Supports. In: KDD-99.San Diego,USA(1999).
  8. D. Cheung, J. Han, V. Ng, and C. Wong. Maintenance of discovered association rules in large databases: An incremental update technique. In Proc. of the 12th Int. Conf. on Data Engineering (ICDE’96), March 1996.
  9. J, Han and Y. Fu. Discovery of multiple-level association rules from large databases. In Proc. 1995 Int. Conf. Very Large Databases(VLDB’95)( Sep. 1995), p.402-431.
  10. R. Agrawal, et al. Mining association rules between sets of items in large databases. Proceedings of the ACM SIGMOD Conference on Management of data(May 1993), p. 207-216.
  11. SIGMOD-98, 1998. [11] Park, J. S. Chen, M. S. and Yu, P. S. “An effective hash based algorithm for mining association rules.” SIGMOD-95, 1995, pp. 175-186.
  12. Rastogi, R. and Shim, K. “Mining optimized association rules with categorical and numeric attributes.” ICDE –98.
  13. Liu, B., Hsu, W. and Ma, Y. Mining association rules with multiple minimum supports. SoC technical report, 1999.
  14. Piatetsky-Shapiro, Gregory (1991), Discovery, analysis, and presentation of strong rules, in Piatetsky-Shapiro, Gregory; and Frawley, William J.; eds., Knowledge Discovery in Databases, AAAI/MIT Press, Cambridge, MA.
  15. Salleb-Aouissi, Ansaf; Vrain, Christel; and Nortet, Cyril (2007). "QuantMiner: A Genetic Algorithm for Mining Quantitative Association Rules". International Joint Conference on Artificial Intelligence (IJCAI): 1035–1040.
  16. Bayardo, Roberto J., Jr.; Agrawal, Rakesh; Gunopulos, Dimitrios (2000). "Constraint-based rule mining in large, dense databases". Data Mining and Knowledge Discovery 4 (2): 217–240.doi:10.1023/A:1009895914772
  17. Rauch, Jan; Logical calculi for knowledge discovery in databases, in Proceedings of the First European Symposium on Principles of Data Mining and Knowledge Discovery, Springer, 1997, pp. 47-57
  18. Bayardo Jr, Roberto J. "Efficiently mining long patterns from databases." ACM Sigmod Record. Vol. 27. No. 2. ACM, 1998.