International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Estimating the Economic Quantities of Different Concrete Slab Types

Dr.AmrAbohashish1 and Dr.Ahmed M. Ebid2
  1. Assistant Prof., Civil Eng. Dpt., Mataria, Helwan Uni., Cairo, Egypt
  2. Lecturer, Str. Dpt., Faculty of Eng. & Tech., Future Uni., Cairo, Egypt
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The economy of the structural design of reinforced concrete buildings is usually evaluated by comparing the concrete volume per unit area and rebar weight per unit volume with certain empirical values depending on the type of the structure and the past experience of the judging engineer. The aim of this paper is to refine those empirical values and give that past experience the required scientific base. In order to achieve that goal, simplified methods of design that stated in most of reinforced concrete design codes are used to figure out the required quantities of concrete and reinforcement steel for different structural elements and types. Some reasonable assumptions are used to facilitate the mathematical formulas to be usable and presentable. Produced formulas are accurate enough to be used in rough estimation of concrete and rebar quantities, check quantity surveying results and evaluate the economy of the structural design.

Keywords
optimum quantities, rebar percentage, concrete slabs, cost estimation, quantity surveying.

ABBREVIATIONS
Image

INTRODUCTION
RC Slab is a horizontal concrete plate carries loads perpendicular to its plane. It transfers those loads to its supports either beams or columns. This load transfer generates mainly bending moments and shear stresses in the slab. Usually, some empirical values are used as optimum rebar percentage to evaluate the economy of certain design. Some of the most widely accepted values are (60-80 kg/m3) for solid slab and (120-140 kg/m3) of flat slabs.
This paper aims to evaluate the optimum thickness and rebar percentage of solid, hollow block, flat slab and waffle slab based on the simplified design methods stated in most reinforced concrete design codes.
Normally, design and quantities will be affected by several variables such as loads, spans, boundary conditions, used martials, rebar detailing, ..etc., hence, in order to facilitate the study, the following assumptions are considered:
Slab loads: Consists of its own weight, superimposed loads and live loads. Own weigh is well defined and it is equal to slab thickness times the reinforced concrete density, while the superimposed loads and live loads are widely varied according to type of finishing and the room activity, also there might be partitions loads directly on the slabs. Generally, large slabs are more likely to either be public area or have partition loads than small slabs. Hence, it is expected that slab load proportionally increases with slab area. Superimposed load is ranged between (0.15 – 0.25) t/m2, live load is ranged between (0.2 – 0.6) t/m2, and partition load is ranged between (0.0 – 0.4) t/m2 [2],[3]. It should be noted that the increase of loads is either due to live load or partition load not both of them. Assuming that the short span of the slab is ranged between 4.0 to 10.0 m, then smallest slab should has smallest loads and via versa. Hence, the summation of superimposed load, live load and partition load for 4.0m span is (0.15+0.2+0.0=0.35 t/m2) and for 10.0m span is (0.25+0.2+0.4=0.85 t/m2). So, the load/span ratio is ranged between (0.88 - 0.85) t/m2/m. Based on this study, slab loads except its own weight is about 0.90 t/m2 times its governing span in meters.
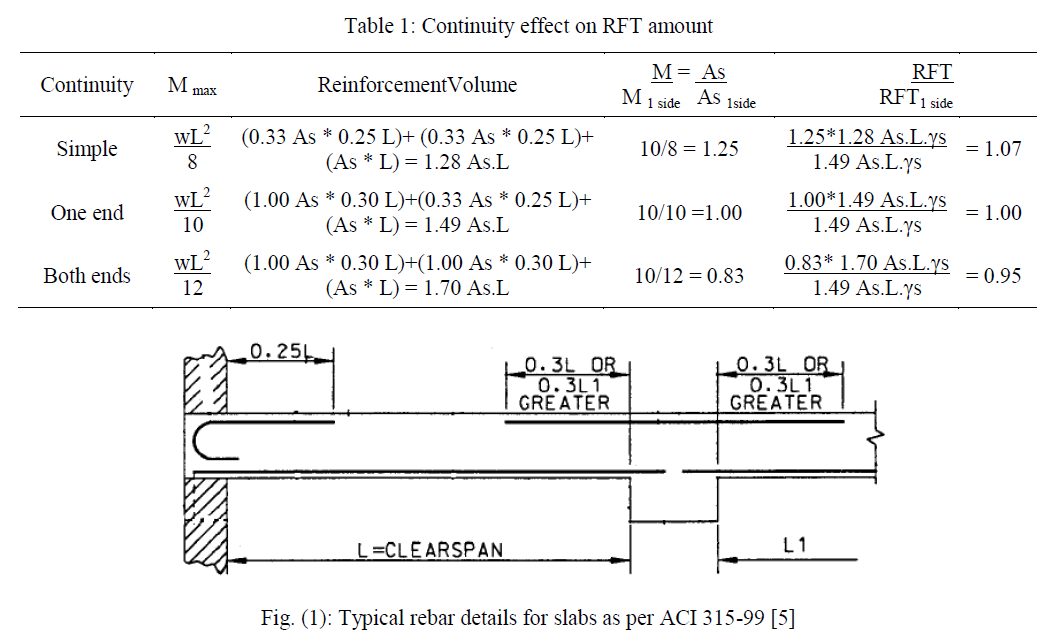
Continuity: Connections between considered bending element and adjacent elements have a major effect on bending moment distribution along this element. As per many codes, maximum bending moment for a simply supported element, one end and both ends continues element subjected to uniformly distributed load are (wL2/8), (wL2/10) and (wL2/12) respectively [1],[4]. Hence, the required reinforcement area for simply supported and both ends continues spans are 1.25 & 0.83 times the required reinforcement area for the one end continues identical span respectively. Also, the continuity of the element affects the detailing of the longitudinal reinforcement. Figure (1) shows the typical detail of solid slabs in ACI-315. Based on this detail the total volume of longitudinal reinforcement are (1.28 As.L), (1.49 As.L) & (1.70 As.L) for the simply supported, one end continues & both ends continues spans respectively, where (As) is the required area of reinforcement steel for each case. Table (1) shows the ratios between reinforcement weight in the three continuity cases and the one end continues case. The ratios are (1.07, 1.00 and 0.95) for the simply supported, one end continues & both ends continues spans respectively. Based on this analysis, all farther analysis will consider the one end continuity with error less than 7%
Image

SOLID SLABS
Solid slab is the basic type of slabs. It is defined as uniform thickness horizontal concrete plate supported by rigid beams on the edges. Rectangle solid slab is the most common shape, it has four edges, and each edge could be fixed, simply supported or free. According to ACI-318, minimum solid slab thickness meeting deflection requirement could be calculated as follows:
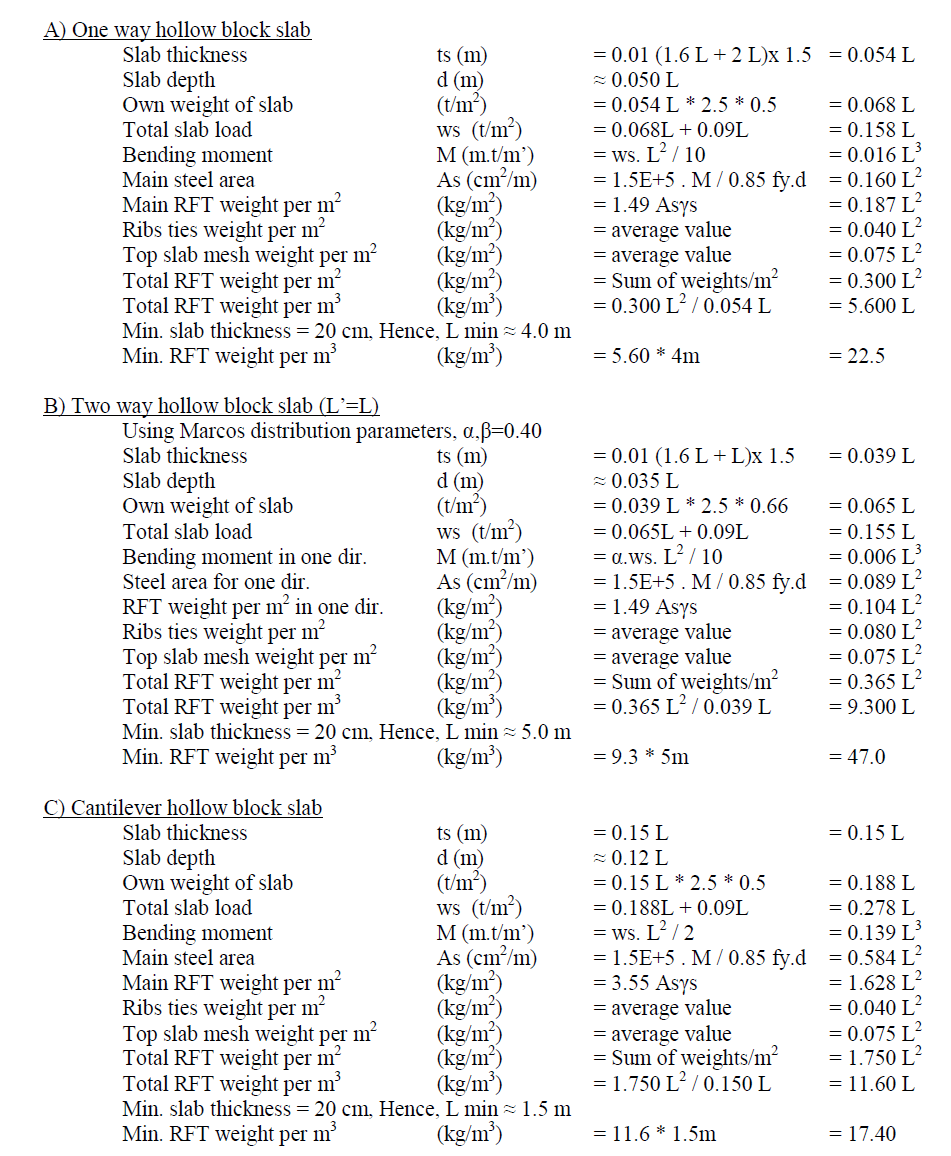
Image
Image

HOLLOW BLOCK SLABS
Hollow block slab is a ribbed slab formed using blocks of a material lighter than concrete, usually hollow clay blocks or foam blocks. Due to the limitation of the block size, the spacing between ribs is limited by 0.6m (0.5m is commonly used) and the minimum total depth of slab is limited by 20cm. Hollow block slab could be either one way or two ways. Due to the leakage if torsional rigidity and corner effect, Marcos parameters are used to distribute the load in the two ways slabs (α+β=0.80). It is a common practice to evaluate the rebar weight ratio relative to the total thickness of slab. All previous assumptions for solid slab thickness, load and continuity are still valid in case of hollow block slabs in addition to the following assumptions:
• Total slab thickness ≈ 1.5 slab thickness of equivalent solid slab
• Own weight of one way H.B. slab ≈ 0.5 own weight of equivalent solid slab
• Own weight of two ways H.B. slab ≈ 0.66 own weight of equivalent solid slab
• Own weight of cantilever H.B. slab ≈ 0.5 own weight of equivalent solid slab
• Rib spacing is about 0.5m.
• Span is ranged between 5 to 10 m.
• Rib ties are ranged between φ6-300 to φ8-200, average weight/m2 is 0.040 L2
• Top slab mesh is ranged between φ6-200 to φ10-200, average weight/m2 is 0.075 L2
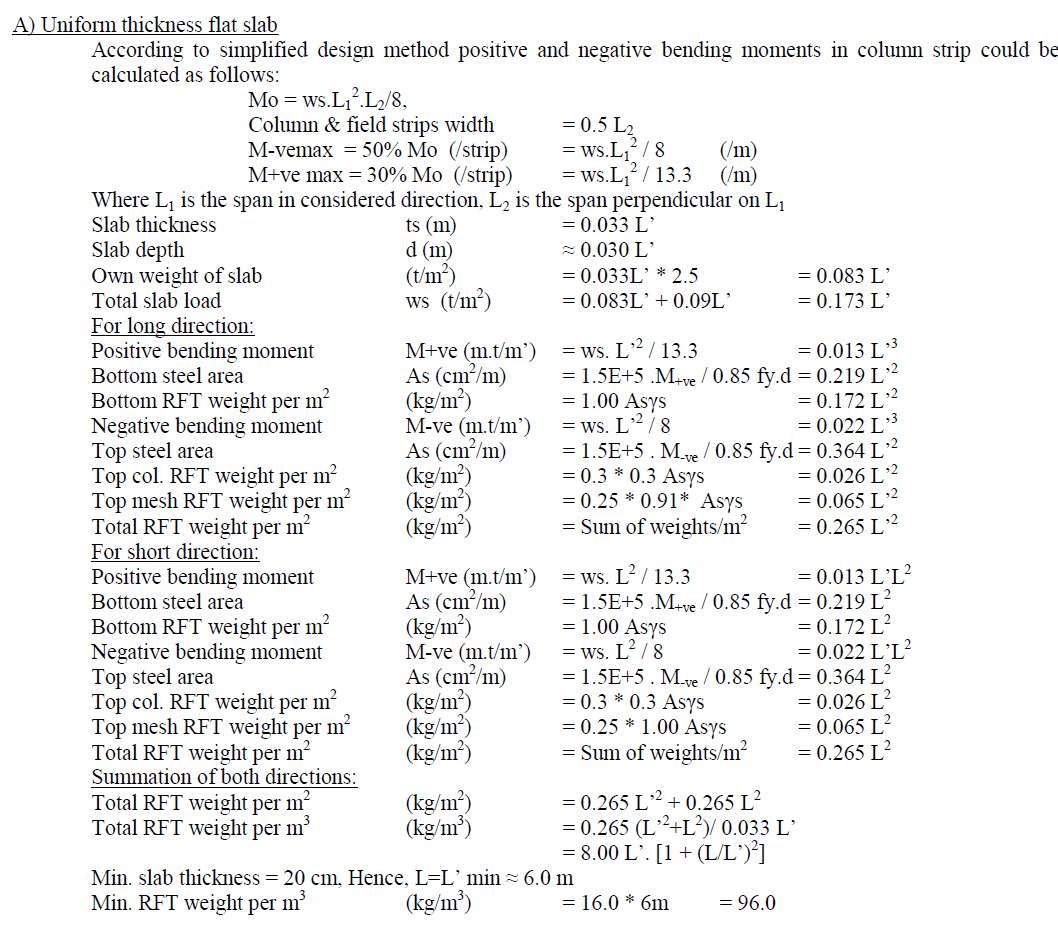
Image

FLAT SLABS
Flat slab is defined as the slab that is supported directly on the columns. It could have uniform thickness (flat plate) or variable thickness (flat slab with dropped panels). Also it could be solid or ribbed (Waffle slab). For uniformly loaded equal spans flat slabs, a simplified design method is stated in most codes depends on calculating the total bending moment in the span and distribute it in both positive and negative in field and column strips according to certain ratios depending of the uniformity of slab thickness and the stiffness of marginal beam.
The considered reinforcement detail is bottom mesh designed for the maximum positive bending moment, top reinforcement above columns designed for the maximum negative moment and extends one sixth the span in both directions and top mesh with area equals to 25% of the top reinforcement above columns (seismic requirement).Unlike the four sides supported slabs, flat & waffle slabs thickness is dominated by the long direction span (L’). Hence, it is better to represent the reinforcement weight per cubic meter as a function of (L’) instead of (L) for flat and waffle slabs.
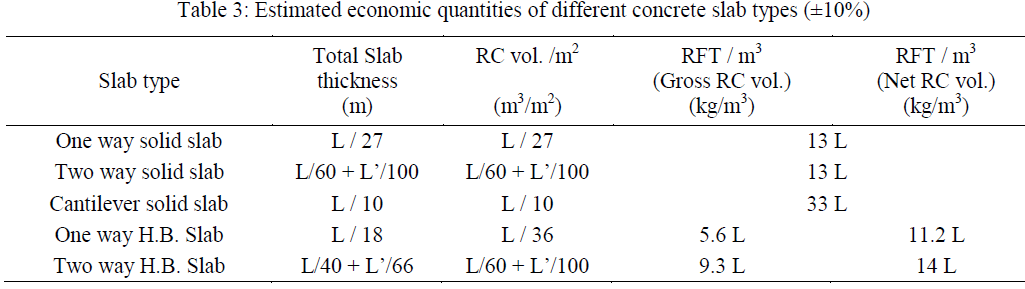
Image
Image
Image

CONCLUSION
Results of this study could be summarized in the following table:
Image
Image
Where: L & L’ are short & Long span of the slab respectively
Values in the table (3) are valid under the following conditions:
- Residential & office building (live load up to 300 kg/m2)
- Spans between 4.0 to 12.0 m
- High strength steel ( Fy = 3600 to 4000 kg/cm2)
- Characteristic concrete strength (Fcu = 250 to 350 kg/cm2)

References
  1. BS-6399-1-1996, “Loading for buildings-Part 1: Code of practice for dead and imposed loads”, © BSI, ISBN 0-580-26239-1
  2. SEI/ASCE-7-2005, “Minimum Design Loads for buildings and other Structures”, © (ASCE), ISBN 0-7844-0831-9
  3. BS-8110-1-1997, “Structural use of concrete-Part 1: Code of practice for design and construction”, © BSI, ISBN 0-580-26208-1
  4. ACI-318-2005, “Building Code Requirements for Structural Concrete”, © (ACI), ISBN 978-0-87031-745-3.
  5. ACI-315-1999, “Manual of standard practice for detailing reinforced concrete structures”, © (ACI).
  6. BS-CP-110-1987,” Code Of Practice For The Structural Use Of Concrete, Design, materials and workmanship”,© BSI, ISBN 0-580-07488-9
  7. David A. Fanella and S. K. Ghosh, “Simplified Design Reinforced Concrete Buildings of Moderate Size and Height”, © (PCA), ISBN 0- 89312-129-0.
  8. R. S. Narayanan & A. Beeby.“Designers' Guide To En 1992-1-1and En 1992-1-2, Eurocode 2: Design Of Concrete Structures General Rules And Rules For Buildings And Structural Fire Design”, © The authors and Thomas Telford Limited 2005, ISBN: 07277 3105 X
  9. C. H.Goodchild, “Economic Concrete Frame Elements“,© British Cement Association 1997, ISBN 0-7210-1488-7