ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Akshay Basavaraj B.Tech. Graduate, Department of Aerospace, Amrita School of Engineering, Coimbatore, Tamil Nadu, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Approximation of Drag Divergence Mach number, Critical Mach Number and the Coefficient of Wave Drag of non-transonic airfoils using Korn equation are presented in this research paper. Due to the presence of the CFD factor which influences the aforementioned parameters heavily, transonic airfoils develop an undue advantage over non-transonic airfoils. A preliminary analysis of the behaviour of the airfoils is done using XFLR5 wherein the aerodynamic characteristics such as coefficient of lift, coefficient of drag, pitching moment, stall angle and aerodynamic efficiency of the airfoils are evaluated at low Reynolds Number. In order to observe the effect of camber and thickness on the performance of airfoils, airfoils of varying camber and thickness are chosen. The airfoils chosen for this research paper are NACA 0012, NACA 0018, MH 23, NLF 0115, FX 83 W108, FX 66 S196, UltraSport 1000 and Clark Y (smooth). The main objective of this paper is to computationally obtain an airfoil which can perform well under both transonic and low Reynolds number conditions.
Keywords |
| Drag Divergence Mach Number, Critical Mach Number, Coefficient of Wave Drag, Non-transonic airfoils, CFD factor, XFLR5 |
INTRODUCTION |
| Airfoil selection plays a crucial role in determining the performance of an aircraft. It is essential in determining the cruise velocity, take-off and landing distances, turn rate, endurance, range and other factors which end up determining the overall efficiency of the aircraft[1]. Airfoils also have profound applications in missiles, gliders, vertical and horizontal axis wind turbines and cooling fans[2]. The generation of two major forces namely lift and drag constitute the performance of the airfoils and their applications. |
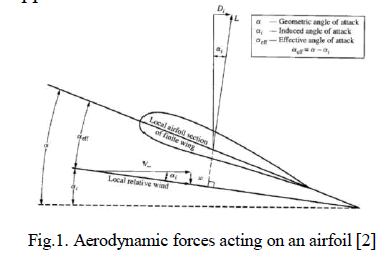 |
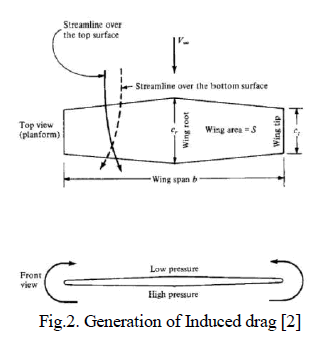
| For low Reynolds number applications such as gliders, sail planes, lift-based vertical axis wind turbines, it is essential to have an airfoil which can generate high lift. For transonic applications such as transport aircrafts and passenger aircrafts, it is essential to minimise drag [2]. This is mainly due to the presence of induced drag which would hamper the performance of the aircrafts with increase in lift. Induced drag arises due to the presence of wing tips. Although the airfoil analysis done is by considering an infinite wing with no wingtips, an airfoil which generates less pressure drag would be more suitable for transonic applications. Induced drag can be addressed by varying the geometry or by increasing the aspect ratio of the wing surface. Increasing the aspect ratio of the wingafter a certain point has an adverse effect on the aircraft as it affects its structural integrity. |
 |
TYPES OF AIRFOILS |
| There are different types of airfoils available for different purposes [3]. They can be broadly classified as: |
| • Symmetric airfoils |
| • Laminar airfoils |
| • Low Reynolds number airfoils |
| • Transonic airfoils |
| Low Reynolds number airfoils can be further classified on the basis of their applications into: |
| • Powered aircrafts airfoils |
| • Sailplanes airfoils |
| • Wind turbine airfoils |
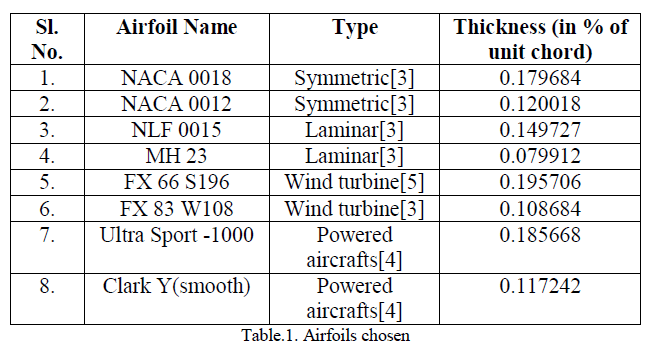
| It is essential to note that transonic airfoils are generally designed for better performances at high Mach numbers and hence, co-ordinates of such airfoils are difficult to obtain. In this research paper however, the main objective is to obtain an airfoil which has good aerodynamic characteristics for low Reynolds number applications and approximate its transonic behaviour. The types of airfoils chosen for this paper were: symmetric, laminar, powered aircraft airfoils and wind turbine airfoils. Two airfoils of contrasting geometry were chosen in order to obtain a relation between the thickness of the airfoils and its impact on its aerodynamic characteristics. The airfoils chosen for this paper are mentioned in the table below. |
 |
LOW REYNOLDS NUMBER ANALYSIS |
| In order to study the behaviour of airfoils at low Reynolds number, the software XFLR5 is used. The main characteristics required for airfoils to be used in powered aircrafts, gliders and seaplanes are. |
 |
TRANSONIC ANALYSIS USING KORN EQUATIONS |
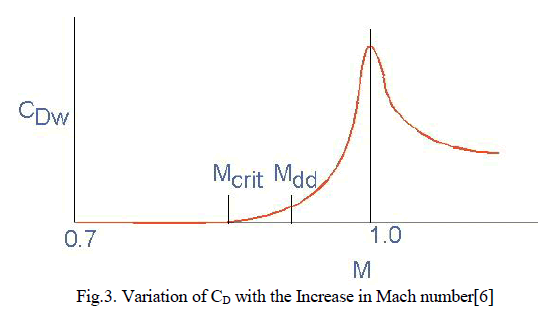
| It is difficult to analyse transonic behaviour of multiple airfoils using conventional CFD software. It is however essential to know the Drag Divergence Mach Number and the Critical Mach number of the airfoil. Critical Mach number of an airfoil is defined asthe lowest Mach number at which the airflow over some point of the aircraft reaches the speed of sound, but does not exceedit. Drag divergence Mach No. of an airfoil is defined as the Mach number at which the aerodynamic drag on an airfoil or airframe begins to increase rapidly as the Mach number continues to increase. As shown in the graph below, Critical Mach Number precedes the Drag Divergent Mach No. |
 |
| A rough approximation of the Critical Mach Number (MCr) and the Drag Divergence Mach Number (MDD) of an airfoil can be obtained through Korn Equation[7] given by the formula below. |
 |
| It is to be noted that this serves only as an approximation to estimate the Wave Drag of the airfoil at high Mach Numbers. The profile drag of the airfoil at such velocities however cannot be obtained. Since wave drag is the most predominant form of drag in such velocities [2], it can be safely assumed that lower the wave drag, better the performance. The Drag divergence Mach no. and the critical Mach no. of the airfoils are also evaluated. Higher the value of the drag divergence Mach no., there will be a significant delay in the formation of the shock. |
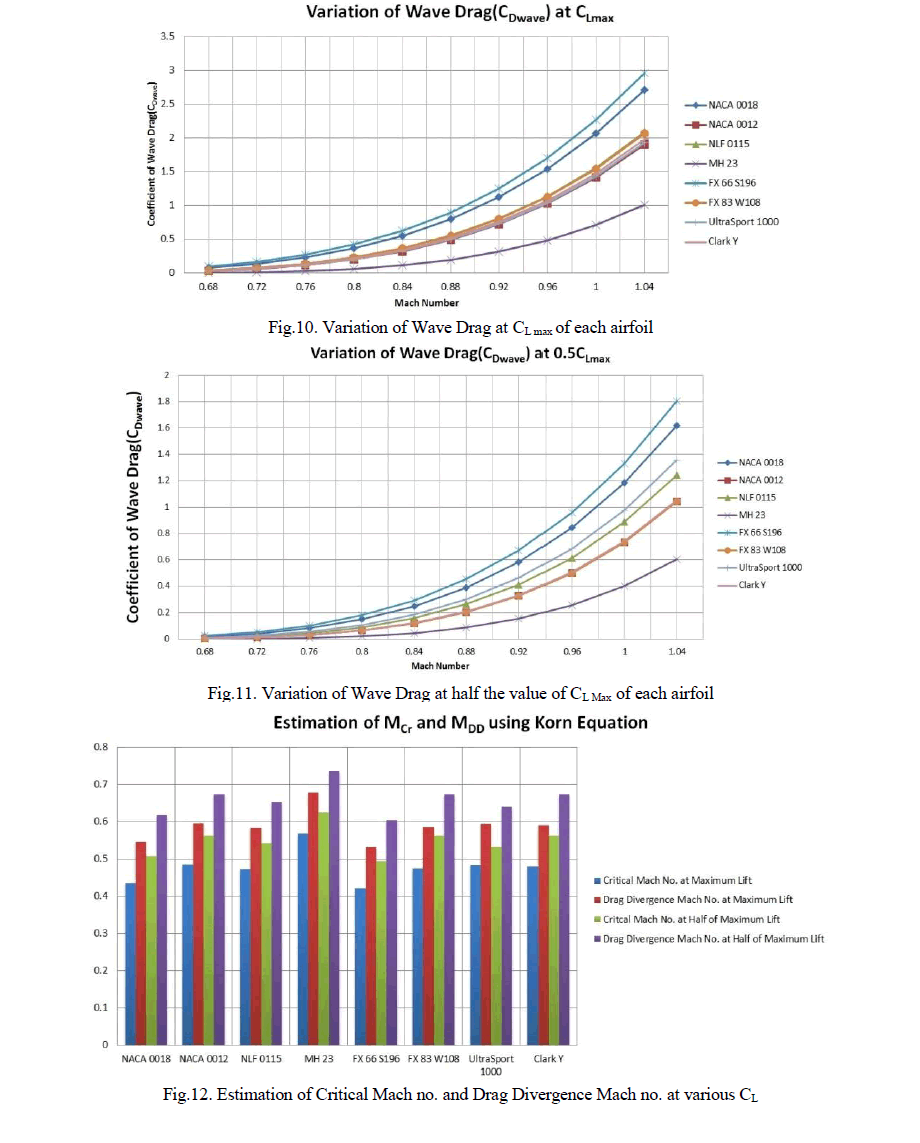
| The selected airfoils were evaluated between the Mach numbers of 0.68 to 1.04 with an interval of 0.06. In order to avoid complications, the airfoils are assumed to have a unit chord length. Due to the presence of CL in equation 1, it becomes rather difficult to assess the appropriate CL at which the airfoils must be evaluated at. Utilising a common CL for all the cases would cause a conundrum as the airfoils with the lowest values of thickness ratio would show lower values of wave drag in comparison to its thicker counterparts. In order to avoid this, the wave drag was evaluated for two separate values of CL. Each airfoil was evaluated first at its CL Max and 0.5CL Max obtained through the XFLR5 analysis. This gives a more accurate view of the airfoil performance since the CL Max utilised varies with the airfoil. |
| It was noticed that the MH 23 airfoil had the lowest value of CD Wave when evaluated at its CL Max and at 0.5CL Max. The FX 66 S196 airfoil had the highest value of wave drag at its CL Max and 0.5CL Max. The NACA 0012 and FX 83 W108 airfoils however showed significant reduction in wave drag at their respective 0.5CL Max. The MH23 airfoil was also found the have the highest values for both critical Mach no. and drag divergence Mach no. at maximum lift value and half of the maximum lift value. |
RESULTS AND DISCUSSION |
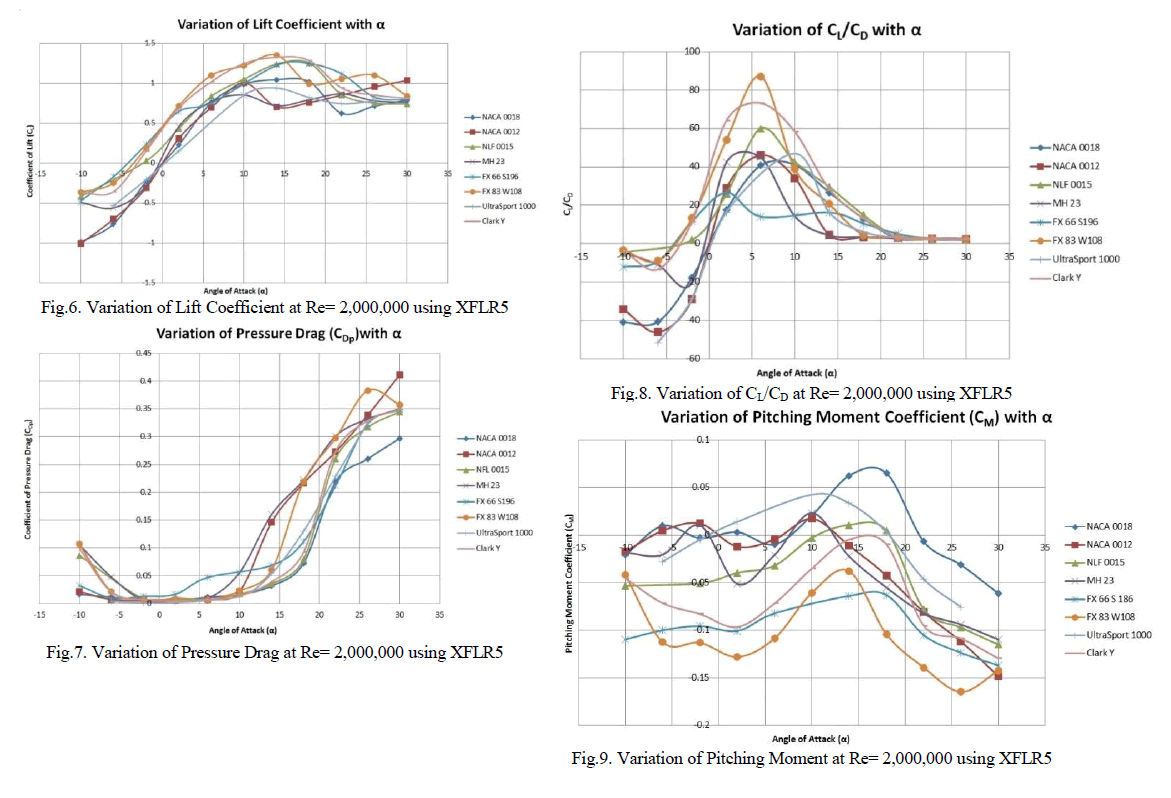
| The FX 83 W108 airfoil can be considered as the best airfoil to utilise for applications in both the Low Reynolds Number regime and at transonic conditions. It had the highest CL max, (CL/CD) max and had the lowest value of CM. It had also shown significant improvement in reduction of it wave drag as its CL Max was halved. The halved value of CL max was found to be at around 0.8897. The MCr and MDD were found to be very low at maximum lift. However, at the half of maximum lift, both the MCr and MDD had increased. This is beneficial as at a CL of 0.8897, the FX 83 W108 airfoil has an MDD of 0.672346. |
| The NACA 0018 airfoil showed the poorest performance under both transonic and low Reynolds number regime as it lacks the required qualities such as the high CL max, (CL/CD) max and low CM. It did however have one of the lowest values of CDp. It showed very poor performance at transonic conditions however with its very high value of CD wave. It also showed very low values of both MCr and MDD. This could be due to the thick and symmetric nature of the airfoil. |
| The NACA 0012 airfoil showed poor performance at low Reynolds number. However, at transonic conditions, it had a relatively low value of CDwave at half its maximum lift value which corresponds to 0.77665. It also showed a considerable increase in the values of its MCr and MDD when the maximum lift value was halved. Its low value of wave drag and its high values of MCr and MDD can be attributed to the thin profile of the airfoil. Its poor performance at low Reynolds number however may be due to the symmetric nature of the airfoil. |
| The NLF 0015 airfoil shows an average performance at both low Reynolds number and at transonic conditions. |
| The MH 23 airfoil shows a very poor behaviour at low Reynolds number with low values of CL max, CDp, (CL/CD) max and positive values of CM. However, it shows a very low value of CD wave and has the highest values of MCr and MDD at transonic conditions. This is mainly due to the very low thickness of the MH 23 airfoil and its very low value of camber. |
| The FX 66 S196 airfoil shows an average behaviour at low Reynolds number but has a very low value of CM at high angles of attack. It has the highest value of CD wave, but very low values of MCr and MDD at transonic conditions. This may be due to the high thickness and camber values of the airfoil. |
| The UltraSport 1000 airfoil demonstrates a relatively poor behaviour at low Reynolds number and has an extremely high value of CM. It does have an average behaviour at transonic conditions due to its thickness. |
| The Clark Y airfoil performs very well at low Reynolds number with high values of CL max, CDp, (CL/CD) max and relatively low values of CM. It also shows relatively low value of CD Wave at transonic conditions in spite of its Maximum value of CL being 1.6234 and its halved value being 0.8162. The Clark Y airfoil also shows a high value of MCr and MDD at high values of CL. This could be due to the thin nature of the airfoil. |
CONCLUSION |
| The FX 83 W108 airfoil and the Clark Y airfoil are shown to have the adequate requirements for both low Reynolds number application and transonic application. This is due to their high values of CL, (CL/CD) max and low values of CM at low Reynolds number. At transonic conditions, the airfoils exhibit low values of CD wave, high values of MCr and MDD. |
| The main advantage of the FX 83 W108 airfoil lies in its high values of CL and (CL/CD) max and its low values of CM at very high angles of attack. The advantage of the Clark Y airfoil lies in its relatively higher value of MCr and MDD than the FX 83 W108 airfoil. Based on the requirements of the application, the airfoil must be chosen. |
| However, the Korn equation can only act as an approximation of the transonic behaviour. Due the nature of the Korn equation, thinner airfoils and transonic airfoils generally develop an advantage over the rest. The utilization of maximum lift generated at a fixed Reynolds number of 2,000,000 was useful in providing a fair assessment. Utilizing a coefficient lift generated by an airfoil at a given Reynolds number can give use a more clear approach towards evaluation of airfoils at transonic conditions using Korn equation. If a fixed value of CL were to be used, the thinner airfoils will show higher values of MDD and MCr which may not give a clear picture on the performance of the airfoils. An experimental analysis of the airfoils in a wind tunnel at both low Reynolds number conditions and transonic conditions is however necessary to further validate this claim. |
ACKNOWLEDGEMENT |
| The author would like to acknowledge Mr. Sabari Girish S., 2013-15 Batch of M.E. Aerospace Engineering, Indian Institute of Science, Bangalore, for his invaluable help regarding the understanding of Korn equation. The author would also like to extend his gratitude to his friends Ms SrihariniTadepalli, Mr B.S. Prabhakar, Mr Neeraj Rajesh, Ms Swathi Suresh and Ms K.C. Niveditha for their unconditional support, motivation and timely assistance during the times of adversity faced during the completion of this research paper |
References |
|
 |
 |
 |