e-ISSN: 2319-9849
e-ISSN: 2319-9849
1Department of Chemistry, HNB Garhwal University, Srinagar, Garhwal, Uttarkhand, India.
2Department of Chemistry, Bipin Bihari College, Jhansi, Uttar Pradesh, India.
Received date: 15/07/2014; Revised date: 04/08/2014; Accepted date: 07/08/2014
Visit for more related articles at Research & Reviews: Journal of Chemistry
The preparation of parchment supported inorganic precipitate lead tungstate model membrane has been explained. The membrane potentials of inorganic membrane were measured with uni-univalent electrolytes (KCl, NaCl and LiCl) using saturated calomel electrodes (SCEs). The TMS method was used for the evaluation of the effective fixed charge density of the membrane. The order of surface charge density for electrolytes used is found to be KCl>NaCl>LiCl. The potential data have been used to characterize the membrane behaviour in contact with various electrolytes solutions, as well as to calculate the transference number of ions and permselectivity of the membrane. Thermodynamically effective fixed charge density has also been evaluated using the theories TMS, Kobatake et al. and Tasaka et al. based on the principles of irreversible thermodynamics. Theoretical predictions were borne out satisfactorily by our experimental results. The membrane is characterized by SEM, XRD, TGA and FTIR techniques.
Fixed Charge density, permselectivity, lead tungstate membrane, SEM, XRD, FTIR and TGA
Membranes allow transmission of charged and uncharged species with varying degrees of restriction. The relative case with which charged species migrate through a membrane is commonly expressed in terms of permselectivity[1-3]. A membrane is said to be ideally ion selective if only either positively or negatively charged ions pass through it, on the other hand if migration of ions through a membrane is not affected at all, the membrane is said to be non-selective. Most often the membrane are neither ideally ion selective nor entirely non-selective in nature; they exhibit ion selectivity in some measure depending on the nature of the membrane forming material, its dimensional and electrochemical characteristics. Membrane potential studies are commonly used for the electrochemical characterization of membrane[2-3]. This paper describes the preparation of lead tungstate model membrane. Various membrane parameters including thermodynamically affective fixed charge density have been evaluated from membrane potential measurements by using TMS[4,5,6] Kobatake et al.[6,7] and Tasaka et al.[8] procedure based on the thermodynamic irreversible processes.
Preparation of membrane
Parchment supported inorganic precipitate lead tungstate synthetic membrane has been prepared by the method of interaction as suggested by Ansari and coworkers[9,10]. To precipitate these substances in the interstices of parchment paper, a 0.2M solution of sodium tungstate (S. D. Fine Ltd.) was placed inside glass tube, to one end of which was tied the parchment paper (supplied by Amol group of companies, Mumbai, India) previously soaked in deionised water. The tube was suspended for 72 hours in a 0.2 M solution of lead nitrate (Ranbaxy). The two solutions (fresh solution) were interchanged later and kept for another 72 hours. Thus parchment paper and inorganic precipitate as a whole acts as a synthetic membrane. The membrane thus prepared was washed with deionized water to remove free electrolytes.
Measurement of membrane potential
| SCE | Solution C1 | Lead tungstate Membrane | Solution C2 | SCE |
The electrochemical cell of the type was used for measuring membrane potential (Em) arising through the membrane by maintaining a tenfold difference in concentration (C1 /C2=10) and using a multimeter (Rishmulti(R) 43/4 digits 18S). All the electrolyte solutions used in the investigation were prepared from analytical grade reagents and deionized water.
Characterization of membrane
The expected performance of an ion exchange membrane is its complete characterization, which involves the determination of all those parameters that affect its electrochemical properties. These parameters are the membrane water content, porosity, thickness, swelling etc. and were determined as described elsewhere[11].
Water uptake (% total wet weight)
The membrane was soaked in deionized water for 2 hour blotted quickly with whatmann filter paper to remove surface moisture and immediately weighted. These were further dried to a constant weight in vacuum over P2O5 for 24 hour. The water uptake (total wet weight) was calculated as follows
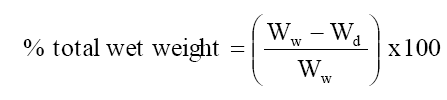
Where Ww is the weight of the soaked or wet membrane and Wd the weight of the dry membrane.
Porosity
Porosity was determined as the volume of water incorporated in the cavities per unit membrane volume from the water uptake data:
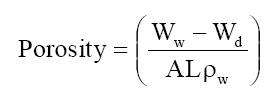
Where A is the area of the membrane (cm2). L the thickness of the membrane (cm) and ρw the density of water (g/cm3).
Thickness
The membrane thickness value was averaged from six measurements different locations on the effective surface region of the membrane using a micrometer.
Swelling
Swelling was measured as the difference between the average thickness of the membrane equilibrated in 1M NaCl for 24 hour and the dry membrane.
Scanning Electron Microscopy (SEM) studies
The surface morphology of parchment supported lead tungstate membrane was analysed with scanning electron microscope (Philips 515 USA). A gold Sputter coating was carried out on the desired membrane sample at pressure 1 Pa.
The FTIR spectrum of parchment supported lead tungstate membrane was done by Perkin Elmer instrument (Spectrum BX series, USA). The entrance and exit beam to the sample compartment was sealed with a coated KBr window and this was a hinged cover to seal it from the environment.
X-ray diffraction pattern of the parchment supported lead tungstate membrane was recorded by Miniflex-II X-ray diffractrometer (Rigaku Corporation) with Cuk ◻◻ radiation.
Thermogravimetric analysis (TGA) studies
The degradation process and thermal stability of the membrane was investigated using thermogravimetric analyzer (Perkin Elmer, Pyris Diamond), under nitrogen atmosphere (200 ml/min.) using a heating rate of 100C min-1 from 250C to 11000C.
The result of water content, Porosity thickness and swelling of parchment supported inorganic precipitate lead tungstate membrane are summarized in Table 1. The water content of a membrane depends on the vapour pressure of the surroundings. In case of most of the transport measurements, only the membrane water content at saturation is needed, and that too mostly as a function of solute concentration. Thus low order of water content swelling and porosity with less thickness of membrane suggests that interstices are negligible and diffusion across the membrane would occur mainly through exchange sites[12,13].
The SEM surface image of parchment supported lead tungstate membrane is presented in Fig. 1. It can be seen that the membrane is heterogeneous in nature as well as dense with no visible cracks. SEM image (Fig. 1) appears to be composed of dense and loose aggregation of small particles and formed pores probably with non-linear channel but not fully inter connected. Particles are irregularly condensed and adopt a heterogeneous structure composed of masses of various sizes.
The FTIR spectra of the parchment supported membrane has provided in Fig. 2. The membrane contains various characteristic peaks. The spectra exhibits various strong to medium or weak intensity band, such as 3421, 2919, 2851, 2425, 1765, 1383 and 1621 (Cm-1) characteristic of the functions present in the inorganic precipitate membrane.
X-Ray scattering techniques are a family of non-destructive analytical technique which reveal information about the crystallographic structure, chemical composition and physical properties of materials. Fig. 3 shows X-ray diffraction spectrum of the lead tungstate membrane. The material recorded in powdered sample exhibited some sharp peaks in the spectrum shows semi-crystalline nature of the material.
The thermal stability of the lead tungstate membrane was analyzed by TGA. The TGA curve measured under flowing nitrogen is reported in Fig. 4 TGA of the membrane material showed gradual weight loss of a about 3 percent to 11 percent from 4000C to 5800C which may be due to the removal of external water molecules present at the surface of the membrane material. Further weight loss of 15 percent to 20 percent from 8000C to 10000C indicating the start of condensation due to the removal of the lattice water from the material.
The values of membrane potential across lead tungstate membrane in contact with various 1:1 electrolytes are given in Table 2 and plotted against log (C1 + C2)/2 in Fig. 5.
The values of the membrane potentials are low when the membrane is used to separate concentrated solutions of electrolytes, whereas it increases till it reaches a maximum as the solutions across the membrane are diluted. The increase in membrane potential with the decrease in he electrolyte concentration may be ascribed to the structural changes produced in the electrical double layers at the membrane solution interfaces and the ionic atmosphere within the pores[14].
The fixed group present in a well-characterized ion exchange membrane can easily be estimated by titration[15]. Lakshminarayanaiah[16] used the isotopic and potentiometric methods to evaluate the apparent fixed charge on parlodion membranes. In this study, the tirtration method proved inconvenient and inaccurate, and the isotopic method was discarded in view of the strong ionic adsorption phenomenon exhibited by the system. Consequently the potentiometric method based on the fixed charge concept of Toerell[4] and Meyer and Sievers[5] the important features of which have been reviewed by Lakshminarayanaiah[16], was used.
According to this theory, total membrane potential is considered to be made up of a diffusion potential within the membrane and two interfacial (Donnan) potentials at the membrane-solution interfaces. The total membrane potential Em in millivolts according to this theory, applicable to a highly idealized system at 250C is given by the equation.
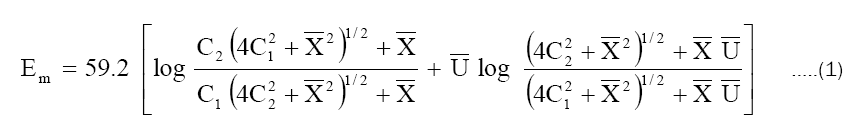
where 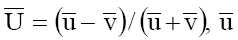 and
and 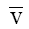 are the mobilities of the cation and anion respectively in the
membrane, expressed in equivalents/litre of imbibed solution. In order to evaluate this parameter for the
simple case of 1:1 electrolyte and membrane carrying a net negative charge of unity
are the mobilities of the cation and anion respectively in the
membrane, expressed in equivalents/litre of imbibed solution. In order to evaluate this parameter for the
simple case of 1:1 electrolyte and membrane carrying a net negative charge of unity 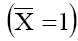 , theoretical
concentration potential Em across the membrane were calculated as a function of C2 , the ratio
(C1 + C2) being kept at a constant value of 10 for different mobility ratio
, theoretical
concentration potential Em across the membrane were calculated as a function of C2 , the ratio
(C1 + C2) being kept at a constant value of 10 for different mobility ratio 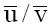 . The observed membrane
potential for different electrolytes were also plotted in the same graph as a function of log (1/C2). The
experimental curve shifted horizontally and tan parallel to one of the theoretical curves. The extent of this
shift give log
. The observed membrane
potential for different electrolytes were also plotted in the same graph as a function of log (1/C2). The
experimental curve shifted horizontally and tan parallel to one of the theoretical curves. The extent of this
shift give log 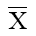 and the parallel theoretical curves gives the value for
and the parallel theoretical curves gives the value for 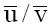 . The valuesof
. The valuesof 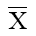 x102 and
x102 and 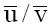 derived in this way for KCl, NaCl and LiCl electrolytes are: 3.6, 1.5, 4.6 and 1.0, 0.8, 0.6 respectively.
derived in this way for KCl, NaCl and LiCl electrolytes are: 3.6, 1.5, 4.6 and 1.0, 0.8, 0.6 respectively.
Using the fixed charge concept of Toerell-Meyer-Sievers (TMS) theory[4,5] for membrane potential and the basic flow equations provided by nonequilibrium thermodynamics, Kobatake et al.[6] have derived the following expression for membrane potential Em:
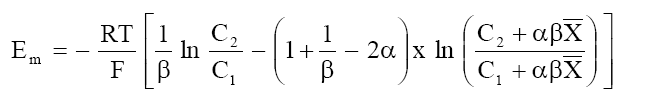 (2)
(2)
where 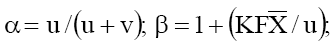 and K is a constant dependent upon the viscosity of the
solution and structural details of the polymer network of which the membrane is composed. To evaluate
the membrane parameters α,β and
and K is a constant dependent upon the viscosity of the
solution and structural details of the polymer network of which the membrane is composed. To evaluate
the membrane parameters α,β and 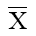 , two limiting forms of eq. (2) were derived. When the external salt
concentration C is sufficiently small,
, two limiting forms of eq. (2) were derived. When the external salt
concentration C is sufficiently small,
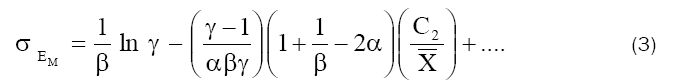
where
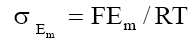
and γ=C2/C1
When the salt concentration C is high,
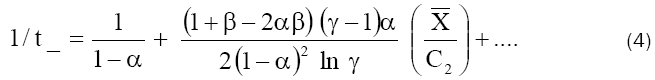
Here t_ is apparent transference number of the coion (anion) in a negatively charged membrane defined by
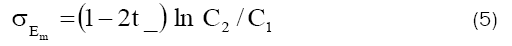
The values of t_ calculated from observed membrane potentials using eq. (5) are given in Table 3.
Eq. (3) was used to get the value of β and a relation between α and  by evaluating the intercept and the initial slope of a plot of σEm against C2 (Fig. 6), while eq. (4) was used to evaluate α from the
intercept of a plot of 1/t_ against 1/C2 (Fig. 7). The value of
by evaluating the intercept and the initial slope of a plot of σEm against C2 (Fig. 6), while eq. (4) was used to evaluate α from the
intercept of a plot of 1/t_ against 1/C2 (Fig. 7). The value of  were determined by inserting this value of α in the relation between α and
were determined by inserting this value of α in the relation between α and 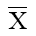 obtained earlier. The value of
obtained earlier. The value of 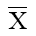 derived in this way for lead tungstate memrbane in contact with various 1:1 electrolytes are given in Table (4-5). Kobatake and Kamo
proposed a simple method for the evaluation of effective fixed charge density of membranes using the
following equation for permselectivity Ps.
derived in this way for lead tungstate memrbane in contact with various 1:1 electrolytes are given in Table (4-5). Kobatake and Kamo
proposed a simple method for the evaluation of effective fixed charge density of membranes using the
following equation for permselectivity Ps.
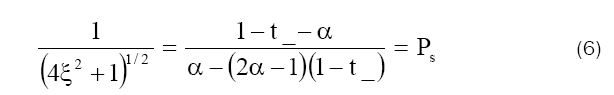
where
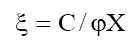
This equation has been used to find the permselectivity Ps from the membrane potential
measurements by a number of investigators, if the transport number of coions t_ is while if the transport
number of coions has the free solution value, Ps=0. The value Ps (Table 6) obtained using the right hand
side of eq. (6) were plotted against log C. The concentration at whith Ps 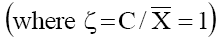 become
become 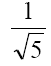 gives the value of thermodynamically effective fixed charge density
gives the value of thermodynamically effective fixed charge density 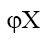 as required by the left hand side of eq. (6) Fig. 8 represents plots of Ps vs log (C1+ C2)/2 for the lead tungstate membrane in
contact with 1:1 electrolytes. The value of
as required by the left hand side of eq. (6) Fig. 8 represents plots of Ps vs log (C1+ C2)/2 for the lead tungstate membrane in
contact with 1:1 electrolytes. The value of 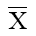 thus derived for the membrane and 1:1 electrolytes are
given in Table 7.
thus derived for the membrane and 1:1 electrolytes are
given in Table 7.
Tasaka et al.[8] derived an equation for the membrane potential across a charged membrane. The total membrane potential Em was considered as the sum of a diffusion potential Ed inside the membrane and the electrostatic potential different Ee between the membrane surfaces and the electrolyte solutions on both sides of the membrane. The diffusion potential Ed was obtained by integrating the basic flow equation for diffusion while the electrostatic potential difference was calculated from the Donnan theory, stated mathematically.
Em = Ed + E c (7a)
where
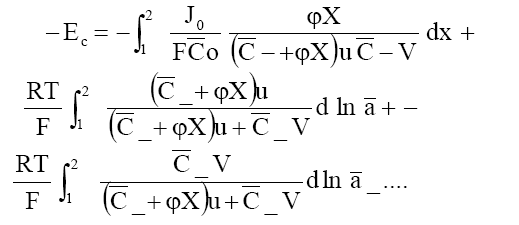 (7b)
(7b)
Where a1 and a2 are the activities of the electrolytes on the two sides of the membrane, bars indicate the membrane phase, J0 is the flow of electrolyte in the absence of an external electric field and other symbols have their usual significance. Integrating eq. (7) in the limit of high electrolyte concentrations across the membrane, one obtains the following equation for the membrane potential:
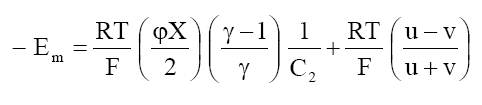
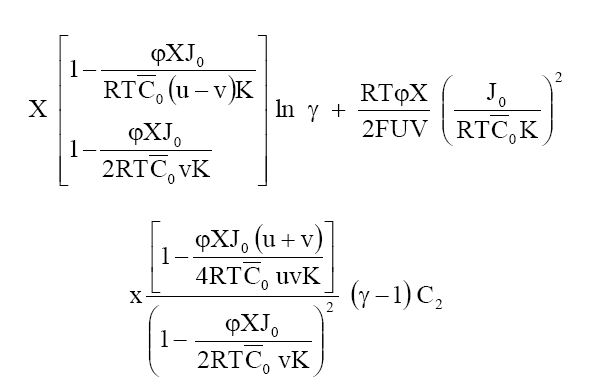 (8)
(8)
At high electrolyte concentration, eq (8) can be approximated to
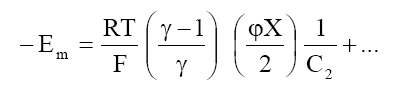 (9)
(9)
eq. (9) predicts a linear relationship between Em and 1/C2 from which 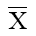 can be calculated. Plots of Em Vs 1/C2 (Fig. 9) are in agreement with eq. (9). The values of
can be calculated. Plots of Em Vs 1/C2 (Fig. 9) are in agreement with eq. (9). The values of 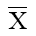 derived from the slope of lines are given in Table 7.
derived from the slope of lines are given in Table 7.
The water content of a model membrane depends on the vapour pressure of the surroundings, low order of water content swelling and porosity with less thickness of membrane suggests that interstices are negligible and diffusion across the membrane would occur mainly through exchange sites. The membrane is heterogeneous in nature as well as dense with no visible cracks. The membrane material exhibits some sharp peaks in the spectrum shows semi-crystalline nature of the material.
The values of the effective fixed charge densities evaluated from the different methods are almost the same. The slight deviations may be because of the different procedure adopted for the evaluation. It may, therefore, be concluded that the methods developed recently for the evaluation of effective fixed charge density are valid for the membrane under investigation.
The authors are gratefully acknowledge the head Dept. of chemistry H.N.B. Garhwal University Garhwal for providing necessary research facilities.