ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
K.Anitha 1, Dr.P.Venkatesan 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Feature Selection the process of finding the optimal subset for a given supplied data. In this paper we discuss about basic concepts and applications of Rough Set Theory in Feature Selection. The main advantage of Rough Set Feature Selection is it requires no additional parameters other than the original data. Rough Set is especially useful for domains where data collected are imprecise or incomplete about the domain objects. In this paper Quick-Reduct Algorithm is used to reduce the number of genes from gene expression data.
Keywords |
| Rough Set , Attribute Reduction, Feature Selection, Quick-Reduct Algorithm. |
INTRODUCTION |
| It is estimated that every 20 months or so the amount of information in the world doubles. At the same time tools used for various knowledge fields must be developed to overcome this growth. Knowledge Management is the only solution for this growth. Knowledge Discovery in Databases (KDD) is the nontrivial process of identifying valid, novel and useful patterns of data. Traditionally data was changed in to knowledge by means of analysis and interpretation. We need a technique that can reduce the dimensionality using the information contained within the dataset and also preserve the meaning of the dataset (Knowledge). Rough Set theory can be used as such a tool to discover data dependencies and reduce the number of attributes using the data alone . |
FUNDAMENTALS OF ROUGH SET THEORY |
| In Rough Set theory , an Information System is defined as a pair , IS = (U, A) where U is finite non-empty set which is called the Universal Set and A- set of Attribute which is also finite and non-empty. Each attribute a ïÿýïÿý A is associated with a set Va of its value, called domain of a. We can separate the attribute set into two non-empty disjoint subset C and D where C is the conditional set and D is the decision set. |
INDISCERNIBILITY |
| With any P ⊆ A, there is an associated equivalence relation IND(P) which is defined as follows: |
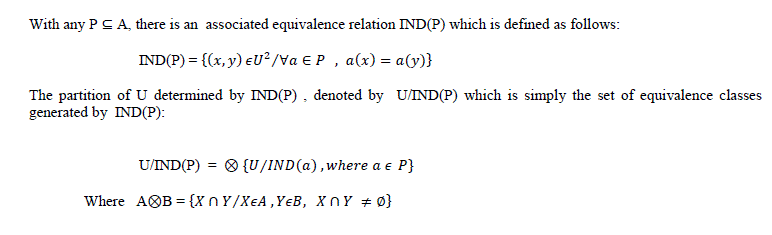 |
LOWER AND UPPER APPROXIMATION |
| For any concept X⊆ ïÿýïÿý the attribute subset P ⊆ ïÿýïÿý , X could be approximation by the P- Upper and Lower approximation using the knowledge of P. The lower approximation of X is the set of objects of U that are surely in X , where as the upper approximation of X is the set of objects of U that are possibly in X. The upper and Lower approximations are defined as follows |
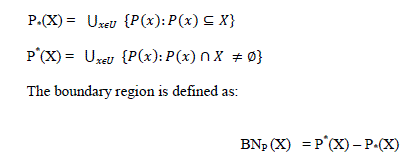 |
| If the boundary region is empty that is upper approximation is equals to lower approximation, concept X is said to be P definable or else X is a Rough Set with respect to P. |
POSITIVE REGION |
| The Positive Region of decision class U/IND(P) with respect to conditional attribute C is denoted by |
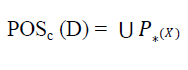 |
| The following diagram defines the diagrammatic representation of Rough Set Theory |
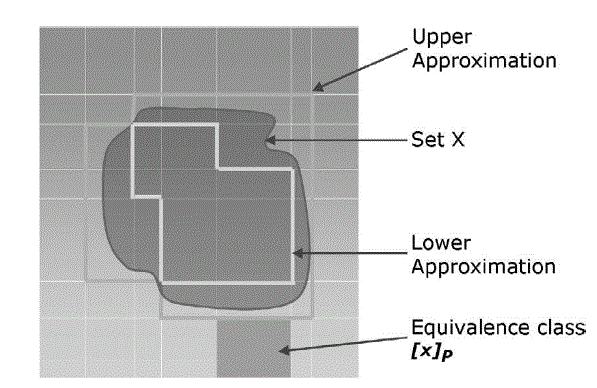 |
REDUCT |
| In many application problem it is often necessary to maintain a concise form of the information system. One way to implement this is to search a minimal representation of original data set. Reduct is a minimal subset R of initial attribute set C(conditional) such that for a given set of decision attribute D |
| In other words, reduct is the minimal set of attributes preserving positive region. There may exists many reducts for an Information System. |
CORE |
| The Core is the set of attributes that are contained by all Reducts which is defined as follows: |
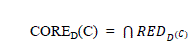 |
| In other words, CORE is the set of attribute that cannot be removed without changing the positive region. |
IMPORTANTS OF FEATURE SELECTION |
| For many applications manual analysis of data is slow, costly and highly subjective. Indeed, as data volumes grow dramatically, manual data analysis is becoming completely impractical in many domains. This motivates the need for efficient, automated knowledge discovery. The following are the step by step process of KDD |
| Selection of Data |
| Data Cleaning |
| Reduction of Data |
| Data Mining |
| Data Interpretation. |
| The high dimensionality of databases can be reduced using suitable techniques, depending on the future KDD process. There are two feature qualities that must be considered by Feature Selection Methods. They are Relenvancy and Redundancy. A feature is said to be relevant if it is predictive of the decision feature(s); otherwise, it is irrelevant. A feature is considered to be redundant if it is highly correlated with other features. An informative feature is one that is highly correlated with the decision concept(s) but is highly uncorrelated with other features. |
DIMENSIONALITY REDUCTION |
| The Dimensionality Reduction techniques are classified into two categories Linear and Non-Linear. Linear methods include Principle Component Analysis (PCA) and multi dimensional scaling .These techniques are used to determine Euclidean Structure of a dataset’s internal relationship. PCA transforms the original features of a dataset to a (typically) reduced number of uncorrelated ones, termed principal components. If an algorithm performs FS independently of any learning algorithm then it is a Filter approach. Filters tend to be applicable to most domains as they are not tied to any particular induction algorithm. RELIEF, FOCUS, LVF, SCRAP,EBR are some of the filter based reduction techniques. If the evaluation procedure is tied to the task (e.g., classification) of the learning algorithm, the FS algorithm employs the wrapper approach. This method searches through the feature subset space using the estimated accuracy from an induction algorithm as a measure of subset suitability. LVW (Las vegas wrapper), Genetic Algorithm, SAFS are wrapper based approaches. |
QUICK – REDUCT ALGORITHM |
| Quick Reduct Algorithm is an efficient algorithm for finding reduct. This is widely used is several soft computing implementations using Rough Sets. Quick Reduct algorithm proposed by A.Chouchoulas and Q.Shen. Quick-Reduct Algorithm attempts to calculate a reduct without exhaustively generating all possible subsets. It starts off with an empty set and adds in turn, one at a time, those attributes that result in the greatest increase in the rough set dependency metric, until this produces its maximum possible value for the dataset. |
QUICK REDUCT ( C , D ) |
 |
DATA SET |
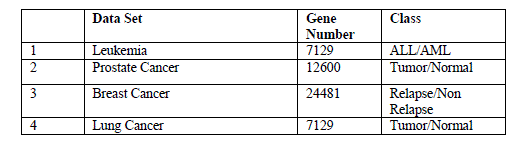
| Datasets: leukemia, breast cancer, lung cancer and prostate cancer which are available in the website: http://datam.i2r.a-star.edu.sg/datasets/krbd/, the gene number and class contained in four datasets are listed in Table 1 |
 |
CONCLUSION |
| In this paper Rough Set based Quick-Reduct Algorithm have been used to reduce the gene expression data. It gives the minimal reduct set for the given data set. We can use it for Car data set, Mammogram Image Analysis, Iris- Thyroid information system and so on. |
References |
|