Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fixed point Theorem in Intuitionistic Fuzzy metric space

M.S. Chauhan1 Dheeraj Aheere2 Bharat Singh3
 Asst. Prof. Rajabhoj Govt. College,Mandideep Dist. , Raisen (M. P. ) India1
Research Scholar, Vikram University, Ujjain (M. P) India2
Reader, SOC & E IPS Academy Indore (M. P. ) India3
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this paper ,we generalize fuzzy metric space in term of fixed point theorem in modified Intuitionistic fuzzy metric space using weakly compatible mapping along with property (CLRS) and (CLRT).

Keywords
fixed point, intuitionistic fuzzy metric, implicit relation, compatibility

INTRODUCTION
Aanassov[2] Introduction in studied the concept of Intuitionistic fuzzy set as a noted generalization of fuzzy set which has inspired intense research activity around this newly introduced notion. Recently Park[7] using the idea of Intuitionistic fuzzy sets. Defined Intuitionistic fuzzy metric spaces as a generalization of fuzzy metric spaces due to George and Veeramani[4] and also proved some basic results which include Baire’s theorem and uniform limit theorem besides some other core results. Afterthat ,Saadati and Park[8] defined precompact sets in Intuitionistic fuzzy metric spaces and proved that any subset of an Intuitionistic fuzzy metric space is compact if and only if it is precompact and complete.They also defined topologically complete Intuitionistic fuzzy metrizable space and proved that any G�� set in a complete Intuitionistic fuzzy metric space is a topologically complete Intuitionistic fuzzy metrizable space and vice versa.George and veeramani [11] modified the concept of fuzzy metric space due to Kramosi and Michalek [6] and defined a Hansdorff topology on modified fuzzy metric space which often used In current researches. Grabiee [5] extended classical fixed point theorems of Banach and Edelstein to complete and compact fuzzy metric spaces respectively. The theory of fuzzy sets was initiated by Zadeh [13]. In the last four decades, like all other aspects of Mathematics various authors have introduced the concept of fuzzy metric in several ways.

II. PREMILIRIES
for all x,y ,z,x’ and y’∈L*.

III. MAIN RESULTS
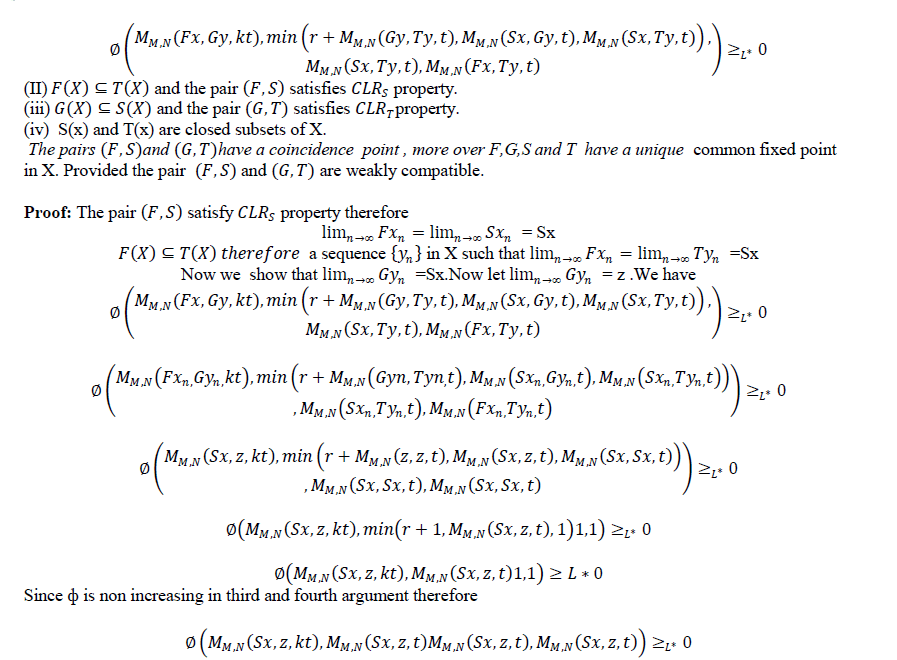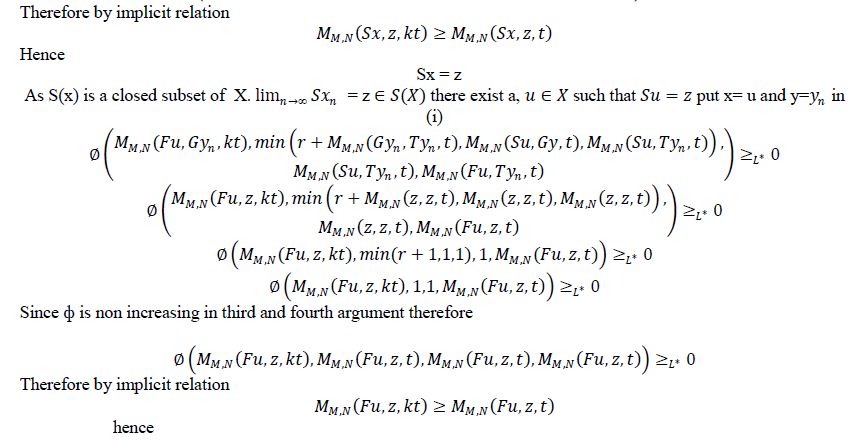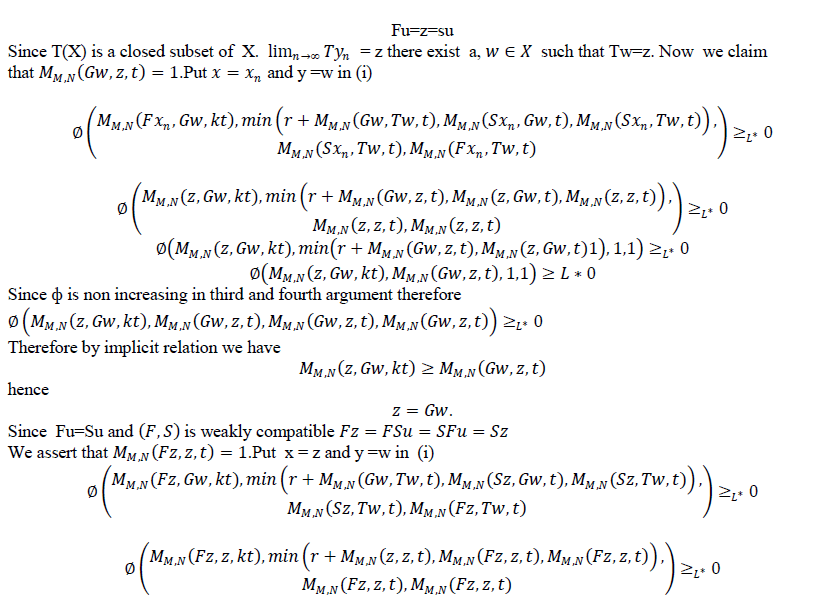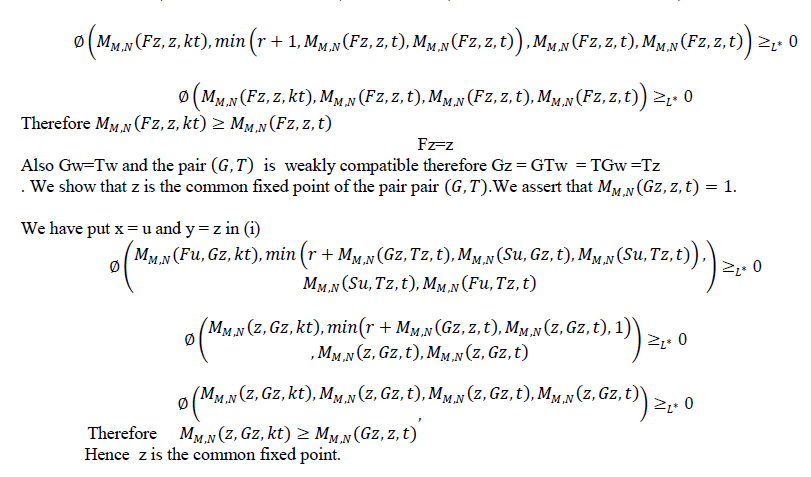Theorem 3.2 Let f,g,S and T be self mappings of a modified IFMS (X,M,T) satisfying the conditions(i-iv) of theorem 3.1.suppose that
(v) S(X) (orT(X)) is a closed subset of X.
Then the pairs (f,S) and (g,T) have a coincidence point. Moreover, f,g,S and T have a unique common fixed point in X provided that the pairs (f,S) and (g,T) are weakly compatible.
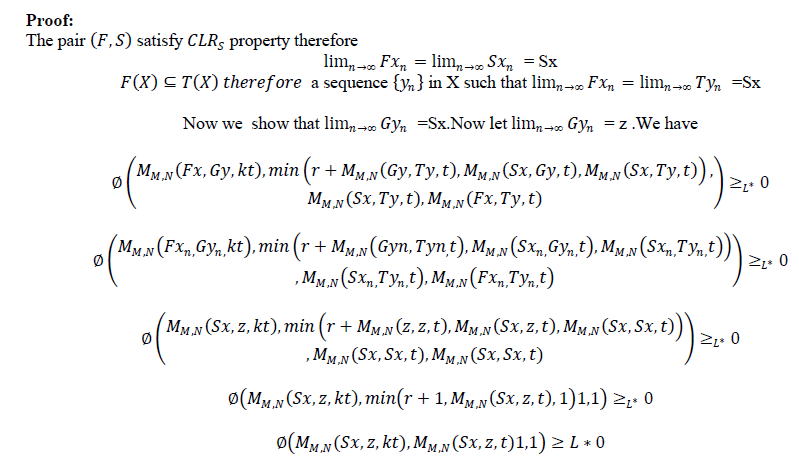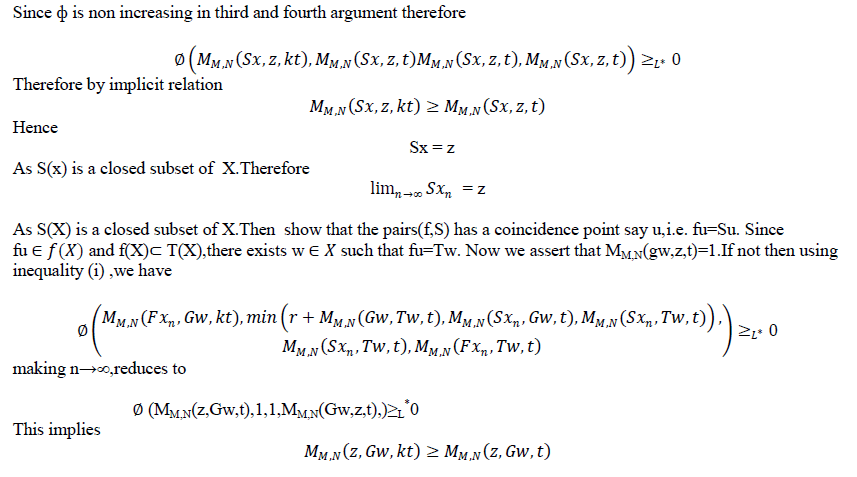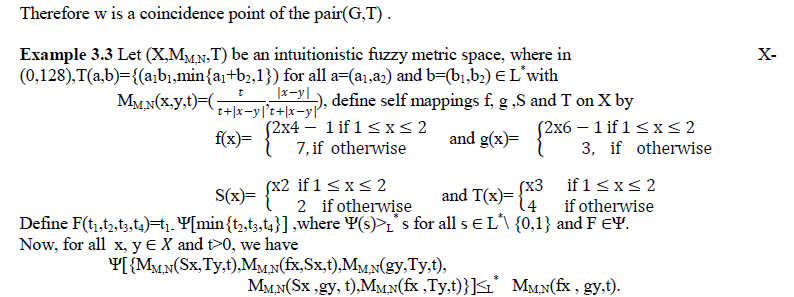Which demonstrates the verification of the esteemed implicit function.

References
  1. J.Ali and M Imdad. An implicit function implies several construction conditions, Sarajevo J. Math. 17(4) (2008), 269-285.
  2. K. T. Atanassov. Intuitionistic fuzzy sets, Fuzzy Sets and Systems. 20 (1986), 87-96.
  3. G. Deschrijver and E. E. Kerre. On therelationship between some extensions of fuzzy set theory. Fuzzy Sets and Systems. 133 (2003) , 227- 235.
  4. A George, P. Veeramani, On Some results in fuzzy metric spaces, Fuzzy Sets and Systems 64 (1994), 395-399 .
  5. M. Grabee, Fix Points in fuzzy metric spaces, Fuzzy Sets and Systems. 27 (1988), 385-389.
  6. O. Kramosil and J. Michalek, Fuzzy Metric and statistical metric spaces, Kybernetica, 11 (1975), 326-334.
  7. J. H. Park, Intuitionistic fuzzy metric spaces, Chaos Solitons Fractals, 22 (2004), 1039-1046.
  8. R. Saadati and J.H. Park, On the Intuitionistic topological spaces, Chaos Solitons Fractals, 27 (2006), 331-344.
  9. R. Saadati, S. Sedghi N. Shobe, Modify Intuitionistic fuzzy metric spaces and some fix point theorems, Chaos Solitons Fractals, 38 (2008), 36-47.
  10. B. Schweizer, A. Sklar, Probabillistic Mertic Spaces, North Holland Series in probability and Applied Maths, Amsterdam, Vol. 5, (1983).
  11. W. Sintunavarat, P. Kuman, Common fixed point theorems for a pair of weakly compatible mappings in Fuzzy Metric Spaces, Journal of Applied mathematics , Vol. 2011 (2011) , Article ID 637958, 14 pages.
  12. D. Turkoglu, C. Alaca, Y. J. Cho and C. Yildiz, Common fix point theorems Intuitionistic fuzzy metric spaces, J. Appl. Math. Computing, 22 (2006), 411-424.
  13. L. A. Zadeh, Fuzzy Sets, Information Control, 8 (1965), 338-353.
  14. Manish Jain and Sanjay Kumar , A Common Fixed Point Theorem in Fuzzy Metric Space using the Property (CLRg),THAI JOURNAL OF MAHEMATICS VOLUME X (20XX) NUMBER X:XX-XX .