ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
J.Prabawathi1, Mr.R.S.Karthic2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper is devoted to the design and the physical security of a parallel dual-core flexible crypto processor for computing pairings over Barreto-Naehrig (BN) curves. The proposed design is specifically optimized for field-programmable gate-array (FPGA) platforms. The design explores the in-built features of an FPGA device for achieving an efficient crypto processor for computing 128- bit secure pairings. The work further pinpoints the vulnerability of those pairing computations against sidechannel attacks and demonstrates experimentally that power consumptions of such devices can be used to attack these ciphers. Finally, we suggest a suitable countermeasure to overcome the respective weaknesses.
INTRODUCTION |
| Bilinear pairing first used in cryptography independently by Mitsunari et al. [7], Sakai et al. [8], and Joux [9] in 2000. One year later, Boneh and Franklin solved a long lasting problem of identity-based cryptography [10] based on pairing. Since then an impressive number of proposals arrived in the literature for designing cryptographic protocols based on pairings [11]. On the other hand, steep growth of the adversary’s computation power demands increasing bit security in cryptographic protocols running in these applications. Practice has shown that one of the most efficient options to compute pairings for high bit security is to resort to Tate pairing operating on Barreto-Naehrig (BN) curves[12] defined over a 256-bit prime field having embedding degree k=12 . |
| Efficient computation of Tate pairing with linear complexity with respect to the size of the input was introduced long back in 1986 by Miller [13]. Significant improvements and the generalization of Miller’s algorithm were independently proposed in 2002 by Barreto et al. [14] and Galbraith et al. [15]. Thereafter, intensive research has been carried out for further improvement. In this paper, we extend the work presented in [16] and propose a pairing crypto processor for BN curves. The design is flexible and resistant to side-channel attack. FPGA is one of the suitable platforms for implementing cryptographic algorithms. This paper proposes new implementation techniques of addition and multiplication on FPGAs. The in-built features available inside an FPGA device have been utilized to develop a high-speed 256-bit adder circuit. We show that when utilizing such adder circuits and adopting a parallelism technique, the multiplication in can be substantially improved. Based on such arithmetic cores, we develop a parallel configurable hardware for computing addition, subtraction, and multiplication. Existing techniques to speed up arithmetic in extension fields (see [17] and [18]) for fast computation in and are used on top of it. |
PROPOSED SYSTEM ARCHITECTURE |
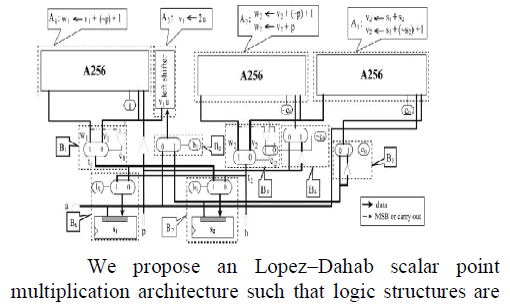 |
| implemented in parallel and operations in the critical path are diverted to noncritical paths. |
| Scalar multiplication is by far the most important operation in elliptic curve cryptosystems. ECSM is an operation which, on input an integer k and a point P on an elliptic curve C, computes another point Q such that Q = kP. In our ECSM architecture, we use a variant of the algorithm due to Lopez and Dahab, which is an improvement of the traditional Montgomery ECSM algorithm [3]. The algorithm consists of three stages: 1) conversion of P from affine coordinate to projective coordinate; 2) computation of Q = kP in projective coordinate; and 3) conversion of Q from projective coordinate back to affine coordinate. The most important operations for designing an efficient ECC processor are finite field multiplication, inversion, and squaring. Field addition and subtraction in GF(2m) are not investigated since they are defined as polynomial addition and can be implemented simply as the XOR addition of the two mbit operands [1]. Finite-field squarer over GF(2163) has been designed based on the proposal presented in [4]. For finite field multiplication, we have designed an efficient least significant digit finite-field multiplier as proposed in [5]. For inversion, an efficient inverter based on the Itoh–Tsujii multiplicative inverse algorithm [6] has been implemented. For the design of the architecture for ECSM, two different parts are considered: the first part involves calculations in the projective coordinate system, and the other part involves the calculations for converting projective coordinates to affine coordinates. For the projective calculations,parts 1 and 2 of the LD algorithm are considered. In the design of this part of the processor, as proposed in [7], the number of computational units is chosen in such a way that allows parallel computations to be performed. Hence, we use three field multipliers to implement the main loop of the algorithm in which point addition and doubling is carried out. So, according to Section 2.1 of the LD algorithm, in the the first stage, three multiplications X1 Z2, X2 Z1, and T Z2(T → X2) are performed in parallel by using three multipliers, and then three other multiplications x p Z1, X1X2T Z2 (T ← Z1), and bZ4 2 are accomplished in parallel in the second stage, as shown in Fig. 1. Hence, the delay of each iteration is reduced from six field multiplication delays to two field multiplications delays. As mentioned, the most important modules in the design of an ECSM are the field multiplier, the field inverter, and the field squarer. The key point here is that the critical path must be placed on the longest path among these modules. Since in our design the inverter module is designed in such a way that its critical path coincides with that of the multiplier’s and, since the multiplier’s path is longer than the squarer’s path, the critical path needs to be placed on the multiplier. Another important strategy in the design of the architecture for the projective calculations unit is that separate calculations are not performed for the use of the initial values of part 1 of the LD algorithm, because if further computational modules are designed for these calculations, the complexity of the critical path and the amount of required area will be increased. |
| Stages in LD Algorithm: |
| The algorithm consists of three stages: |
| Conversion of P from affine coordinate to projective coordinate; |
| Computation of Q = kP in projective coordinate; and |
| Conversion of Q from projective coordinate back to affine coordinate. |
| For the design of the architecture for ECSM, two different parts are considered: the first part involves calculations in the projective coordinate system(X1,X2,Z1 and Z2), and the other part involves the calculations for converting projective coordinates to affine coordinates(xp , yp ). |
| Computation of projective coordinate system(X1,X2,Z1 and Z2) for MSB=1 |
| Assign initial values for X1,X2,Z1 and Z2. |
| Consider a point ‘P’ on the curve ‘C’ is xp=4; yp=3; |
| //initial values of LD algorithm |
| X1=1; Z1=0; |
| X2=xp; Z2=1; |
| Let T=Z1; |
| Z1=(X1*Z2+X2*Z1)^2; |
| X1=xp*Z1+X1*X2*T*Z2; |
| T=X2; |
| Z2=T^2*Z2^2; |
| b=1;//constant integer |
| X2=X2^4+b*Z2^4; |
| According LD algorithm, in the the first stage, three multiplications X1 Z2, X2 Z1, and T Z2 (T → X2) are performed in parallel by using three multipliers, and then three other multiplications x p Z1, X1X2T Z2 (T ← Z1), and bz2 4 are accomplished in parallel in the second stage, |
| Hence, the delay of each iteration is reduced from six field multiplication delays to two field multiplications delays. |
| Computation of projective coordinate system(X1,X2,Z1 and Z2) for MSB=0 |
| Assign initial values for X1,X2,Z1 and Z2. |
| Consider a point ‘P’ on the curve ‘C’ is xp=4; yp=3; |
| //initial values of LD algorithm |
| X1=1; Z1=0; |
| X2=xp; Z2=1; |
| Let T=Z2; |
| Z2=(X1*Z2+X2*Z1)^2; |
| X2=xp*Z2+X1*X2*T*Z1; |
| T=X1; |
| X1=X1^4+b*Z1^4; |
| Z1=T^2*Z1^2 |
| b=1;//constant integer |
| Flow of LD Algorithm: |
 |
 |
 |
References |
|