Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Further Results on Complementary Super Edge Magic Graph Labeling

Neelam Kumari1 and Seema Mehra2
 Department of Mathematics, M.D. University, Rohtak (Haryana), India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

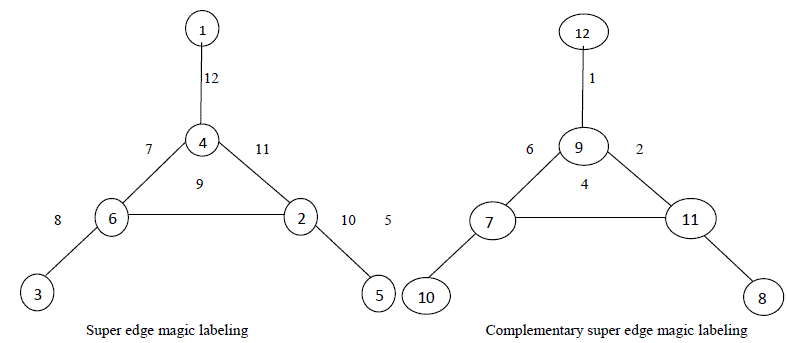
In this paper we introduced the concept of complementary super edge magic labeling and Complementary Super Edge Magic strength of a graph G.A graph G (V, E ) is said to be complementary super edge magic if there exist a bijection f:V U E → { 1, 2, …………p+q } such that p+q+1 - f(x) is constant. Such a labeling is called complementary super edge magic labeling with complementary super edge magic strength. In this paper for a graph G(V, E ) the complementary super edge magic labeling and minimum of all constants which is called complementary super edge magic strength of G is defined. In this paper, we investigate whether some families of graphs are complementary or not?

Keywords
Graph Labeling, Edge Magic Labeling ,Total Edge Magic Labeling, Super Edge Magic Labeling, Complementary Super Edge Magic Labeling .

INTRODUCTION
A labeling of a graph G is an assignment of mathematical objects to vertices , edges, or both vertices and edges subject to certain conditions. Graph labeling have applications in coding theory, networking addressing, and in many other fields. In most applications the labels are positive ( or nonnegative ) integers .In 1963 , Sedlack introduced a new class of labeling called magic labeling for a graph G (V, E ) , which is defined as a bijection f from E to a set of positive integers such that
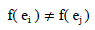image
image

MAIN RESULTS
In this paper the complementary super edge magic labeling and csems of two well known graphs such as the generalized prism Cm × Pn and G T ( n, n, n-1, n, 2n-1) are obtained. Before giving our main results we give a necessary and sufficient conditions for some graphs to have complementary super edge magic labeling.
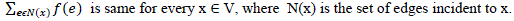image
image
image
Thus f is a super edge-magic of G with constant 15n, G and complementary super edge-magic labeling f is defined as for odd j,
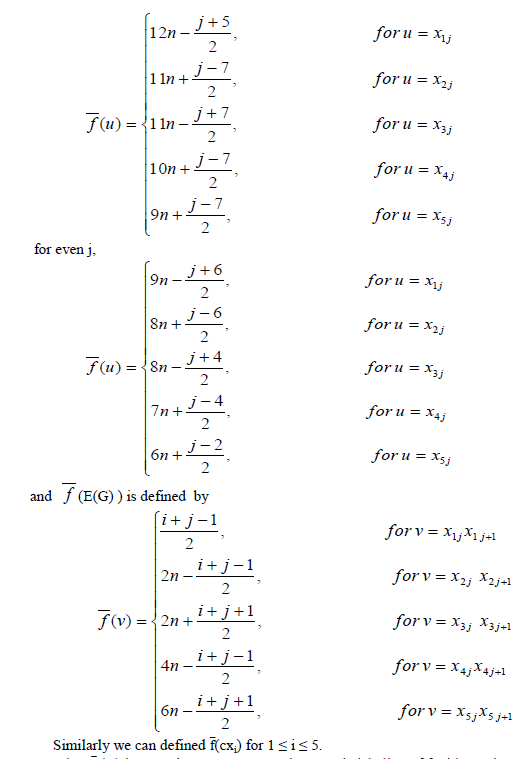image
Thus f (G) is complementary super edge -magic labeling of f with magic constant 21n-6 i.e. csems =21n-6. With this paper, we hope that interest in super edge-magic. and complementary super edgemagic labeling will aroused among those who study graph labeling.

References
  1. D. Craft and E. H Tesar On a question by Erdos about edge magic graph.Discrete Math. 207(1999)271-276
  2. G. Chartrand and L. Lesniak, Graphs and Digraphs,Wadsworth and Books/cole, Advanced Books and software Monterey , C.A(1986)
  3. H. Enomoto, A Llado, T. Nakamigawa and G. Ringel, Super edge magic graphs SUT J. Math. 34(1998)
  4. R.M Figueroa – Centeno, R. Ichishima and F. A Muntaner Batle, Enlarging the classes of edge magic 2 regular graphs, (pre-print)
  5. R. M. Figueroa Centeno, R Ichishima and F. A Muntaner- Batle, On edge magic labeling of certain disjoint unions of graphs, (pre-print)
  6. J. A Gallian, A dynamic survey of graph labeling, Electron J. Comb. S (2002) #D56
  7. R. D Godbold and P. Stater, All cycle are edge magic Bull Inst. Combin. Appl. 22(1998)93-97
  8. N.Harts field and G. Ringel, Pearls in Graph Theory, A comprehensive Introduction, Academic Press, San Diego, (1994)
  9. A. Kotzig and A. Rosa, Magic valuations of finite graphs, Canad Math. Bull. 13(1970)451-461
  10. A. Kotzig and A. Rosa, Magic valuations of complete graphs, Publications du Centre de Recherches Mathematiques Universite de Montreal, 175(19 72)
  11. G. Ringel and A Llado, Another tree conjecture, Bull. Inst. Combin. Appl. 18(1996)83-85
  12. W. D Wallis, Magic Graphs, Birkhauser Boston (2001)
  13. J.A.Gallian, Graph Labeling, Electron. J.Combin. 5(1998)(dynamic survey DS6
  14. R.M. Figueroa-Centeno, R.Ichishima, The place of super edge-magic labeling among other classes of labeling, Discrete Mathematics 231 (2001)153-168
  15. S. Roy and D.G. Akka, On Complementary edge magic of certain graphs, American Journal of Mathematics and Statistics 2012,2(3): 22-66.
  16. M.Baca, M.Murugan, Super edge- antimagic labeling of a cycle with a chord , Austral. J. Combin. 35 (2006), 253-261
  17. W. D Wallis, Magic Graphs, Birkhauser, Boston – Basel – Berlin, 2001.
  18. K.A.Sugeng, M.Miller and M. Baca , Super edge – antimagic total labeling s , Utilitas Math. 71 (2006), 131-141.
  19. Y. Roditty and T. Bachar , A note on edge magic cycles , Bull. Inst. Combin Appl. 29 (2000) , 94- 96.
  20. A. Semanicova , Graph Labelig , Ph. D. Thesis , P. J. Safarik University in Kosice , 2006.
  21. J.Ivanco , Z. Lastivkova and A. Semanicova, On magic and supermagic line graphs , Math. Bohemica 129 (2004), 33 – 42.
  22. R.M. Figueroa-Centeno, R.Ichishima, and F. A. Muntaner – Batle , On super edge magic graphs , Ars Combin. 64 (2002), 81-95
  23. E.T . Baskoro and A.A.G. Ngurah , On super edge magic total labeling of nP3 , Bull. Inst. Combin . Appl. 37 (2003), 82-87.