International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fused Data Structure for Tolerating Faults in Distributed System

Jeva Kumar M1, Golda Jeyasheeli P2
  1. PG Scholar, Dept of Computer Science Engineering, Mepco Schlenk, Engineering College, Sivakasi, India.
  2. Assistant Professor, Dept of Computer Science Engineering, Mepco Schlenk, Engineering College, Sivakasi, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

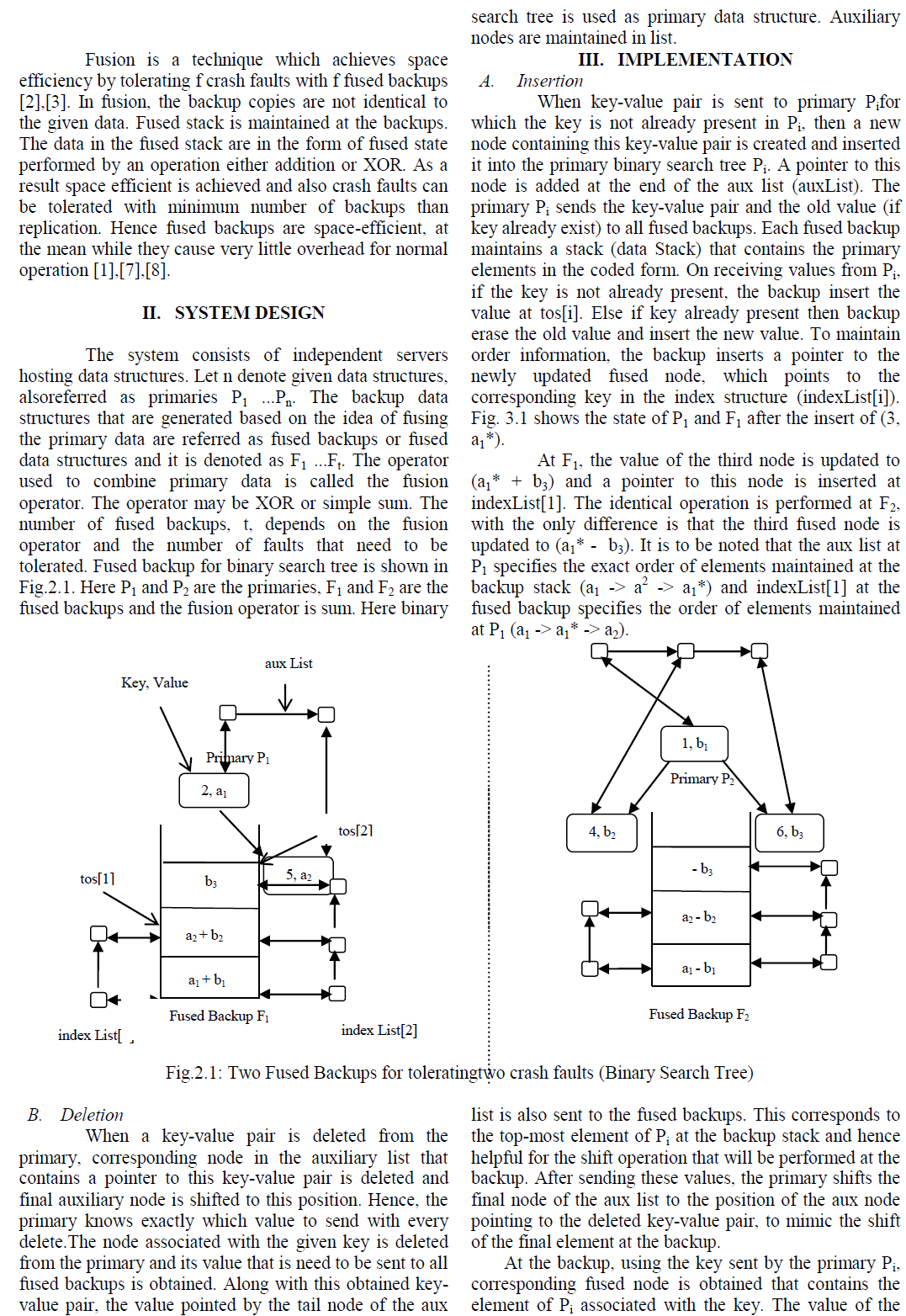
In Distributed systems, servers are prone to crash faults in which the data structures (queue, stack, etc) may crash, leading to a total loss in state. Hence it is necessary to tolerate crash faults in distributed system.Replication is the prevalent solution to tolerate crash faults .In replication, entire copy of the original data is taken and stored. Every update to original data reflects changes in the replicated data. Replication is used to ensure consistency, improve reliability, fault-tolerance and accessibility.To tolerate f crash faults among n distinct data structures, replication requires f replicas of each data structure, resulting in nf additional backups.Maintaining nf additional backups for n distinct data structures requires more space. In this project, fused data structure is used for backups which can tolerate f crash faults using just f additional fused backups.

Keywords
Distributed systems, fault tolerance, data structures.

INTRODUCTION
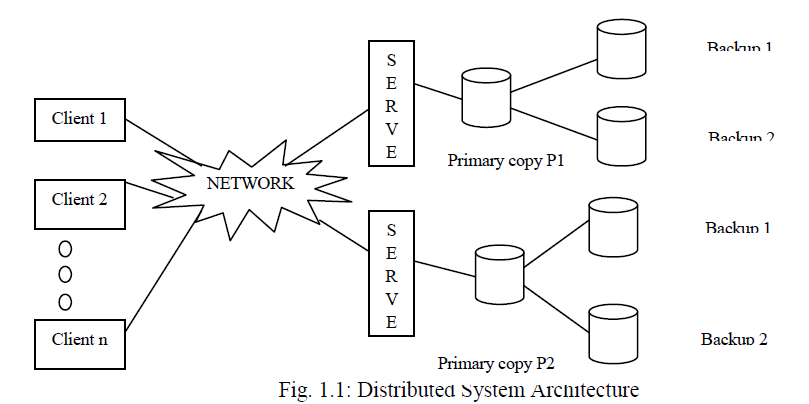
In distributed systems, servers maintain large instances of data structures such as linked lists, queues, and hash tables for handling list of pending request from theclients. These servers are prone to crash faults, leading to a total loss in state. Active replication [6],[7] is the mostly preferred solution. To tolerate f crash faults among n given data structures, replication maintains f + 1 replicas of each data structure, resulting in a total of nf backups. For example, consider a set of lock servers that maintain and coordinate the use of locks. Such a server maintains a list of pending requests in the form of a queue. To tolerate four crash faults among, say six independent lock servers each hosting a queue, replication requires four replicas of each queue, resulting in a total of 24 backup queues. For large values of n, this is expensive in terms of the space required by the backups as well as power and other resources to maintain the backup processes.Space efficient can be achieved by using Coding theory [4],[9].
image
image
image
image
f. Recovery Time
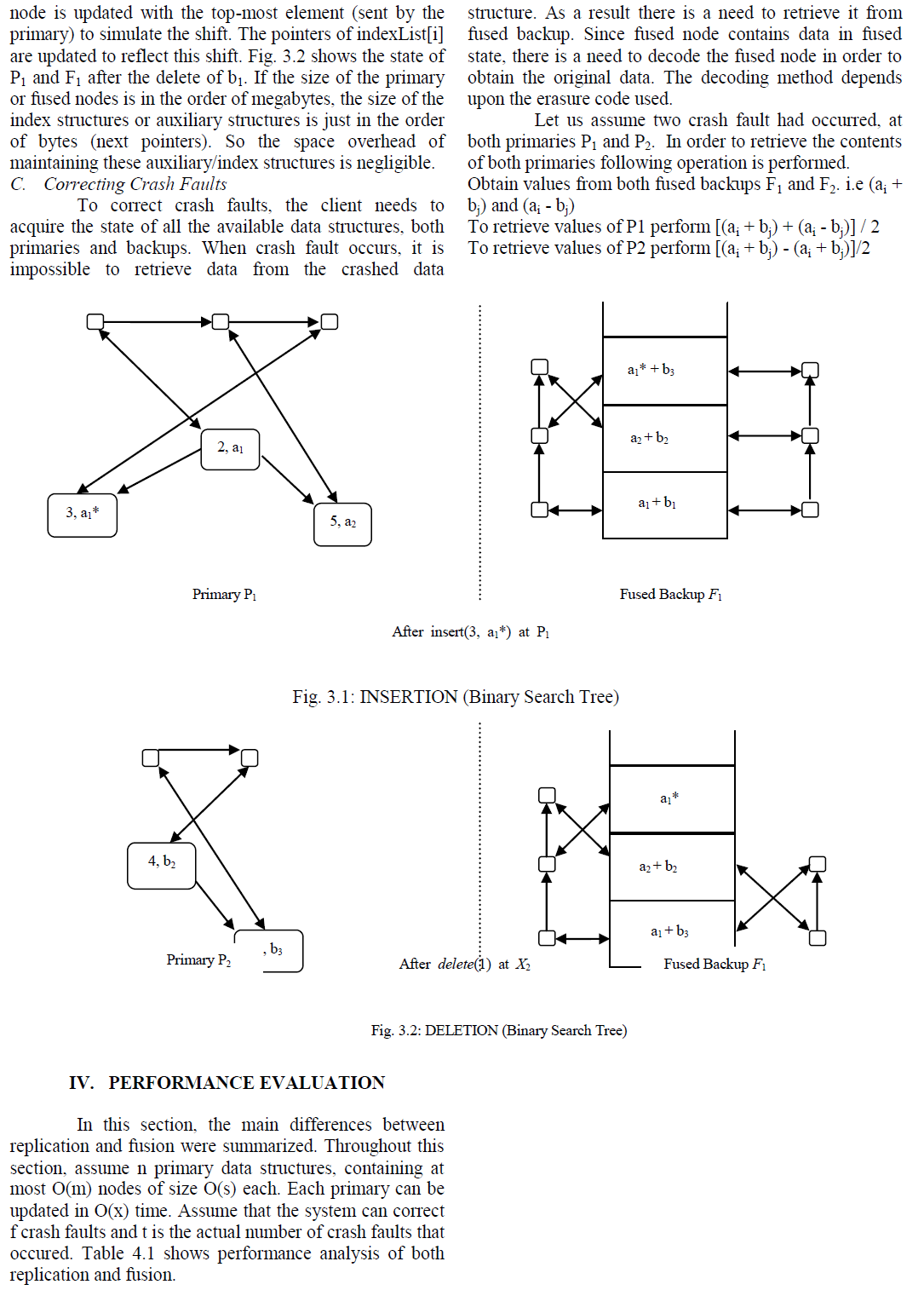
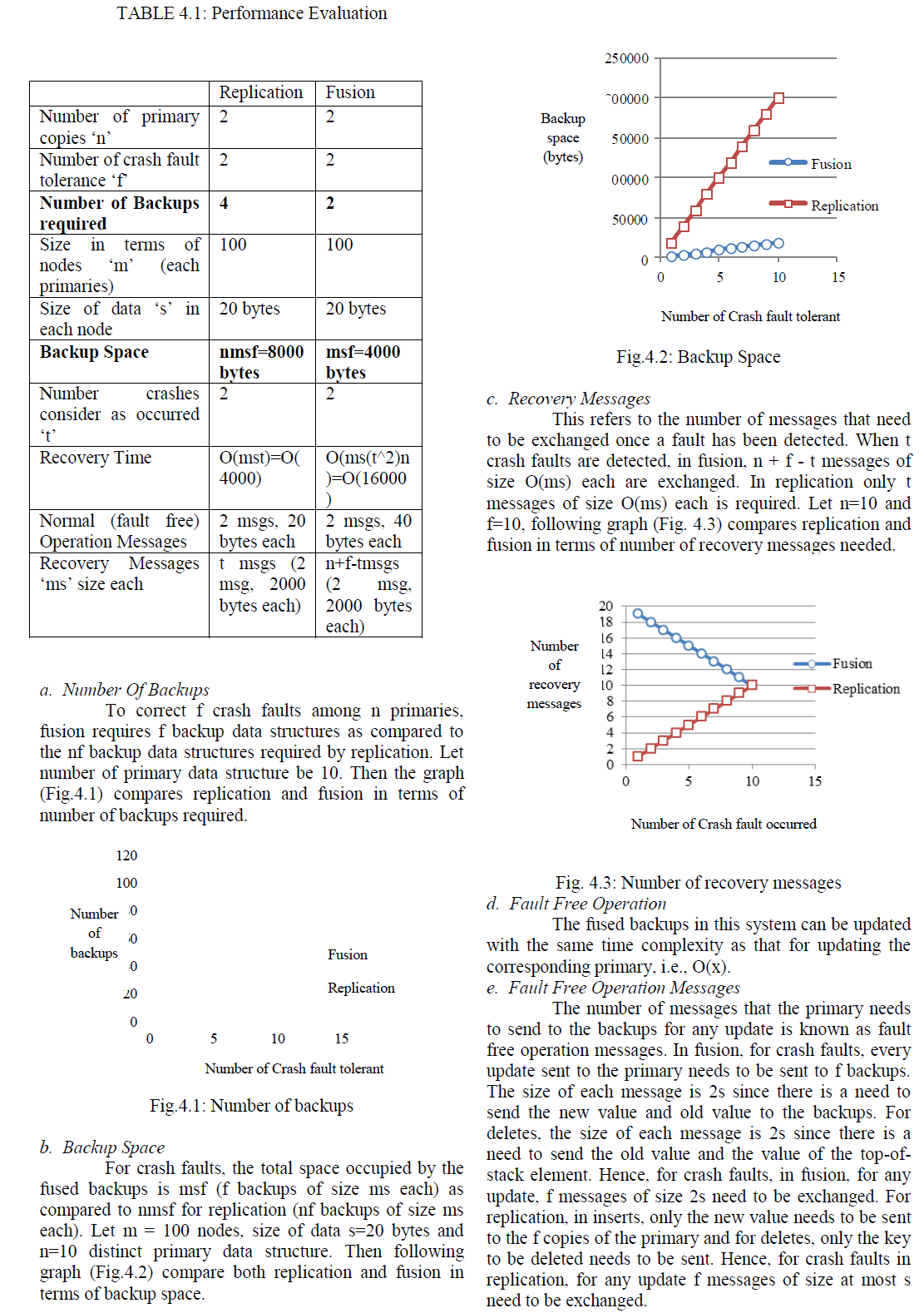
Recovery time is measured as the time taken to recover the state of the crashed data structures after the client obtains the state of the relevant data structures. In the case of fusion, to recover from t crash faults, there is a need to decode the backups with total time complexity O(mst2n). For replication, this is only O(mst). Thus, replication perform much better than fusion in terms of the time taken for recovery.
g. Update Time
Fusion has more update overhead as compared to replication. In fusion, the update time at a backup includes the time taken to locate the node to update plus the time taken to update the node‟s code value. The code update time was low and almost all the update time was spent in locating the node. Hence, optimizing the update algorithm can reduce the total update time.

CONCLUSION
Given n primaries, a fusion-based technique is presented for crash fault tolerance that guarantees O(n) savings in space as compared to replication with almost no overhead during fault free operation. Generic design of fused backups and their implementation for the data structures in the c++ that includes Linked List and Binary Search tree were provided. The main feature of this work is compared with replication. The performance result evaluation confirms that fusion is extremely space efficient while replication is efficient in terms of recovery and the size of the messages that need to be sent to the backups. Using the concepts presented in this project, there is a possibility for an alternate design using a combination of replication and fusion-based techniques. Thus here by conclude that fusion achieves significant savings in space, power, and other resources.

FUTURE WORK
This work can be extended to more number of data structure other than linked list and binary search tree.Update time in fused backup can be reduced by optimizing the update algorithm.Recovery time can be reduced by using efficient recovery algorithm.

References
  1. BharathBalasubramanian and Vijay K. GargG, “Fault Tolerance inDistributed Systems Using Fused Data Structures,” IEEE TransactionsOn Parallel And Distributed Systems, Vol. 24, No. 4, pg no. 701-715,April 2013.

  2. Balasubramanian B and V.K. Garg, “Fused Data Structure Library(Implemented in Java 1.6),” Parallel and Distributed SystemsLaboratory, http://maple.ece.utexas.edu, 2010.

  3. Balasubramanian B and V.K. Garg, “Fused Data Structures forHandling Multiple Faults in Distributed Systems,” Proc. Int‟l Conf.Distributed Computing Systems (ICDCS ‟11), pp. 677-688, June 201

  4. Berlekamp E.R, Algebraic Coding Theory. McGraw-Hill, 1968.

  5. Garg V.K and V. Ogale, “Fusible Data Structures for FaultTolerance,” Proc. 27th Int‟l Conf. Distributed Computing Systems(ICDCS ‟07), June 2007.

  6. HengmingZou, FarnamJahanian, “A Real-Time Primary-BackupReplication Service ”, IEEE Transactions On Parallel And DistributedSystems, Vol. 10, No. 6, Pg No. 533-548, June 1999.

  7. Maria Chtepen, Filip H.A. Claeys, Bart hoedt, Filip De Turck, Piet Demeester , Peter A. Vanrolleghem , “Adaptive Task Checkpointing and Replication: Toward Efficient Fault-Tolerant Grids ”, IEEE Transactions On Parallel And Distributed Systems, Vol. 20, No. 2, Pg No. 180-190, February 2009 .

  8. Ogale V, B. Balasubramanian, and V.K. Garg, “A Fusion-Based Approach for Tolerating Faults in Finite State Machines,” Proc. IEEE Int‟l Symp. Parallel and Distributed Processing (IPDPS ‟09), pp. 1-11, 2009.

  9. W.W. Peterson and E.J. Weldon, Error-Correcting Codes - Revised, second ed. The MIT Press, Mar. 1972.