International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fuzzy Pairwise Strongly Pre-Continuous Mappings

Madhulika Shukla
Associate professor, Department of Applied Mathematics, GGITS Engineering College, Jabalpur (M.P.) India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

We define and characterize a fuzzy pairwise strongly pre-continuous mappings on a fuzzy bitopological space. We investigate some of their properties. We establish some equivalent conditions of fuzzy pairwise strongly precontinuous mappings on a fuzzy bitopological space.

Keywords
(τi, τj)-fuzzy preopen, (τi, τj)-fuzzy preclosed, (τi, τj)-fuzzy semi-open, (τi, τj)-fuzzy semi-closed, (τi, τj)- fuzzy pairwise precontinuous, (τi, τj) -fuzzy pairwise semicontinuous, (τi, τj) -fuzzy pairwise stongly pre-continuous, (τi, τj)-fuzzy pairwise strongly preclosed.

INTRODUCTION
In 1981, K.K. Azad [4] introduced the concept of semi-open sets in fuzzy topology. A.S. Bin Shahana [1] has defined the concept of fuzzy pre-open sets in fuzzy topological spaces.
In 1989, A. Kandil [5] introduced the notation of fuzzy bitopological space. Further in 1996, S.S. Thakur and R. Malviya [9] defined fuzzy semi-open and fuzzy semi-continuous in fuzzy bitopological space. Sampath kumar [10] defined a (τi, τj)-fuzzy pre-open set and characterized a fuzzy pairwise precontinuous mappings on a fuzzy bitopological space. Further M. Shrivastava, J.K.m maitra And M. Shukla [7] in 2006 defined fuzzy strongly pre-continuous mapping in fuzzy topological space
In this article we have established equivalent conditions for a mapping to be fuzzy pairwise strongly pre-continuous mapping in fuzzy bitopological space. Further we have studied some properties of fuzzy pairwise pre-continuous mapping.

PRELIMINARIES
image
image

FUZZY PAIRWISE STRONGLY PRE-CONTINUOUS MAPPINGS
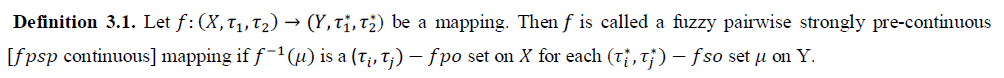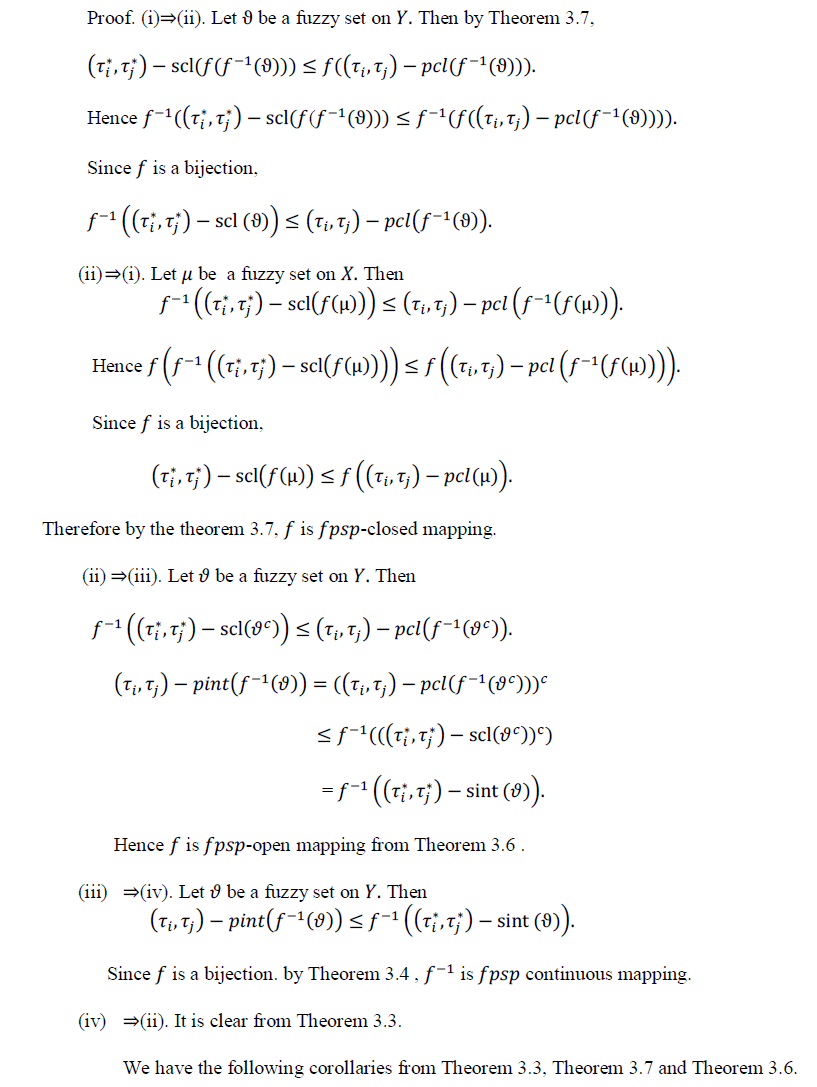image
image
image
image
image
`image

Concluding remark:
1. We have introduced and studied new kind of map fuzzy pairwise Strongly pr-econtinuos maps on fuzzy bitopological spaces.
2. We defined the relation between fuzzy pairwise pre continuous and fuzzy pairwise strongly continuous map. We investigated some of their properties.
3. We proved that the fuzzy pairwise storgly pre-continuous map is stronger form of fuzzy paqairwise pre-continuous map by use of example.
4. We have established some significant properties of fuzzy pairwise strogly pre-continuous maps.
5. We introduce and study new kind of fuzzy pairwise strongly pre-closed and investigate of their properties.

References
  1. A. S. Bin Shahana, On fuzzy strong semi-continuity and fuzzy pre continuity, Fuzzy Sets and Systems, 44 (1991), 303-308.
  2. C. L. Chang ., Fuzzy topological spaces. J. Math. Anal. Appl. 24 (1968), 182-190.
  3. H.S. Lee, J.S. Lee and Y.B. Im, Fuzzy pairwise strong pre-irresolute continuous mappings. J. Appl. Math & Informatics. 28(2010), 1561-1571.
  4. K.K. Azad ., On fuzzy semi continuity, fuzzy almost continuity and fuzzy weak continuity. J. Math. Anal. Appl. 82 (1981), 14-32.
  5. Kandil, Biproximities and fuzzy bitopological spaces, Simon Stevin. 63(1989) 45-66.
  6. L. A. Zadeh , Fuzzy Sets, Inform. And control, 8 (1965), 338-353.
  7. M. Shrivastava . J.K. Maitra J.K. and M. Shukla., On fuzzy strongly pre continuous mappings, VISLESANA, 10-B (2) (2006), 109-117.
  8. M. Shukla , Fuzzy pairwise strongly continuois mapping in J. Comp. & Maths. Sci. Vol. 3, No.6, (2012), pp 631-636.
  9. S. S. Thakur and R. Malviya., Semi-open sets and semi-continuity in fuzzy bitopological spaces. Fuzzy Sets and Systems. 79 (1996) 251-256.
  10. S. Sampath kumar . On fuzzy pairwise continuous and fuzzy pairwise pre-continuity. Fuzzy Sets and Systems. 62 (1994), 231-238.