Generalized PreSemi Continuous and Irresolute Mappings in Intuitionistic Fuzzy Topological Space

Abstract

In this paper, we introduce and study the notions of intuitionistic fuzzy generalized presemi continuous mappings and intuitionistic fuzzy generalized presemi irresolute mappings and study some of its properties in intuitionistic fuzzy topological spaces.

Keywords

Intuitionistic fuzzy topology, Intuitionistic fuzzy point, Intuitionistic fuzzy generalized presemi closed sets, Intuitionistic fuzzy generalized presemi continuous mappings and Intuitionistic fuzzy generalized presemi irresolute mappings.

2010 Mathematics Subject Classification: 54A40, 03F55.

INTRODUCTION

The concept of fuzzy set [FS] was introduced by Zadeh [15] and later fuzzy topology was introduced by Chang [2] in 1967. By adding the degree of non membership to FS, Atanassov [1] proposed intuitionistic fuzzy set [IFS] using the notion of fuzzy sets. On the other hand Coker [3] introduced intuitionistic fuzzy topological spaces using the notion of intuitionistic fuzzy sets. In this paper we introduce intuitionistic fuzzy generalized presemi continuous mappings and intuitionistic fuzzy generalized presemi irresolute mappings and study some of their basic properties.

PRELIMINARIES

Throughout this paper, (X, τ) or X denotes the intuitionistic fuzzy topological spaces (briefly IFTS). For a subset A of X, the closure, the interior and the complement of A are denoted by cl(A), int(A) and Ac respectively. We recall some basic definitions that are used in the sequel.

Definition 2.1: [1] Let X be a non-empty fixed set. An intuitionistic fuzzy set (IFS in short) A in X is an object having the form A = {⟨x, μA(x), νA(x)⟩/ x ∈ X} where the functions μA : X → [0,1] and νA : X → [0,1] denote the degree of membership (namely μA(x)) and the degree of nonmembership (namely νA(x)) of each element x ∈ X to the set A, respectively, and 0 ≤ μA(x) + νA(x) ≤ 1 for each x ∈ X. Denote by IFS(X), the set of all intuitionistic fuzzy sets in X.

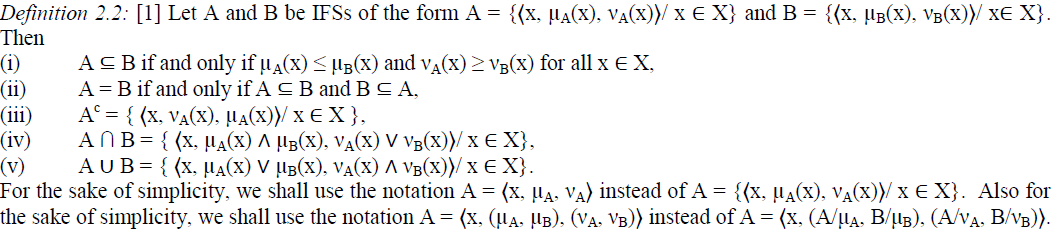An IFS A of an IFTS (X, τ) is called an intuitionistic fuzzy generalized pre regular open set and intuitionistic fuzzy generalized pre open set (IFGPROS and IFGPOS for short) if the complement Ac is an IFGPRCS and IFGPCS respectively.

Definition 2.11: [9] An IFS A is an IFTS (X, τ) is said to be an intuitionistic fuzzy generalized semipre closed set (IFGSPCS for short) if spcl(A) ⊆ U whenever A ⊆ U and U is an IFOS in (X, τ). An IFS A of an IFTS (X, τ) is called an intuitionistic fuzzy generalized semipre open set (IFGSPOS for short) if Ac is an IFGSPCS in (X, τ).

Definition 2.12: [8] An IFS A in an IFTS (X, τ) is said to be an intuitionistic fuzzy generalized presemi closed set (IFGPSCS for short) if pcl(A) ⊆ U whenever A ⊆ U and U is an IFSOS in (X, τ). The family of all IFGPSCSs of an IFTS (X, τ) is denoted by IFGPSC(X). Every IFCS, IFRCS, IFαCS, IFPCS, IFWCS are an IFGPSCS and every IFGPSCS is an IFGPCS, IFGPRCS, IFGSPCS, IFGSPRCS but the converses are not true in general.

Definition 2.13: [8] The complement Ac of an IFGPSCS A in an IFTS (X, τ) is called an intuitionistic fuzzy generalized presemi open set (IFGPSOS for short) in X. Every IFOS, IFROS, IFαOS, IFPOS, IFWOS are an IFGPSOS and every IFGPSOS is an IFGPOS, IFGPROS, IFGSPOS, IFGSPROS but the converses are not true in general.

Definition 2.14: [6] An IFS A in an IFTS (X, τ) is said to be an intuitionistic fuzzy generalized semipre regular closed set (IFGSPRCS for short) if spcl(A) ⊆ U whenever A ⊆ U and U is an IFROS in (X, τ). Definition 2.15: [6] The complement Ac of an IFGSPRCS A in an IFTS (X, τ) is called an intuitionistic fuzzy generalized semipre regular open set (IFGSPROS for short) in X.

Definition 2.16: [11] Let α, β ∈ [0, 1] and α + β ≤ 1. An intuitionistic fuzzy point (IFP for short) p(α, β) of X is an IFS of X defined by

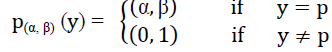Definition 2.17: [8] If every IFGPSCS in (X, τ) is an IFPCS in (X, τ), then the space can be called as an intuitionistic fuzzy presemi T1/2 (IFPST1/2 for short) space.

Definition 2.18: [4] Let f be a mapping from an IFTS (X, τ) into an IFTS (Y, σ). Then f is said to be intuitionistic fuzzy continuous (IF continuous for short) if f -1(B) ∈ IFO(X) for every B ∈ σ.

Definition 2.19: [4] Let f be a mapping from an IFTS (X, τ) into an IFTS (Y, σ). Then f is said to be

(i) intuitionistic fuzzy α- continuous(IFα continuous for short) if f -1(B) ∈ IFαO(X) for every B ∈ σ,

(ii) intuitionistic fuzzy pre continuous(IFP continuous for short) if f -1(B) ∈ IFPO(X) for every B ∈ σ.

Definition 2.20: [12] A mapping f: (X, τ) → (Y, σ) is called an intuitionistic fuzzy weakly continuous (IFW continuous for short) mappings if f -1(V) is an IFWCS in (X, τ) for every IFCS V of (Y, σ). Definition 2.21: [13] A mapping f: (X, τ) → (Y, σ) is called an intuitionistic fuzzy generalized pre regular continuous (IFGPR continuous for short) mappings if f -1(V) is an IFGPRCS in (X, τ) for every IFCS V of (Y, σ).

Definition 2.22: [10] A mapping f: (X, τ) →(Y, σ) is called an intuitionistic fuzzy generalized semipre continuous (IFGSP continuous for short) mapping if f -1(V) is an IFGSPCS in (X, τ) for every IFCS V of (Y, σ). Definition 2.23: [7] A mapping f: (X, τ) →(Y, σ) is called an intuitionistic fuzzy generalized semipre regular continuous (IFGSPR continuous for short) mapping if f -1(V) is an IFGSPRCS in (X, τ) for every IFCS V of (Y, σ).

Result 2.24: [8] For any IFS A in (X, τ) where X is an IFPST1/2 space, A ∈ IFGPSO(X) if and only if for every IFP p(α, β) ∈ A, there exists an IFGPSOS B in X such that p(α, β) ∈ B ⊆ A.

INTUITIONISTIC FUZZY GENERALIZED PRESEMI CONTINUOUS MAPPINGS

In this section we have introduce intuitionistic fuzzy generalized presemi continuous mapping and investigate some of its properties in intuitionistic fuzzy topological spaces.

Definition 3.1: A mapping f: (X, τ) → (Y, σ) is called an intuitionistic fuzzy generalized presemi continuous (IFGPS continuous for short) mappings if f -1(V) is an IFGPSCS in (X, τ) for every IFCS V of (Y, σ). For the sake of simplicity, we shall use the notation A= ⟨x, (μ, μ), (ν, ν)⟩ instead of A= ⟨x, (a/μa, b/μb), (a/νa, b/νb)⟩ in all the examples used in this paper. Example 3.2: Let X= {a, b}, Y= {u, v} and G1 = ⟨x, (0.5, 0.4), (0.5, 0.6)⟩, G2 = ⟨y, (0.6, 0.7), (0.4, 0.2)⟩. Then τ = {0~, G1, 1~} and σ = {0~, G2, 1~} are IFTs on X and Y respectively. Define a mapping f: (X, τ) → (Y, σ) by f(a) = u and f(b) = v. Then f is an IFGPS continuous mapping.

Theorem 3.3: Every IF continuous mapping is an IFGPS continuous mapping but not conversely.

Proof: Let f: (X, τ) → (Y, σ) be an IF continuous mapping. Let V be an IFCS in Y. Then f -1(V) is an IFCS in X. Since every IFCS is an IFGPSCS, f -1(V) is an IFGPSCS in X. Hence f is an IFGPS continuous mapping.

Example 3.4: In Example 3.2, f: (X, τ) → (Y, σ) is an IFGPS continuous mapping but not an IF continuous mapping. Since G2 = ⟨y, (0.6, 0.7), (0.4, 0.2)⟩ is an IFOS in Y but f -1(G2) = ⟨x, (0.6, 0.7), (0.4, 0.2)⟩ is not an IFOS in X. Theorem 3.5: Every IFα continuous mapping is an IFGPS continuous mapping but not conversely. Proof: Let f: (X, τ) → (Y, σ) be an IFα continuous mapping. Let V be an IFCS in Y. Then f -1(V) is an IFαCS in X. Since every IFαCS is an IFGPSCS, f -1(V) is an IFGPSCS in X. Hence f is an IFGPS continuous mapping. Example 3.6: In Example 3.2, f: (X, τ) → (Y, σ) is an IFGPS continuous mapping but not an IFα continuous mapping. Since G2 = ⟨y, (0.6, 0.7), (0.4, 0.2)⟩ is an IFOS in Y but f -1(G2) = ⟨x, (0.6, 0.7), (0.4, 0.2)⟩ is not an IFαOS in X. Theorem 3.7: Every IFP continuous mapping is an IFGPS continuous mapping but not conversely. Proof: Let f: (X, τ) → (Y, σ) be an IFP continuous mapping. Let V be an IFCS in Y. Then f -1(V) is an IFPCS in X. Since every IFPCS is an IFGPSCS, f -1(V) is an IFGPSCS in X. Hence f is an IFGPS continuous mapping. Example 3.8: Let X = {a, b}, Y = {u, v} and G1 = ⟨x, (0.2, 0.1), (0.8, 0.9)⟩, G2 = ⟨x, (0.5, 0.6), (0.5, 0.4)⟩, G3 = ⟨y, (0.1, 0.4), (0.9, 0.6)⟩. Then τ = {0~, G1, G2, 1~} and σ = {0~, G3, 1~} are IFTs on X and Y respectively. Define a mapping f: (X, τ) → (Y, σ) by f(a) = u and f(b) = v. Then f is an IFGPS continuous mapping but not an IFP continuous mapping.

Theorem 3.9: Every IFW continuous mapping is an IFGPS continuous mapping but not conversely.

Proof: Let f: (X, τ) → (Y, σ) be an IFW continuous mapping. Let V be an IFCS in Y. Then f -1(V) is an IFWCS in X. Since every IFWCS is an IFGPSCS, f -1(V) is an IFGPSCS in X. Hence f is an IFGPS continuous mapping.

Example 3.10: In Example 3.2, f: (X, τ) → (Y, σ) is an IFGPS continuous mapping but not an IFW continuous mapping. Since G2 = ⟨y, (0.6, 0.7), (0.4, 0.2)⟩ is an IFOS in Y but f -1(G2) = ⟨x, (0.6, 0.7), (0.4, 0.2)⟩ is not an IFWOS in X.

Theorem 3.11: Every IFGPS continuous mapping is an IFGPR continuous mapping but not conversely.

Proof: Let f: (X, τ) → (Y, σ) be an IFGPS continuous mapping. Let V be an IFCS in Y. Then f -1(V) is an IFGPSCS in X. Since every IFGPSCS is an IFGPRCS, f -1(V) is an IFGPRCS in X. Hence f is an IFGPR continuous mapping. Example 3.12: Let X = {a, b}, Y = {u, v} and G1 = ⟨x, (0.3, 0.2), (0.7, 0.8)⟩, G2 = ⟨y, (0.5, 0.6), (0.5, 0.4)⟩. Then τ = {0~, G1, 1~} and σ = {0~, G2, 1~} are IFTs on X and Y respectively. Define a mapping f: (X, τ) → (Y, σ) by f(a) = u and f(b) = v. Then f is an IFGPR continuous mapping but not an IFGPS continuous mapping. Theorem 3.13: Every IFGPS continuous mapping is an IFGSP continuous mapping but not conversely.

Proof: Let f: (X, τ) → (Y, σ) be an IFGPS continuous mapping. Let V be an IFCS in Y. Then f -1(V) is an IFGPSCS in X. Since every IFGPSCS is an IFGSPCS, f -1(V) is an IFGSPCS in X. Hence f is an IFGSP continuous mapping. Example 3.14: In Example 3.12, f: (X, τ) → (Y, σ) is an IFGSP continuous mapping but not an IFGPS continuous mapping. Theorem 3.15: Every IFGPS continuous mapping is an IFGSPR continuous mapping but not conversely. Proof: Let f: (X, τ) → (Y, σ) be an IFGPS continuous mapping. Let V be an IFCS in Y. Then f -1(V) is an IFGPSCS in X. Since every IFGPSCS is an IFGSPRCS, f -1(V) is an IFGSPRCS in X. Hence f is an IFGSPR continuous mapping.

Example 3.16: In Example 3.12, f: (X, τ) → (Y, σ) is an IFGSPR continuous mapping but not an IFGPS continuous mapping.

Theorem 3.17: Let f: (X, τ) → (Y, σ) be a mapping where f -1(V) is an IFRCS in X for every IFCS in Y. Then f is an IFGPS continuous mapping but not conversely.

Proof: Let A be an IFCS in Y. Then f -1(V) is an IFRCS in X. Since every IFRCS is an IFGPSCS, f -1(V) is an IFGPSCS in X. Hence f is an IFGPS continuous mapping.

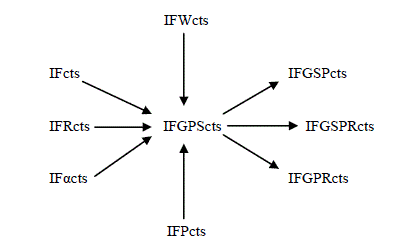
Example 3.18: In Example 3.2, f: (X, τ) → (Y, σ) is an IFGPS continuous mapping but not a mapping defined in Theorem 3.17. The relation between various types of intuitionistic fuzzy continuity is given in the following diagram. In this diagram „cts‟ means continuous.

Theorem 3.19: If f: (X, τ) → (Y, σ) is an IFGPS continuous mapping, then for each IFP p(α, β) of X and each A ∈ σ such that f(p(α, β)) ∈ A. Then there exists an IFGPSOS B of X such that p(α, β) ∈ B and f(B) ⊆ A.

Proof: Let p(α, β) be an IFP of X and A ∈ σ such that f(p(α, β)) ∈ A. Put B = f -1(A). Then by hypothesis B is an IFGPSOS in X such that p(α, β) ∈ B and f(B) = f(f -1(A)) ⊆ A.

Theorem 3.20: Let f: (X, τ) → (Y, σ) be an IFGPS continuous mapping. Then f is an IFP continuous mapping if X is an IFPST1/2 space. Proof: Let V be an IFCS in Y. Then f -1(V) is an IFGPSCS in X, by hypothesis. Since X is an IFPST1/2 space, f -1(V) is an IFPCS in X. Hence f is an IFP continuous mapping. Theorem 3.21: Let f: (X, τ) → (Y, σ) be an IFGPS continuous mapping and g: (Y, σ) → (Z,η) is an IF continuous mapping, then g ∘ f: (X, τ) →(Z,η) is an IFGPS continuous mapping. Proof: Let V be an IFCS in Z. Then g -1(V) is an IFCS in Y, by hypothesis. Since f is an IFGPS continuous mapping, f -1(g -1(V)) is an IFGPSCS in X. Hence g ∘ f is an IFGPS continuous mapping.

Theorem 3.22: Let f: (X, τ) → (Y, σ) be a mapping from an IFTS X into an IFTS Y. Then the following conditions are equivalent if X and Y are IFPST1/2 space:

(i) f is an IFGPS continuous mapping,

(ii) f -1(B) is an IFGPSOS in X for each IFOS B in Y,

(iii) for every IFP p(α, β) in X and for every IFOS B in Y such that f(p(α, β)) ∈ B, there exists an IFGPSOS A in X such that p(α, β) ∈ A and f(A) ⊆ B.

Proof: (i) ⟺ (ii) is obvious, since f -1(Ac) = (f -1(A))c. (ii) ⇒ (iii) Let B be any IFOS in Y and let p(α, β) ∈ X. Given f(p(α, β)) ∈ B. By hypothesis f -1(B) is an IFGPSOS in X. Take A = f -1(B). Now p(α, β) ∈ f -1(f(p(α, β)). Therefore f -1(f(p(α, β)) ∈ f -1(B) = A. This implies p(α, β) ∈ A and f(A) = f(f -1(B)) ⊆ B. (iii) ⇒ (i) Let A be an IFCS in Y. Then its complement, say B = Ac, is an IFOS in Y. Let p(α, β) ∈ C and f(C) ⊆ B. Now C ⊆ f -1(f(C)) ⊆ f -1(B). Thus p(α, β) ∈ f -1(B). Therefore f -1(B) is an IFGPSOS in X by Result 2.24. That is f -1(Ac) is an IFGPSOS in X and hence f -1(A) is an IFGPSCS in X. Thus f is an IFGPS continuous mapping.

INTUITIONISTIC FUZZY GENERALIZED PRESEMI IRRESOLUTE MAPPINGS

In this section we have introduced intuitionistic fuzzy generalized presemi irresolute mappings and studied some of their properties.

Definition 4.1: A mapping f: (X, τ) → (Y, σ) be an intuitionistic fuzzy generalized presemi irresolute (IFGPS irresolute) mapping if f -1(V) is an IFGPSCS in (X, τ) for every IFGPSCS V of (Y, σ).

Theorem 4.2: Let f: (X, τ) → (Y, σ) and g: (Y, σ) → (Z, γ) be IFGPS irresolute mapping. Then g ∘ f: (X, τ) → (Z, γ) is an IFGPS irresolute mapping.

Proof: Let V be an IFGPSCS in Z. Then g -1(V) is an IFGPSCS in Y. Since f is an IFGPS irresolute, f-1(g -1(V)) is an IFGPSCS in X, by hypothesis. Hence g ∘ f is an IFGPS irresolute mapping.

Theorem 4.3: Let f: (X, τ) → (Y, σ) be an IFGPS irresolute mapping and g: (Y, σ) → (Z, γ) be IFGPS continuous mapping, the g ∘ f: (X, τ) → (Z, γ) is an IFGPS continuous mapping.

Proof: Let V be an IFCS in Z. Then g -1(V) is an IFGPSCS in Y. Since f is an IFGPS irresolute mapping, f -1(g -1(V)) is an IFGPSCS in X. Hence g ∘ f is an IFGPS continuous mapping.

Theorem 4.4: Let f: (X, τ) → (Y, σ) be a mapping from an IFTS X into an IFTS Y. Then the following conditions are equivalent if X and Y are IFPST1/2 space:

(i) f is an IFGPS irresolute mapping,

(ii) f -1(B) is an IFGPSOS in X for each IFGPSOS B in Y,

(iii) f -1(pint(B)) ⊆ pint(f -1(B)) for each IFS B of Y,

(iv) pcl(f -1(B)) ⊆ f -1(pcl(B)) for each IFS B of Y.

Proof: (i) ⟺ (ii) is obvious, since f -1(Ac) = (f -1(A))c. (ii) ⇒ (iii) Let B be any IFS in Y and pint(B) ⊆ B. Also f -1(pint(B)) ⊆ f -1(B). Since pint(B) is an IFPOS in Y, it is an IFGPSOS in Y. Therefore f -1(pint(B)) is an IFGPSOS in X, by hypothesis. Since X is an IFPST1/2 space, f -1(pint(B)) is an IFPOS in X. Hence f -1(pint(B)) = pint(f-1(pint(B))) ⊆ pint(f -1(B)). (iii) ⇒ (iv) is obvious by taking complement in (iii). (iv) ⇒ (i) Let B be an IFGPSCS in Y. Since Y is an IFPST1/2 space, B is an IFPCS in Y and pcl(B) = B. Hence f -1(B) = f -1(pcl(B)) ⊇ pcl(f -1(B)), by hypothesis. But f -1(B) ⊆ pcl(f -1(B)). Therefore pcl(f -1(B)) = f -1(B). This implies f -1(B) is an IFPCS and hence it is an IFGPSCS in X. Thus f is an IFGPS irresolute mapping.

Theorem 4.5: Let f: (X, τ) → (Y, σ) be an IFGPS irresolute mapping from an IFTS X into an IFTS Y. Then f -1(B) ⊆ pint(f -1(int(cl(B)))) for every IFGPSOS B in Y, if X and Y are IFPST1/2 spaces.

Proof: Let B be an IFGPSOS in Y. Then by hypothesis f -1(B) is an IFGPSOS in X. Since X is an IFPST1/2 space, f -1(B) is an IFPOS in X. Therefore pint(f -1(B)) = f -1(B). Since Y is an IFPST1/2 space, B is an IFPOS in Y and B ⊆ int(cl(B)). Now f -1(B) = pint(f -1(B)) implies, f -1(B) ⊆ pint(f -1(int(cl(B))).

Theorem 4.6: Let f: (X, τ) → (Y, σ) be an IFGPS irresolute mapping from an IFTS X into an IFTS Y. Then f -1(B) ⊆ pint(int(cl(f -1(B)))) for every IFGPSOS B in Y, if X and Y are IFPST1/2 spaces.

Proof: Let B be an IFGPSOS in Y. Then by hypothesis f -1(B) is an IFGPSOS in X. Since X is an IFPST1/2 space, f -1(B) is an IFPOS in X. Therefore pint(f -1(B)) = f -1(B) ⊆ int(cl(f -1(B))). Hence f -1(B) ⊆ pint(int(cl(f -1(B)))).

References

1. Atanassov, K., "Intuitionistic fuzzy sets", Fuzzy Sets and Systems, 20, 87-96, 1986.
2. Chang, C. L., "Fuzzy topological spaces", J. Math. Anal. Appl. 24, 182-190, 1968.
3. Coker, D., "An introduction to intuitionistic fuzzy topological space", Fuzzy Sets and Systems, 88, 81-89, 1997.
4. Gurcay, H., Haydar, Es. A., and Coker, D.,"On fuzzy continuity in intuitionistic fuzzy topological spaces", J.Fuzzy Math.5 (2), 365-378, 1997.
5. Rajarajeswari, P., and Senthil Kumar, L.," Generalized pre-closed sets in intuitionistic fuzzy topological spaces", International journal of Fuzzy Mathematics and Systems, 3, 253–262, 2011.
6. Ramesh, K., and Thirumalaiswamy, M., "Generalized semipre regular closed sets in intuitionistic fuzzy topological spaces," International Journal of Computer Applications Technology and Research, Vol. 2, Issue 3, 324 - 328, 2013.
7. Ramesh, K., and Thirumalaiswamy, M., "Generalized semipre regular continuous and irresolute mappings in intuitionistic fuzzy topological spaces, International Journal of Engineering Research & Technology, Vol. 2 Issue 8, 832-838, 2013.
8. Sampoornam, T., Gnanambal Ilango and Ramesh, K., "Generalized presemi closed sets in intuitionistic fuzzy topological spaces”,(Submitted).
9. Santhi, R., and Jayanthi, D., "Intuitionistic fuzzy generalized semipre closed sets," Tripura Math.Soci., 61-72, 2009.
10. Santhi, R., and Jayanthi, D., "Intuitionistic Fuzzy Generalized Semi-Pre Continuous Mappings", Int. J. Contemp. Math. Sciences, Vol. 5, no. 30, 1455 – 1469, 2010.
11. Seok Jong Lee and Eun Pyo Lee, "The category of intuitionistic fuzzy topological spaces", Bull. Korean Math. Soc. 37, No. 1, pp. 63-76, 2000.
12. Thakur, S. S., Jyoti Pandey Bajpai, “Intuitionistic Fuzzy w-closed sets and intuitionistic fuzzy w-continuity”, International Journal of Contemporary Advanced Mathematics, Vol. 1, No. 1, 1–1, 2010.
13. Thakur, S. S., and Jyoti Pandey Bajpai, "On intuitionistic fuzzy Gpr-closed sets", Fuzzy Inf. Eng, 4: 425-444, 2012.
14. Young Bae Jun and Seok-Zun Song," Intuitionistic fuzzy semipre open sets and Intuitionistic fuzzy semi-pre continuous mappings", Jour. of Appl. Math & computing, 467-474, 2005.
15. Zadeh, L. A.," Fuzzy sets", Information and control, 8, 338-353, 1965.