ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Shreen Sumayya A G1, Rajakumari K2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
With the wide deployment of public cloud computing infrastructures, using clouds to host data query services has become an appealing solution for the advantages on scalability and cost-saving. However, some data might be sensitive that the data owner does not want to move to the cloud unless the data confidentiality and query privacy are guaranteed. Due to diversity of applications, the database services in cloud must also support storage of multidimensional data. On the other hand, a secured query service should still provide efficient query processing and significantly reduce the in-house workload to fully realize the benefits of cloud computing. The base paper propose the RASP data perturbation method to provide secure and efficient range query and kNN query services for protected data in the cloud [1]. The kNN-R algorithm is designed to work with the RASP range query algorithm to process the kNN queries. But kNN-R algorithm will not work effectively in high dimensional data (complex objects such as spatial, temporal and multimedia data). In this paper, we integrate kNN-R algorithm and the traditional concept of R-optimality and propose a new multi-step RI kNN-R search algorithm that utilizes lower- and upper bounding distance information (Ilu) in the filter step.In order to reduce the number of candidates returned from the filter step which then have to be exactly evaluated in the refinement step is fundamental for the efficiency of the query process.
Keywords |
| Cloud Computing, Data owner, Query Processing. |
INTRODUCTION |
| Hosting data-intensive query services in the cloud is increasingly popular because of the unique advantages in scalability, cost-saving andpay for the hours of using the servers. This is an attractive feature because the workloads of query services are highly dynamic, and it will be expensive and inefficient to serve such dynamic workloads with in-house infrastructures [4]. However, because the service providers lose the control over the data in the cloud, data confidentiality and query privacy have become the major concerns. Adversaries, such as curious service providers, can possibly make a copy of the database or eavesdrop users’ queries, which will be difficult to detect and prevent in the cloud infrastructures. |
| While new approaches are needed to preserve data confidentiality and query privacy, the efficiency of query services and the benefits of using the clouds should also be preserved. It will not be meaningful to provide slow query services as a result of security and privacy assurance. Therefore, there is an intricate relationship among the data confidentiality, query privacy, the quality of service, and the economics of using the cloud. We summarize these requirements for constructing a practical query service in the cloud as the CPEL criteria: data Confidentiality, query Privacy, Efficient query processing, and Low in-house processing cost. Satisfying these requirements will dramatically increase the complexity of constructing query services in the cloud. Some related approaches have been developed to address some aspects of the problem. |
| The base paper has proposedRandomSpace Perturbation (RASP) approach toconstructing practical range query and knearest- neighbour (kNN) query services in the cloud. This approach will address all the four aspects of the CPEL criteria and aim to achieve a good balance on them. The basic idea is to randomly transform the multidimensional datasets with a combination of order preserving encryption, dimensionality expansion, random noise injection, and random project, so that the utility for processing range queries is preserved. The RASP perturbation is designed in such a way that the queried ranges are securely transformed into polyhedrain the RASP-perturbed data space, which can be efficiently processed with the support of indexing structures in the perturbed space. The RASP kNN query service (kNN-R) uses the RASP range query service to process kNN queries. The key components in the RASP framework include (1) the definition and properties of RASP perturbation; (2) the construction of the privacy-preserving range query services; (3) the construction of privacy-preserving kNN query services. |
| In summary, the proposed approach has a number of unique contributions. |
| 1. The RASP perturbation is a unique combination of Order Preserving Encryption [3], dimensionality expansion, random noise injection, and random projection, which provides strong confidentiality guarantee. |
| 2. The RASP approach preserves the topology of multidimensional range in secure transformation, which allows indexing and efficiently query pro-cessing. |
| 3. The proposed service constructions are able to minimize the in-house processing workload because of the low perturbation cost and high precision query results. This is an important feature enabling practical cloud-based solutions. |
| For high dimensional data this kNN-R will not work efficiently as it invoke a large number of distance computations and, thus, do neither account for the increasing complexity of the database objects nor for the costly distance functions used for measuring the similarity. Hence we add multi-step query processing algorithm for kNN search using both a lower and an upper bound in the filter step with the above algorithm. We generalize the notion of R-optimality taking the distance estimations available in the filter step into account. Which produces a minimum number of candidates which need to be refined. This multi-step RI kNN-R algorithm is optimal [2]. |
RELATED WORK |
| This section presents the notations, the system architecture, and the threat model for the RASP approach, and prepares for the security analysis [3] in later sections. The design of the system architecture keeps the cloud economics in mind so that most data storage and computing tasks will be done in the cloud. The threat model makes realistic security assumptions and clearly defines the practical threats that the RASP approach will address. |
| Definitions and Notations |
| First, we establish the notations. For simplicity, we consider only single database tables, which can be the result of denormalization from multiple relations. A database table consists of n records and d searchable attributes. We also frequently refer to an attribute as a dimension or a column, which are exchangeable in the paper. Each record can be represented as a vector in the multidimensional space, denoted by low case letters. If a record x is d-dimensional, we say x ∈Rd , where Rd means the d-dimensional vector space. A table is also treated as a d × n matrix, with records represented as column vectors. We use capital letters to represent a table, and indexed capital letters, e.g., Xi, to represent columns. Each column is definedon a numerical domain. Categorical data columns are allows in range query, which are converted to numerical domains as we will describe in Section 3. Range query is an important type of query for many data analytic tasks from simple aggregation to more sophisticated machine learning tasks. Let T be a table and Xi,Xj, and Xk be the real valued attributes in T, and a and b be some constants. Take the counting query for example. A typical range query looks like |
| Selectcount (*) from T where Xi ∈ [ai, bi] and Xj ∈ (aj , bj ) and Xk =ak , |
| which calculates the number of records in the range defined by conditions on Xi, Xj , and Xk . Range queries may be applied to arbitrary number of at- tributes and conditions on these attributes combined with conditional operators “and”/“or”. We call each part of the query condition thatinvolves only one attribute as a simple condition. A simple condition like Xi ∈ [ai, bi] can be described with two half space conditions Xi ≤ bi and −Xi ≤ −ai. Without loss of generality, we will discuss how to process half space conditions like Xi ≤ bi in this paper. A slight modification will extend the discussed algorithms to handle other conditions like Xi <bi and Xi = bi. kNN query is to find the closest k records to the query point, wherethe Euclidean distance is often used to measure the proximity. |
| It is frequently used in location-based services for searchingthe objects close to a query point, and also in machine learning algorithms such as hierarchical clustering and kNN classifier. A kNN query consists of the query point and the number of nearest neighbours, k. |
| System Architecture |
| We assume the cloud computing infrastructure, such as Amazon EC2, is used to host the query services and large datasets. Each record x in the outsourced database contains two parts: the RASP-processed attributes D′ = F (D, K ) and the encrypted original records, Z = E(D, K ′ ), where K and K ′ are keys for perturbation and encryption, respectively. The RASP-perturbed data D′ are for indexing and query processing. Figure1 shows the system architecture for both RASP-based range query service and kNN service. |
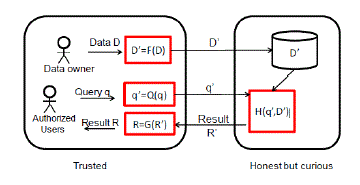 |
| Fig.1.ThesystemarchitectureforRASP-basedquery services. |
| There are two clearly separated groups: the trustedparties and the untrusted parties. The trusted partiesinclude the data/service owner, the in-house proxyserver, and the authorized users who can only submitqueries. The data owner exports the perturbed data tothe cloud. Meanwhile, the authorized users can submit range queries or kNN queries to learn statistics orfind some records. The untrusted parties include thecurious cloud provider who hosts the query servicesand the protected database. The RASP-perturbed datawill be used to build indices to support query processing. |
| There are a number of basic procedures in this framework: (1) F (D) is the RASP perturbation that transforms the original data D to the perturbed data D′ ; (2) Q(q) transforms the original query q to the protected form q′ that can be processed on the perturbed data; (3) H (q′ , D′ ) is the query processing algorithm that returns the result R′ . When the statistics such as SUM or AVG of a specific dimension are needed, RASP can work with partial homomorphic encryption such as Paillier encryption [25] to compute these statistics on the encrypted data, which are then recovered with the procedure G (R′). |
| Threat Model |
| Assumptions.Our security analysis is built on the important features of the architecture. Under this setting, we believe the following assumptions are appropriate. |
| 1. Only the authorized users can query the proprietary database. Authorized users are not malicious and will not intentionally breach the confidentiality. |
| 2. The client-side system and the communication channels are properly secured and no protected data records and queries can be leaked. |
| 3. Adversaries can see the perturbed database, the transformed queries, the whole query processing procedure, the access patterns, and understand the same query returns the same set of results, but nothing else. |
| 4. Adversaries can possibly have the global information of the database, such as the applications of the database, the attribute domains, and possibly the attribute distributions, via other published sources (e.g., the distribution of sales, or patient diseases, in public reports). |
| Attacker Modelling. The goal of attack is to recover (or estimate) the original data from the perturbed data, or identify the exact queries (i.e., location queries) to breach users’ privacy. According to the level of prior knowledge the attacker may have, we categorize the attacks into two categories. |
| Level 1: The attacker knows only the perturbed data and transformed queries, without any other prior knowledge. This corresponds to the cipertext-only attack in the cryptographic set- ting. |
| Level 2: The attacker also knows the original data distributions, including individual attribute distributions and the joint distribution (e.g., the covariance matrix) between attributes. In practice, for some applications, whose statistics are interesting to the public domain, the dimensional distributions might have been published via other sources. |
| These levels of knowledge are appropriate according to the assumptions we hold. |
| Security Definition. Different from the traditional encryption schemes, attackers can also be satisfied with good estimation. Therefore, we will investigate two levels of security definitions: (1) it is computationally intractable for the attacker to recover the exact original data based on the perturbed data; (2) the at- tacker cannot effectively estimate the original data. |
| 2. RASP: RANDOM SPACE PERTURBATION |
| In this section, we present the basic definition of RAndom Space Perturbation (RASP) method and its properties. We will also discuss the attacks on RASP perturbed data, based on the threat model given in Section 2. |
| Definition of RASP |
| RASP is one type of multiplicative perturbation, with a novel combination of OPE, dimension expansion, random noise injection, and random projection. Let’s consider the multidimensional data are numeric and in multidimensional vector space1. The database has k searchable dimensions and n records, which makes a d × n matrixX. The searchable dimensions can be used in queries and thus should be indexed. Let x represent a d-dimensional record, x ∈ Rd. Note that in the d-dimensional vector space Rd, the range query conditions are represented as half-space functions and a range query is translated to finding the point set in corresponding polyhedron area described by the half spaces [10]. |
| The RASP perturbation involves three steps. Its security is based on the existence of random invertible real-value matrix generator and random real value generator. For each k-dimensional input vector x, |
| 1. An order preserving encryption (OPE) scheme [3], Eope with keys Kope, is applied to each dimension of x: Eope(x, Kope) ∈ Rd to change the dimensional distributions to normal distributions with each dimension’s value order still preserved. |
| 2. The vector is then extended to d + 2 dimensions as G(x) = ((Eope(x))T , 1, v)T , where the (d + 1)th dimension is always a 1 and the (d + 2)th dimension, v, is drawn from a random real number generator RN G that generates random values from a tailored normal distributions. We will discuss the design of RNG and OPE later. |
| 3. The (d + 2)-dimensional vector is finally transformed to |
| F (x, K = {A, Kope, RG}) = A((Eope(x))T , 1, v)T (1) |
| Where A is a (d + 2) × (d + 2) randomly generated invertible matrix with aij∈R such that there are at least two non-zero values in each row of A and the last column of A is also non-zero2. |
| Kope and A are shared by all vectors in the database, but v is randomly generated for each individual vector. Since the RASP-perturbed data records are only used for indexing and helping query processing, there is no need to recover the perturbed data. As we mentioned, in the case that original records are needed, the encrypted records associated with the RASP-perturbed records will be returned. We give the detailed algorithm in Appendix. |
| Design of OPE and RNG. We use the OPE scheme to convert all dimensions of the original data to the standard normaldistribution N (0, 1) in the limited domain [−β, β]. β can be selected as a value >= 4, as the range [−4, 4] covers more than 99% of the population. This can be done with an algorithm such as the one described in [1]. The use of OPE allows queries to be correctly transformed and processed. Similarly, we draw random noises v from N (0, 1) in the limited domain [−β, β]. Such a design makes the extended noise dimension indifferent from the data dimensions in terms of the distributions. |
| The design of such an extended data vector (Eope(x) T, 1, v) Tis to enhance the data and query confidentiality. The use of OPE is to transform large-scale or infinite domains to normal distributions, which address the distributional attack. The (d + 1) th homogeneous dimension is for hiding the query content. The (d + 2)th dimension injects random noise in the perturbed data and also protects the transformed queries from attacks. The rationale behind different aspects will be discussed clearly in later sections. |
| Properties of RASP |
| RASP has several important features. First, RASP does not preserve the order of dimensional values be- cause of the matrix multiplication component, which distinguishes itself from order preserving encryption (OPE) schemes, and thus does not suffer from the distribution-based attack[1]. An OPE scheme maps a set of single-dimensional values to another, while keeping the value order unchanged. Since the RASP perturbation can be treated as a combined transformation F (G(Eope (x))), it is sufficient to show that F (y) = Ay does not preserve the order of dimensional values, where y ∈ Rd+2 andA ∈ R(d+2)×(d+2) [1]. Second, RASP does not preserve the distances between records, which prevents the perturbed data from distance-based attacks [6]. Because none of the transformations in the RASP: Eope, G, and F preserves distances, apparently the RASP perturbation will not preserve distances. Similarly, RASP does not preserve other more sophisticated structures such as covariance matrix and principal components [7]. Therefore, the PCA-based attacks such as [8], [9] do not work as well. Third, the original range queries can be transformed to the RASP perturbed data space, which is the basis of our query processing strategy. A range query describes a hyper-cubic area (with possibly open bounds) in the multidimensional space. In Section 5, we will show that a hyper-cubic area in the original space is transformed to a polyhedron with the RASP perturbation. Thus, we can search the points in the polyhedron to get the query results. |
| Multi-step kNN Query Processing |
| Let D be a database of objects and dist be a distance function on these objects.For a given query object q and a given positive integer k ∈N+, a k-nearest neighbour (kNN) query on a database D retrieves the objects in D that have the k smallest distances to q, formally |
| Definition 1: (kNN query, kNN-distance). For a query object q and a query parameter k ∈N, a kNN query in D returns the smallest set NND(q, k)⊆ Dthat contains (at least) k objects from D, for which the following condition holds: ∀o ∈NN D (q, k), ∀o’ ∈ D−NND(q, k):dist(q, o) <dist(o’, q) |
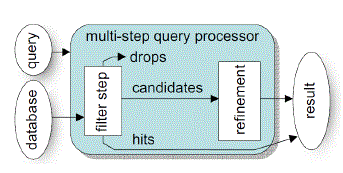 |
| Fig. 2. Multi step query processor. |
| The multi-step kNN search method is the algorithm proposed in [11]. It uses a lower-bounding distance estimation LB in the filter step which is always lower or equal to the exact distance, i.e. for any query object q the lower bounding property holds. |
| ∀o ∈D:LB(q, o) ≤ dist(q, o) |
| Generalizing the Definition of Optimality: |
| As indicated above, the algorithm presented in [11] uses only a lower bounding distance estimation in the filter step. However, it is in general sensible to use additional information, in particular an upper bounding filter distance. An upper bounding filter distance estimation UB is always greater or equal to the exact distance, i.e. for any query object q the following upper bounding property holds: |
| ∀o ∈D : UB(q, o) ≥ dist(q, o). |
| Using also an upper bounding filter distance yields several important advantages: First, besides pruning true drops with the lower bound we can additionally identify true hits using the upper bounding filter distance. Second, the storage requirements of the kNN algorithm can be significantly reduced. Third, the filter step is the fact that those true hits, identified already in the filter step, can be immediately reported to the user. |
RASP RANGE-QUERY PROCESSING |
| Based on the RASP perturbation method, we design the services for two types of queries: range query and kNN query. This section will dedicate to range query processing. We will first show that a range query in the original space can be transformed to a polyhedron query in the perturbed space, and then we develop a secure way to do the query transformation. Then, we will develop a two-stage query processing strategy for efficient range query processing. |
| Transforming Range Queries |
| Let’s look at the general form of a range query condition. Let Xi be an attribute in the database. A simple condition in a range query involves only one attribute and is of the form “Xi <op>ai”, whereaiis a constant in the normalized domain of Xi andop ∈ {<, >, =, ≤, ≥, =} is a comparison operator. Forconvenience we will only discuss how to processXi <ai, while the proposed method can be slightlychanged for other conditions. Any complicated rangequery can be transformed into the disjunction of a set of conjunctions. Again, to simplify the presentation we restrict our discussion to a single conjunction condition ∩i=1 Ci , where Ci is in form of bi ≤ Xi ≤ ai. Such a conjunction condition describes a hyper-cubic area in multidimensional space. |
| According to three nested transformation in RASP F (G (Eope(x))), we will transform the original hyper-cubic area to another hyper-cubic area in the OPE space. |
| Let y= Eope (x) and ci= Eope (ai). A simplecondition Yi≤ cidefines a half-space. With theextended dimensions zT = (yT , 1, v), the half-space can be represented as wT z ≤ 0, where w is a d + 2 dimensional vector with wi = 1, wd+1 = −ci, andwj = 0 for j = i, d + 1. |
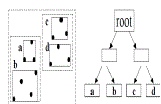 |
| Fig. 3.R-tree index. |
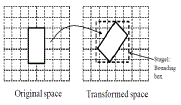 |
| Fig. 4.Illustration of the two-stage processing algorithm. |
| Finally, let u = Az, according to the RASP transformation. With this representation, the original condition is equivalent to |
| wTA−1u≤0 (3) |
| In the RASP-perturbed space, which is still a half- space condition. However, this half-space condition will not be parallel to the coordinate - these trans- formed conditions together form a polyhedron (as illustrated in Figure 4. The query service will need to find the records in the polyhedron area, which is supported by the two-stage processing algorithm. |
| b. A Two-Stage Query Processing Strategy with Multidimensional Index Tree |
| With the transformed queries, the next important task is to process queries efficientlyand return precise results to minimize the client-side post-processing effects. A commonly used method is to use multi- dimensional tree indices to improve the search performance. However, multidimensional tree indices are normally used to process axis-aligned “bounding boxes”; whereas, the transformed queries are in arbitrary polyhedra, not necessarily aligned to axes. In this |
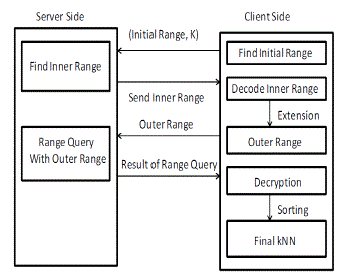 |
| Fig. 5. Procedure of KNN-R algorithm |
| section, we propose a two-stage query processing strategy to handle such irregular-shape queries in the perturbed space. |
| MultidimensionalIndex Tree.Most multidimensional indexing algorithms are derived from R-tree like algorithms 2], where the axis-aligned minimum bounding region (MBR) is the construction block for indexing the multidimensional data. For 2D data, an MBR is a rectangle. For higher dimensions, the shape of MBR is extended to hyper-cube. Figure 3 shows the MBRs in the R-tree for a 2D dataset, where each node is bounded by a node MBR. The R-tree range query algorithm compares the MBR and the queried range to find the answers. |
| The Two-StageProcessing Algorithm.The transformed query describes a polyhedron in the perturbed space that cannot be directly processed by multi-dimensional tree algorithms. New tree search algorithms could be designed to use arbitrary polyhedron conditions directly for search. However, we use a simpler two-stage solution that keeps the existing tree search algorithms unchanged. At the first stage, the proxy in the client side finds the MBR of the polyhedron (as a part of the submitted transformed query) and submit the MBR and a set of secured query conditions {Θ1 , . . . , Θm } to the server. The server then uses the tree index to find the set of records enclosed by the MBR. The MBR of the polyhedron can be efficiently founded based on the original range. The original query condition constructs a hyper-cube shape. With the described query transformation, the vertices of the hyper cube are also transformedto verticesof the polyhedron. Therefore, the MBR of the vertices is also the MBR of the polyhedron [13]. Figure 4 illustrates the relationship between the vertices and the MBR and the two-stage processing strategy. |
| At the second stage, the server uses the transformed halfspace conditions to filter the initial result. In most cases of tight ranges, the initial result set will be reasonably small so that it can be filtered in memory by simply checking the transformed half-space conditions. However, in the worst case, the MBR of the polyhedron will possibly enclose the entire dataset and the second stage is reduced to a linear scan of the entire dataset. The result of second stage will return the exact range query result to the proxy server, which significantly reduces the post-processing cost that the proxy server needs to take. It is very important to the cloud-based service, because low post-processing cos requires low inhouse investment. |
KNN QUERY PROCESSING WITH RASP |
| Because the RASP perturbation does not preserve distances (and distance orders), kNN query cannot be directly processed with the RASP perturbed data. In this section, we design a kNN query processing algorithm based on range queries (the kNN-R algorithm). As a result, the use of index in range query processing also enables fast processing of kNN queries |
| Overview of the kNN-R Algorithm |
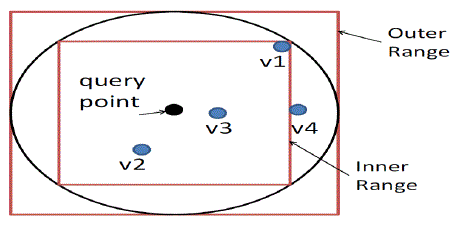 |
| Fig. 6. Illustration of kNN Algorithm when k=3 |
| The original distance-based kNN query processing finds the nearest k points in the spherical range that is centered at the query point. The basic idea of our algorithm is to use square ranges, instead of spherical ranges, to find the approximate kNN results, so that the RASP range query service can be used. There are a number of key problemsto make this work securely and efficiently. (1) How to efficiently find the minimum square range that surely contains the k results, without many interactions between the cloud and the client? (2) Will this solution preserve data confidentiality and query privacy? (3) Will the proxy server’s workload increase? To what extent? |
| The algorithm is based on square ranges to approximately find the kNN candidates for a query point. Figure 6 illustrates the range-query-based kNN processing with two-dimensional data. The Inner Range is the square range that contains at least k points, and the Outer Range encloses the spherical range that encloses the inner range. The outer range surely contains the kNN results (Proposition 2) [1] but it may also contain irrelevant points that need to be filtered out. |
| The kNN-R algorithm consists of two rounds of interactions between the client and the server. Figure 5 demonstrates the procedure. (1) The client will send the initial upper-bound range, which contains more than k points, and the initial lower-bound range, which contains less than k points, to the server. The server finds the inner range and returns to the client. (2) The client calculates the outer range based on the inner range and sends it back to the server. The server finds the records in the outer range and sends them to the client. (3) The client decrypts the records and find the top k candidates as the final result. |
| a. FindingInner Rangewith RASP Perturbed Data |
| Algorithm 4 gives the basic ideas of finding the compact inner range in iterations. There are two critical operations in this algorithm: (1) finding the number of points in a square range and (2) updating the higher and lower bounds. Because range queries are secured in the RASP framework, the key is to update the bounds with the secured range queries, without the help of the client-side proxy server. As discussed in the RASP query processing, a range query such as S(L) is encoded as the MBR(L) of its polyhedron range in the perturbed space and the 2(d+2)dimensional conditions. yT Θ(L) y ≤ 0 determining the sides of the polyhedron, and each of the d + 2 extended dimensions gets a pair of conditions for the upper and lower bounds, respectively. |
| The problem of binary range search is to use the higher bound range S(high) and lower bound range S(low) to derive S(mid). When all of these ranges are secured, the problem is transformed to (1) deriving Θi fromΘi and Θi; and (2) derivingMBR (mid) fromMBR (high) andMBR (low). The following discussion will be focused on the simplified RASP version without the OPE component, which will be extended with the OPE component (Proposition 3) [1]. |
| As we have mentioned, the MBR of an arbitrary polyhedron can be derived based on the vertices of the polyhedron. A polyhedron is mapped to another polyhedron after the RASP perturbation. Concretely, let a polyhedron P has m vertices {x1, . . . ,xm}, which are mapped to the vertices in the perturbed space: {y1, . . . , ym}. Then, the upper bound and lower bound of dimension j of the MBR of the polyhedron in the perturbed space are determined by max{yij , i =1 . . . m} and min{yij , i = 1 . . . m}, respectively. |
| Let the j-th dimension of M BR(L) represented as [s(L) j,min , S(L) j,max], where s(L) j,min = min{yij , i = 1 . . . m}, S(L) j,max = max{yij (high) , i = 1 . . . m}. Now we choose the MBR(M I D) as follows: for j-th dimension we use [(s(L) j,min + s(H) j,min) /2, (S(L) j,max + S(H) j,max)/2] (Proposition 4)[1]. |
| Including the OPE component.The results onΘ (mid) and MBR(M I D) can be extended to the RASP scheme with the OPE component. However, due to the introduction of the order preserving function fi (), the middle point may not be strictly the middle point, but somewhere between the higher bound and lower bound. We use “between” (btw) to denote it. Specifically, if Xi < h and Xi < l are the corresponding conditions for the higher and lower bounds. Let the condition for the “between” bound be Xi < b that satisfies fi (b) = (fi (h) + fi (l))/2. According to the OPE property, we have l < b < h, i.e., the corresponding range is still between the lower range and higher range. Therefore, the same binary search algorithm can still be applied. |
| b. RIlu-optimal Multi-step kNN-R Search |
| The state-of-the-artmulti-step k-nearest neighbour (kNN) search algorithms are designed touse only a lower bounding distance estimation for candidate pruning. The generalized the traditional concept of R-optimality and introduce the notion of RI-optimality depending on the distance information I available in the filter step is described in [2]. It describes multi-step kNN search algorithm that utilizes lower- and upper bounding distance information (Ilu) in the filter step. Furthermore, it show that, in contrast to existing approaches, proposed solution is RIlu - optimal. The Algorithm in [2] shows the pseudo-code of this method.The algorithmiteratively reduces the candidate set, where in each iteration it identifies truedrops, true hits and/or refines a candidate for which the query predicate cannotbe determined without the refinement.This method uses the lower bound and upper bound sent by the client (RI-Optimal k-NN Algorithm). |
| Now we propose an algorithm which uses the inner bound obtained from the kNN-R algorithm. The inner bound which is also called as lower bound is calculated in section 6. Algorithm 1 will return the S (mid)value which will be used in the proposed algorithm as lower bound dmin |
| TheRIlu-optimal Multi-step kNN-R algorithm starts with the initialization of the incremental ranking on theused index according to the lower-bounding distances of all objects. Then, the first k candidates are fetched from the ranking sequence into the candidate list (Step 1). In order to detect which candidate must be refined, we use two variablesdmin and dmax generating a S(mid) and an upper-bounding distance estimation of the exact k-NN distance, i.e. dmin ≤ nnk−dist(q,D) ≤ dmax. The basic idea of our algorithm is that we can use this restriction of the exact k-NN distance in order to identify those candidates c with LB (q, c) ≤ nnk−dist (q, D) ≤UB (q, c) which must be refined due to Lemma 1[2]. Furthermore, as the stop criterion of the main loop, we initialize the variable dfnextreflecting the lowerbounding distance of the top element of the ranking sequence to q. |
| In the main loop, we first update the variables dmin, dmax and dfnext as depicted. Then, we fetch the next candidate o from the ranking sequence into the candidate set candidates, if dmin ≥ df next holds (Step 2). This condition guarantees that we fetch only the next candidate from the ranking query if the variable dmin does not guarantee the conservative estimation of the exact k-NN distance any more. This ensures the RIlu-optimality of the algorithm and guarantees that our algorithm does not produce unnecessary candidates. Then, the lower-bounding distance estimation of the newly fetched candidate must lie on the new dmin value after the update of the dminvariable. Hence, the fetch candidate either is a true hit or covers the exact kNN-distance, and thus, must be refined. This guarantees, that our algorithm is optimal w.r.t. the number of fetches from the ranking sequence which in turn is responsible for the optimality according to the number of index accesses. Let us note, that our fetch routine additionally hands over the actual dmax value to the ranking query method. This allows us to proceed the exploration of the index only when necessary and to cut the priority queue according to dmax in order to decrease the size of the queue. After fetching a new candidate, we have to update the variables dmin, dmaxand dfnext in order to keep the consistency of the used distance estimation variables.Step 3 of the algorithm identifies the hits and drops according to the dminand dmax values. Obviously, all candidates c with UB (q, c) <dmincan be returned immediately as hits and all candidates c’\ with LB (q, c_) >dmaxcan be pruned. Next, if the number of received results plus the remaining number of candidates are greater than k and if the condition df next ≤ dmaxholds, then we refine the next candidate (Step 4). The first condition indicates whether it is still necessary to refine a candidate. The reason for this condition is, that, if the remaining candidates definitely must belong to the query result because there are no concurrent candidates available any more, we can stop the refinement and immediately report the remaining candidates as hits. If both conditions hold, the algorithm refines a candidate c with LB (q, c) ≤dmin and dmax ≤ UB (q, c). |
| As mentioned above, this procedure guarantees the RIlu-kNN-R optimality of this algorithm. If dfnext> dmax, i.e. the top element of the ranking sequence can be pruned as true drop or if there are no more candidates left, the main loop stops. In the following, we show that our algorithm RI kNN-ROptimal is (1) fetch optimal in the number of fetches from the ranking sequence, (2) correct, and (3) RIlu-optimal. Let us note, that fetch optimal corresponds to a minimal number of disk accesses of the underlying index on which the ranking sequence is computed when using access optimal ranking query algorithms. |
| In summary, assuming that a lower- and upper-bounding filter distance is available for each processed object, our novel multi-step kNN-R algorithm is correct, requires the minimal number of index page accesses, optimal w.r.t. the number of refinements required to answer the query and protected. |
CONCLUSION |
| We propose the RASP perturbation approach to hosting query services in the cloud, which satisfies the CPEL criteria: data Confidentiality, query Privacy, Efficient query processing, and Low in-house work- load. The requirement on low in-house workload is a critical feature to fully realize the benefits of cloud computing, and efficient query processing is a key measure of the quality of query services. |
| RASP perturbation is a unique composition of OPE, dimensionality expansion, random noise injection, and random projection, which provides unique security features. It aims to preserve the topology of the queried range in the perturbed space, and allows to use indices for efficient range query processing. With the topology-preserving features, we are able to develop efficient range query services to achieve sub- linear time complexity of processing queries. We then develop the kNN query service based on the range query service. As it was practically proved that kNN-R will not work efficiently for high dimensional data as it requires require a lot of distance computations. So, we used the inner bound obtained in kNN-R algorithm as the lower bound in RI kNN-R Optimal Algorithm and proposed a new algorithm called RI kNN-R Optimal. As this algorithm uses both lower and upper bound it does not produce unnecessary candidates and will be more effective on high dimensional data. |
 |
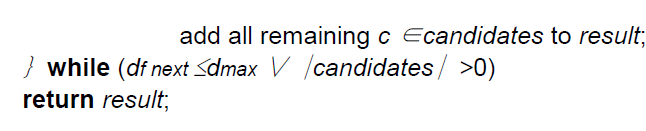 |
References |
|