ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Mansoor Farooq PhD Scholar, Department of Computer Science, Shri Venkatashwara University, U.P. India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this research paper we use combination of stochastic algorithms and hybrid intelligent systems for pattern recognition or classification. Stochastic algorithm has been used for model selection of components or classification, especially when the dimension of the patterns is high. Genetic algorithms are one of the commonly used techniques for stochastic classifiers. Hybrid Intelligent Systems (HIS) combine intelligent techniques in synergistic architectures in order to provide solutions for complex problems. These systems utilize at least two of the three techniques: fuzzy logic, genetic algorithms and neural networks. The aim of their combination is to amplify their strengths and complement their weaknesses. A good architecture for a hybrid system should match each of its tasks to the appropriate intelligent technique and provide an efficient means for their integration. However, it is not always obvious or easy to build HIS architectures that achieve the higher intelligence goal. A good architecture for a hybrid system should match each of its tasks to the appropriate intelligent technique and provide an efficient means for their integration.
Keywords |
| Genetic Algorithm, Hybrid Intelligent Systems and Pattern Recognition |
INTRODUCTION |
| Pattern recognition is an established field of research with a wide variety of applications in fields such as speech recognition, image processing, and signal analysis. Many of the developed techniques of pattern recognition [2] have been applied successfully to a variety of real problems. However, there are always new applications that have different types of patterns that render the existing algorithms unable to handle them. The primary goal of pattern recognition is pattern classification [2]. In general, pattern classification techniques can be divided into two main categories [2]: supervised and unsupervised techniques. In supervised classification the classes and their boundaries are determined or at least defined by the designer of the classification system before training the classifier. On the other hand, in unsupervised learning the system learns the boundaries of the classes based on the similarity between groups of patterns. |
| Pattern classification techniques can also be categorized based on the type of algorithm used. An important group of techniques is statistical pattern classification. In these techniques a given pattern is assigned to a certain category based on a vector of features. Each class is assumed to define a probability density function for these features. The conditional probability of a pattern belonging to a certain class is computed and decision rules like Bayesian decision rule or maximum likelihood are applied [2] to determine the class of a given pattern. More recently, neural network techniques and methods imported from statistical learning theory have been receiving increasing attention. Stochastic methods and unsupervised learning techniques are also among the actively studied techniques. |
| Despite the number of different classification techniques, there are many applications that still require more powerful classification systems. A promising way for developing these systems is to combine more than one technique in unified classifier architectures. This type of combination is also called hybridization. The field of hybrid systems is still a new field of research and there is a lot to be accomplished in it. The design of a recognition system for a specific application requires careful attention to the following issues: definition of pattern classes, sensing environment, pattern representation, feature extraction and selection, cluster analysis, classifier design and learning procedure [2]. In this paper, we will focus on hybrid intelligent systems for pattern recognition. |
RELATED WORK |
| Most reported systems in the literature deal with the voluminous data collection using some feature extraction method. Note that the original pattern is basically a 2-D function that relates time to the measured attribute reading. Each reading point is considered to be a feature. The main two techniques used for feature extraction select 60 or 72 points per 480. After that, only six of the extracted features are put together to form a vector that represents the pattern to the classifier. The main concept is to reduce the 2-D large sequence of points describing the pattern to a 1-D vector representation with a minimal number of elements that enable reasonable classification performance. Thus each pattern is converted to a point in a higher dimensional space, e.g. 6 instead of being described by a large sequence of points in 2-D space. Obviously, this method involves loss of information since the location in the time domain where the original important feature happened is lost. The main driver for this approach might be the dependence classification techniques like Principal Component Analysis and Linear Discriminant Analysis that can handle vectors with limited numbers of elements (dimensions). |
| In the real domain the number of values representing a pattern in is huge. For Example 1024 values to represent each pattern. This large number of values is not suitable for commonly used pattern classification algorithms such as clustering and neural network techniques. This problem is usually called the problem of high dimensionality [11]. A commonly used technique for overcoming this problem is feature extraction. The basic idea is to extract the important features of the pattern and use these in the pattern classification instead of the full pattern description in the real domain. Therefore to achieve our goal of being able to handle large numbers of classes we developed the concept of the abstract domain. In this domain the pattern is described by a set of features made out of simple shapes rather than a selected vector. Simple shapes can be triangles, rectangles, or any other polygonal shape. The idea here is take a sequence of values from the large data vector and represent them with the shape. Note that we also keep the location of the shape. |
| As we have chosen a binary decision tree as the overall architecture for decision tree classifiers, the tree building process starts with a training pattern set Strain, then a classification rule is chosen and a node is added to the tree to capture this rule. The training set is subdivided into subsets based on the chosen rule, which will be discussed later. The same process for choosing rules and adding nodes is repeated recursively until the pattern subset contains patterns from one class. At this point a leaf is added to the tree and the class information is attached to it. The classification tree is fully built when all the classes of the training set have been represented by leaves in the tree. The classification rules we use in HIS is expressed as: |
| IF (Sim(x, m) > t ) THEN visit the Pass-Child node ELSE visit Fail-Child node, where Sim(x, m) is a similarity measure between a signal pattern x and a set of important features, called the mask, m and t is a similarity cutoff value [8]. The roles of the three components of the decision tree classification rules. The feature mask component represents a set of reference characteristics that describe clusters of classes while the similarity measure is the comparison tool for comparing patterns in the abstract domain. The rule cutoff value defines class boundaries in the abstract domain. This is different from the basic pattern classification where the boundaries are defined in the input data domain. |
GENETIC ALGORITHM IN HYBRID INTELLIGENT SYSTEM FOR PATTERN RECOGNITION |
| Genetic algorithms are great tool for global search and optimization but their performance is not guaranteed [1]. The goal of HIS is to complement the weaknesses of these techniques and integrate their strengths. IF (Sim(x, m) > t ) THEN visit the Pass-Child node ELSE visit Fail-Child node. The main component of the rule antecedent is computation of the similarity of the pattern x to a set of important features m, called a mask. In general, a feature mask is a set of features that might be composed of a partial pattern, a subset of features from more than one pattern or even a set of features that are not found in any of the training pattern set Strain. Obviously, the problem of selecting high quality feature masks can be formulated as a search problem over the space of all features related to a training set Strain. The goal of the search algorithm is to find the feature masks with the highest ability to discriminate among the members of the training set Strain. It is clear that the search space is infinite since we not only allow feature masks to be composed of any subsets of all features in Strain but also from features that do not exist in Strain. Our HIS implementation uses Matlab [5] due to its flexibility in system modelling and the availability of many toolboxes that implement commonly used algorithms. We used a publicly available Matlab toolbox GAOT [53] due to its capability of handling real number encoding of chromosomes. |
| Finding Pattern Masks Using GA |
| Genetic algorithms are excellent at searching large spaces to find solutions with the highest performance [10]. Their high efficiency is attributed to the way they generate and evaluate many individuals making up a generation. Crossover processes help preserving the best traits through the generations. Mutation introduces a random minor perturbation to the selected individuals to allow exploration of different regions in the search space instead of allowing the search to become trapped near local extreme points. Our goal is to develop a hybrid intelligent classifier that employs the different intelligent techniques to solve pieces of the problem. The first step to apply a genetic algorithm to the problem of feature mask selection is encoding the problem in some chromosome format and defining the fitness function that guides the genetic algorithm. The second step is to determine the genetic operators and then tune them to the best performance. |
| GA Parameters |
| A genetic algorithm [10] is utilized to find the best pattern mask for each node in the classification tree. Each pattern mask is made of n features that can vary among pattern masks. We discuss below the basic constructs used for the genetic algorithm in hybrid intelligent system pattern classifiers. |
| Encoding in hybrid pattern classifier is done by using strings of real-valued numbers. Each feature in the mask is represented by its attributes, i.e., start and end locations, height and area. The mask string is composed of the sequence of its encoded features. |
| Initial population in hybrid pattern classifier is generated by picking m signal patterns from the pattern set associated with the node. For each pattern in m we pick the biggest n features in area and encode them to make an individual mask string. |
| Fitness is very crucial to the performance of hybrid pattern classifier. There are many possibilities to measure the fitness of a pattern mask. One fitness measure based on the infomax concept used in decision trees [6]. The more evenly the rule divides the pattern set, the higher its fitness score. This will lead to a shallower classification tree and lower classification cost. Therefore we devised a fitness measure that takes into account the characteristics of the clusters generated by the pattern mask. |
| Selection methods include roulette wheel selection and ranking selection. Any of these methods is applicable to pattern classifiers. Our current implementation uses roulette wheel selection. |
| Crossover methods that apply to real numbers can be used in pattern classifier since the pattern masks are encoded as real number strings. |
| Mutation in hybrid pattern classifier is done by using non-uniform mutation; however any of the mutation methods applicable to real number strings can be used as well. |
| Termination condition in hybrid pattern classifier can be set to a certain level of mask fitness or a limit on the number of generations. Note that the termination condition can be different for different nodes in the tree. |
| Each component of the algorithm has different parameters that need to be set to optimize hybrid pattern classifier’s performance. Selection of these parameters is based on running many tests, varying one parameter at a time to determine the value that gives the best performance. Our system design evolution process is an iterative process where each iteration includes a tuning step to optimize the added component parameters. Selection of the GA parameters fits in the tuning step. In this first iteration our focus was to utilize and tune the GA to find the best feature masks. However we also needed to define similarity cutoff values and the similarity measure. |
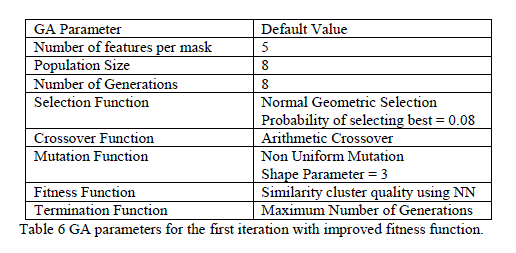
| Cutoff values were encoded at the end of the feature mask chromosomes. The chromosomes’ fitness was computed as the ratio of the smaller subset size, pass or fail subset, to the total pattern set size associated with the node for which the GA is working on finding the feature mask. In each case, the classification tree was built to have leaves each containing one class only. Table 1 shows the task assignment of hybrid pattern classifier while Table 2 shows the parameters of the test. Table 3. shows the default parameters of the GA for testing. |
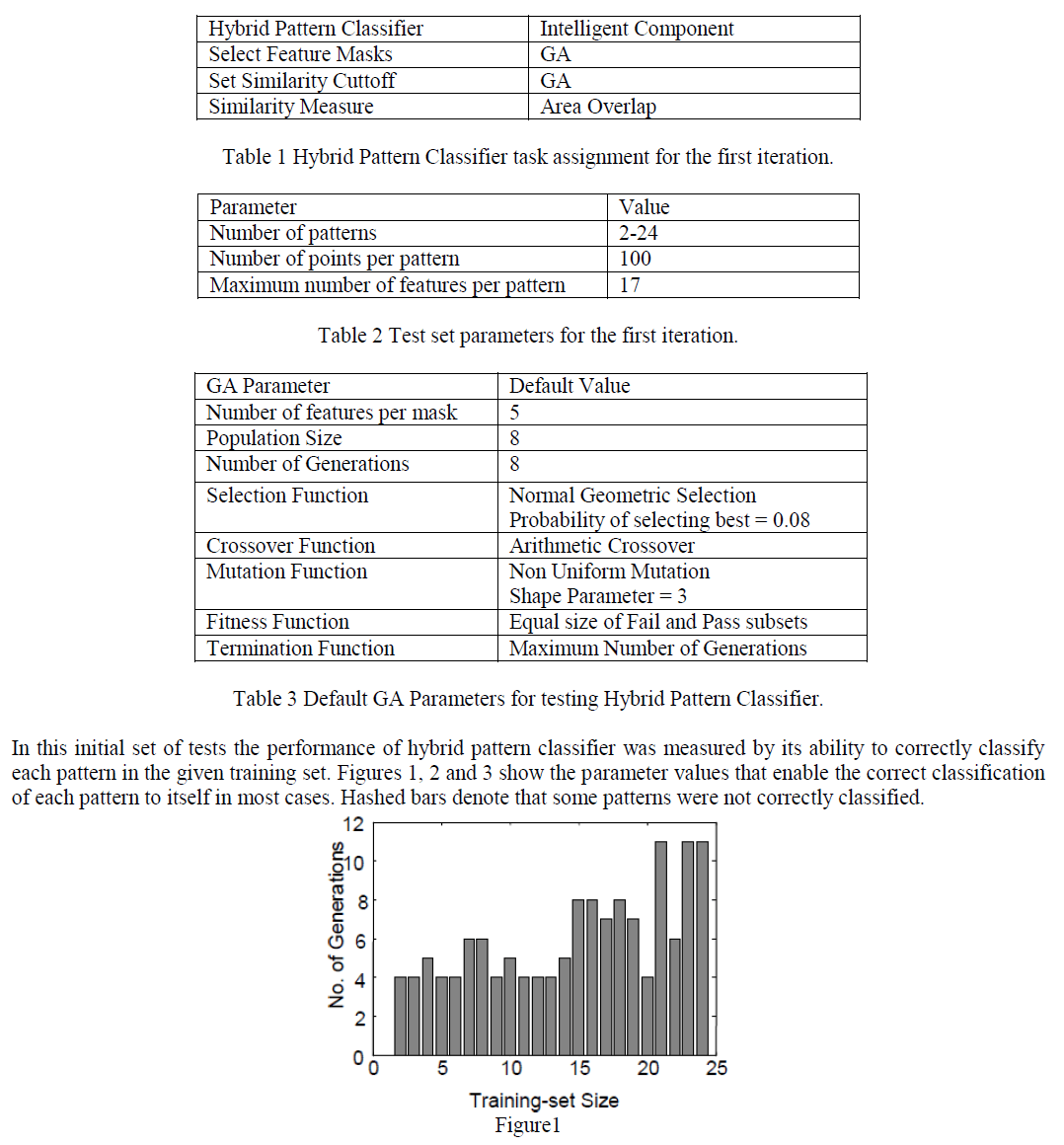 |
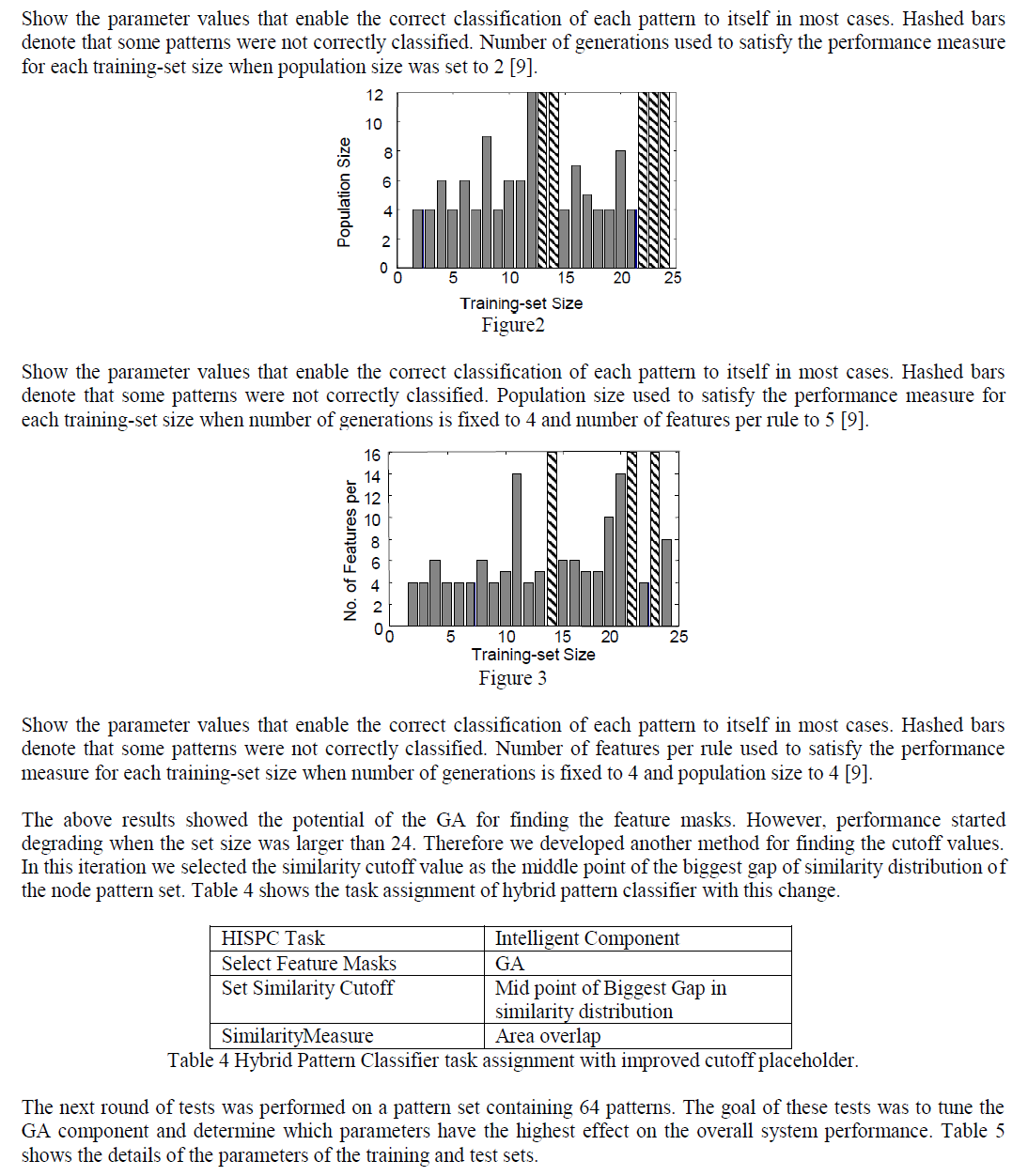 |
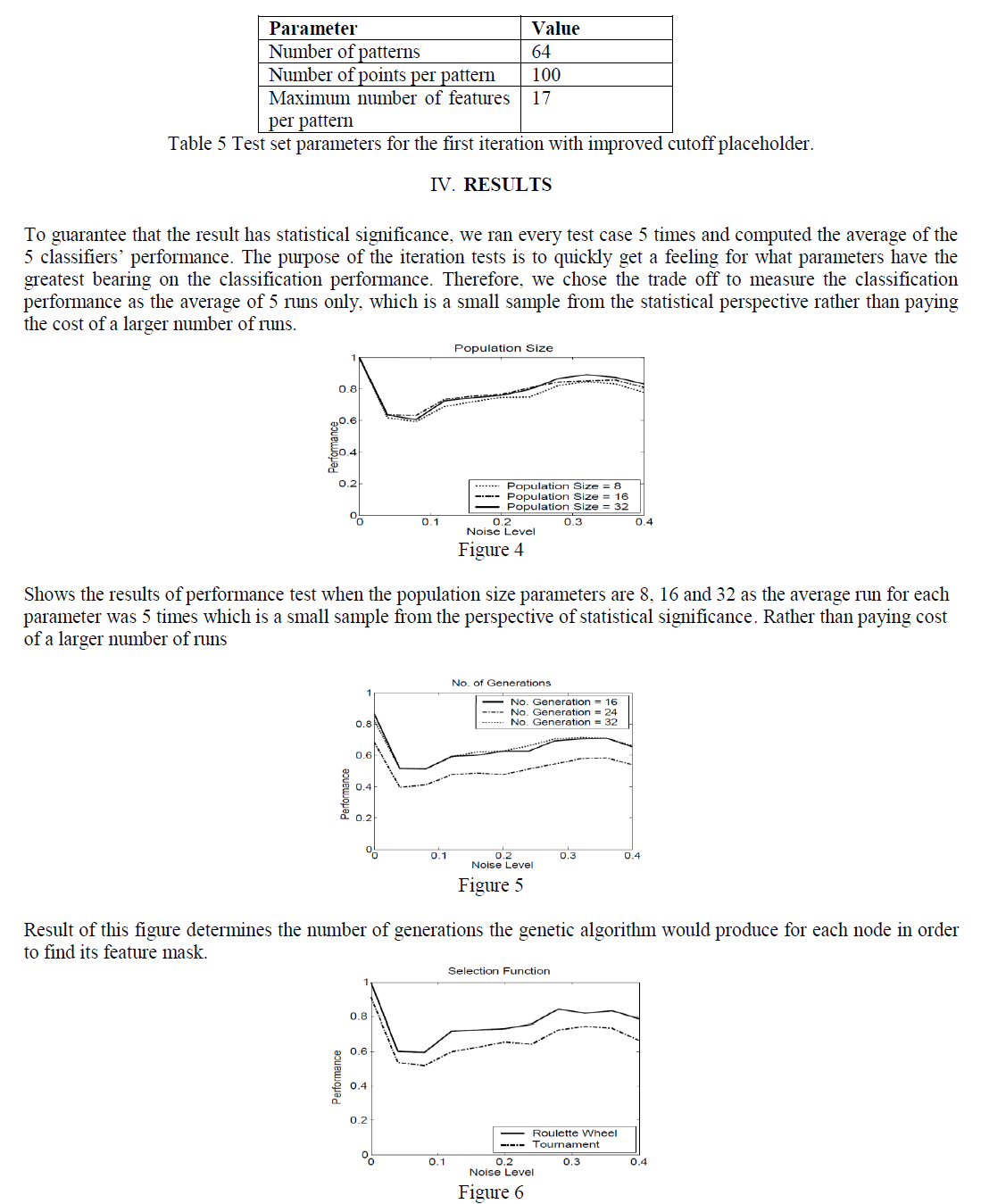 |
 |
 |
CONCLUSION |
| In the course of this paper we have covered many aspects of pattern classification using hybrid intelligent systems. The paper has tried to answer questions in pattern classification, hybrid intelligent systems and genetic algorithm approach in general. The goals set of this paper has been met as shown by the various testing results. The hybrid pattern classification developed through this paper provided an excellent means for studying ways of combining different intelligent techniques. It also enabled investigation of the effects of the various parameters of each technique on the overall performance. We have also introduced the concept of feature masks that allow the classifier to define class boundaries in terms in subsets of features instead of one feature at a time. For example in regular decision trees every node usually has classification rules based on one parameter of the pattern. However, we used a pattern mask that combined a subset of features along with their location to define the class boundaries. Each technique has its effectiveness in solving part of the problem. Genetic algorithms are powerful in searching the large space of similarity rules and are very effective in setting the class boundaries cutoff values and evaluating feature mask fitness. |
References |
|