ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| S.Manoharan, Dr.K.Gnanambal , R .Girija, K.P.Ram Prasath Department of Electrical and Electronics Engineering, K.L.N College of Engineering, Madurai, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Distributed Generation (DG) System is a small scale electric power generation which is based on wind energy, fuel cell, photo voltaic system, hydro etc. Grid Synchronization is one of the most important issues in the control of inverters connected to the grid. The proper operation of grid connected inverter system is determined by grid voltage conditions such as phase, amplitude and frequency. A discrete phase-locked loop (PLL) is used to track the phase angle in order to improve the synchronization systems response in adverse grid conditions. Using the enhanced synchronization structure the fundamental positive-sequence component of grid voltages in asymmetric and distorted three-phase systems is estimated. The α-β stationary frame is used to obtain the pulsation for grid inverter using a space vector pulse width modulation (SVPWM). The performance of the proposed structure is verified through simulations using a grid set of ideal and non-ideal grid conditions (three-phase voltage unbalance, variation in frequency, variation in amplitude and phase shift).The simulation results demonstrates that the proposed method is very effective in digital structure synchronization .
Keywords |
| Distributed Generation (DG), discrete phase-locked loop (PLL), synchronization systems, positive-sequence component, SVPWM, non-ideal grid conditions. |
INTRODUCTION |
| The Distributed Generation (DG) systems are highly sporadic power generation system and their power output depends heavily on the natural conditions. Various grid code requirements must be met to connect the DG systems with the utility grid. To ensure safe and reliable operation of power system based on DG system [1], usually power plant operators should satisfy the grid code requirements such as fault ride through, power quality improvement, grid synchronization, grid stability and power control etc. |
| The grid synchronization techniques can be adversely affected by the application of a disturbing influence (influence quantity) on the electrical input signals. Due to the increase in number of Distributed Generation (DG) Systems has lead to complexity in control while integrating into grid. As a result requirements of grid connected inverters become stricter and stricter to meet very high power quality standards. |
| Grid voltage conditions such as phase, amplitude and frequency determine the proper operation of a grid connected system. In such applications, a fast and accurate detection of the phase angle, frequency and amplitude of the grid voltage is essential. These factors, together with the implementation simplicity and the cost are all important when examining the credibility of a synchronization scheme. Therefore an ideal phase-detection scheme must be used to promptly and smoothly track the grid phase through various short-term disturbances [2] [3] and long term disturbances to set the energy transfer between the grid and the power converter. |
| One of the earliest methods used for tracking the phase angle is Zero Crossing Detector (ZCD) method [4], but the performance of ZCD is badly affected by power quality phenomena [5]. The Linear PLL is mainly used to detect phase for single phase supply. Use of voltage controlled oscillators (VCOs) resulted in more rigid controllers such as the Phase Locked Oscillator systems and the Charge-Pump PLLs. However with the development of discrete devices such as microcontrollers, various high performance synchronization methods have been introduced. |
| The most recently proposed technique that can be used for grid synchronization is the phase-locked loop (PLL); it is a control system that generates an output signal whose phase is related to the phase of an input "reference" signal [6].Some significant applications are active power filters [7] [8], uninterruptible power supplies [9], power-factor control [10], [11], distributed power generation [12] and flexible ac transmission systems [13]. Synchronous reference frame–phase-locked loops (SRF-s) are the most widely used systems for synchronizing signals [14]. |
| A fast and accurate estimation of fundamental positivesequence component [15] of grid voltage is essential for different applications involving FACTS, power devices and grid connected power converters. It is essential to estimate for both monitoring and control in order to satisfy grid codes, and to obtain high performance response. |
| This paper proposes an enhanced synchronization structure based on PLL and fundamental positive-sequence components which is used to synchronize the component of grid voltages in three-phase systems that can include distorted and asymmetric voltage terms. Finally, the performances of the digital synchronization structure are investigated in the presence of both ideal and non-ideal grid conditions such as amplitude variation, frequency variation, phase jump and improper phase shift. The analysis is carried out in MATLAB/SIMULINK environment and the obtained results are discussed for effectiveness of the study. |
OVERVIEW OF PROPOSED SYSTEM |
| A. Synchronous reference frame based PLL |
| A phase-locked loop is a control system that generates an output signal whose phase is related to the phase of an input "reference" signal [5]. Frequency is the time derivative of phase. Keeping both the input and output phase in lock step implies keeping the input and output frequencies in lock step. Consequently it can track an input frequency or it can generate a frequency that is a multiple of the input frequency. |
| At present Synchronous Reference Frame PLL (SRF-PLL) is the one of the most employed PLL topology. If the single-phase voltage input Vα, is an internally generated signal that is a 90 degrees shifted version of Vβ .The transformation blocks as shown in fig. 1 changes the reference frame, bringing the voltages system from an α-β stationary reference frame to a d-q rotating synchronous reference frame. |
| The feedback loop controls the angular position of this d-q reference frame. In particular the utility voltage vector is totally lined up to the q-axis. In this way it coincides with all its qcomponent; consequently the d-component is made equal to zero. The q-component describes the voltage vector amplitude course. After studying the various Phase Locked Loop schemes used today in modern power system, we observe that the Synchronous Reference Frame PLL method provides a simple yet effective way to measure the phase angle. In case of a single phase system we obtain the quadrature signal by delaying the available sinusoid or adopting some other similar structure, however in 3 phase system this problem is greatly reduced due to the availability of three phase shifted signals. Hence by using arithmetic manipulation we obtain the required orthogonal signal necessary for SRF-PLL implementation. |
| B.Fundamental positive-sequence component: |
| After studying the various Phase Locked Loop schemes used today in modern power system, we observe that the Synchronous Reference Frame PLL method provides a simple yet effective way to measure the phase angle. In this method of digital synchronization structure, the estimation of fundamental positivesequence component is necessary for the rejection of the most relevant disturbances such as voltage imbalance, frequency deviation, phase jumps and improper phase shifts. |
 |
 |
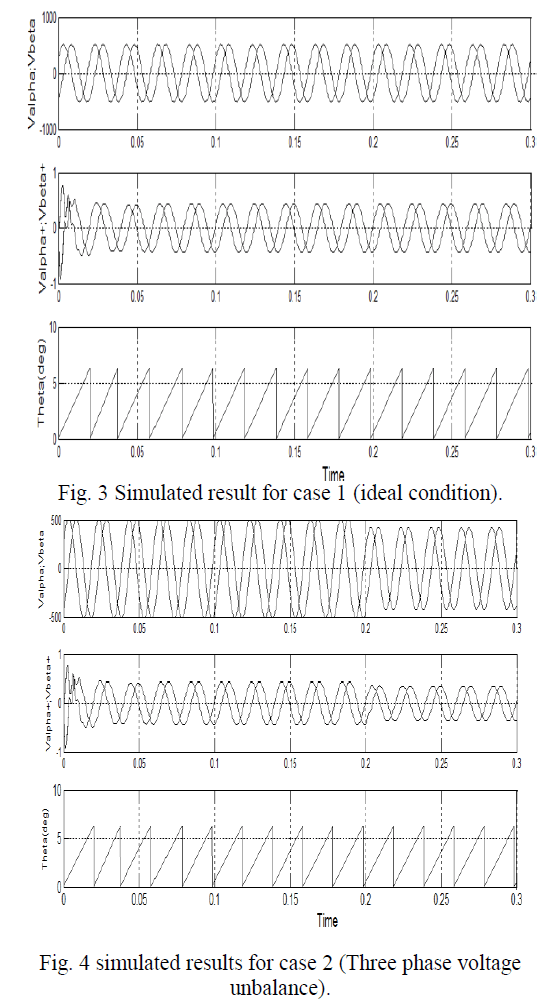 |
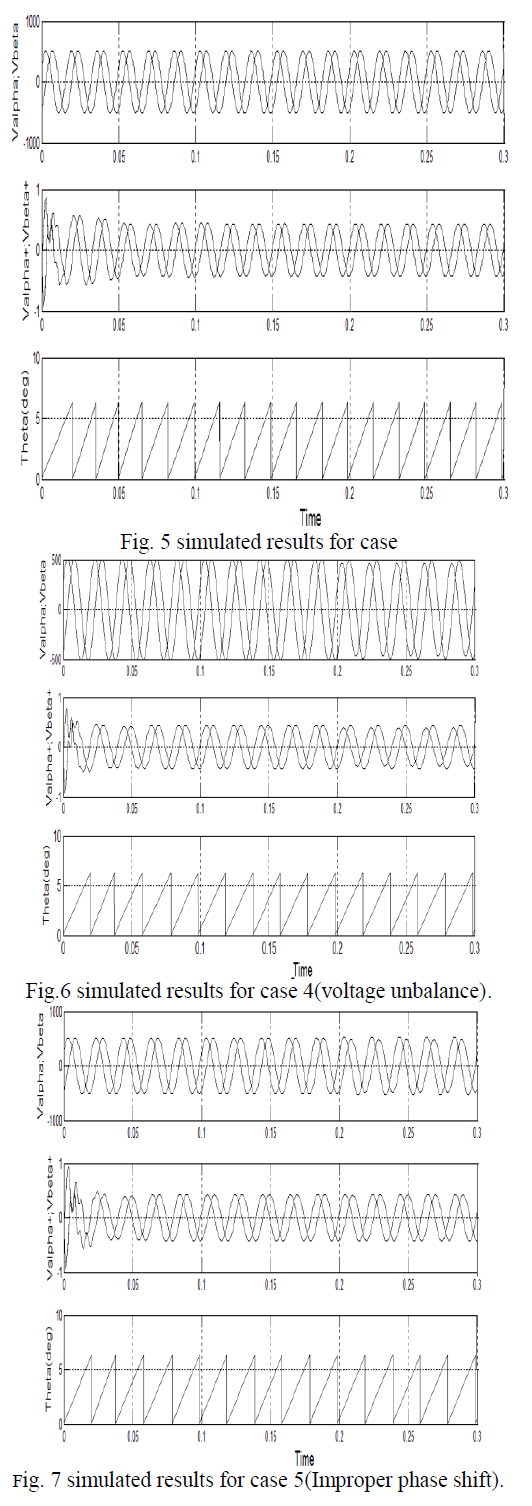 |
| Different non-ideal conditions were simulated and most were handled well by the system. Unbalances in the three phase input signals were overall handled well by the system. The estimation of fundamental positive sequence component and phase angle tracking was performed well by the system. Although the system could handle the non-ideal cases fairly well it was sometimes slow. |
CONCLUSION |
| In the process of synchronization of DG generated power with the utility, phase tracking is very essential for proper grid synchronization. A PLL can be used to obtain magnitude, frequency and phase information for estimation of fundamental positive-sequence component of grid voltage. Accurate and fast estimation of these quantities can be used for control and protection of the system. Overall the grid synchronization system based on positive-sequence estimation is able to handle non-ideal conditions well. The positive-sequence phase angle is tracked within acceptable margins and therefore the PLL system as given with the positive sequence estimation could indeed operate in a real life application. |
ACKNOWLEDGMENT |
| The authors are grateful to the principal and management of K.L.N college of Engineering, Sivagangai for providing all facilities for the research work. |
References |
|