ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
A.S.S. Murugan1, M .A. Jeba Selvam2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
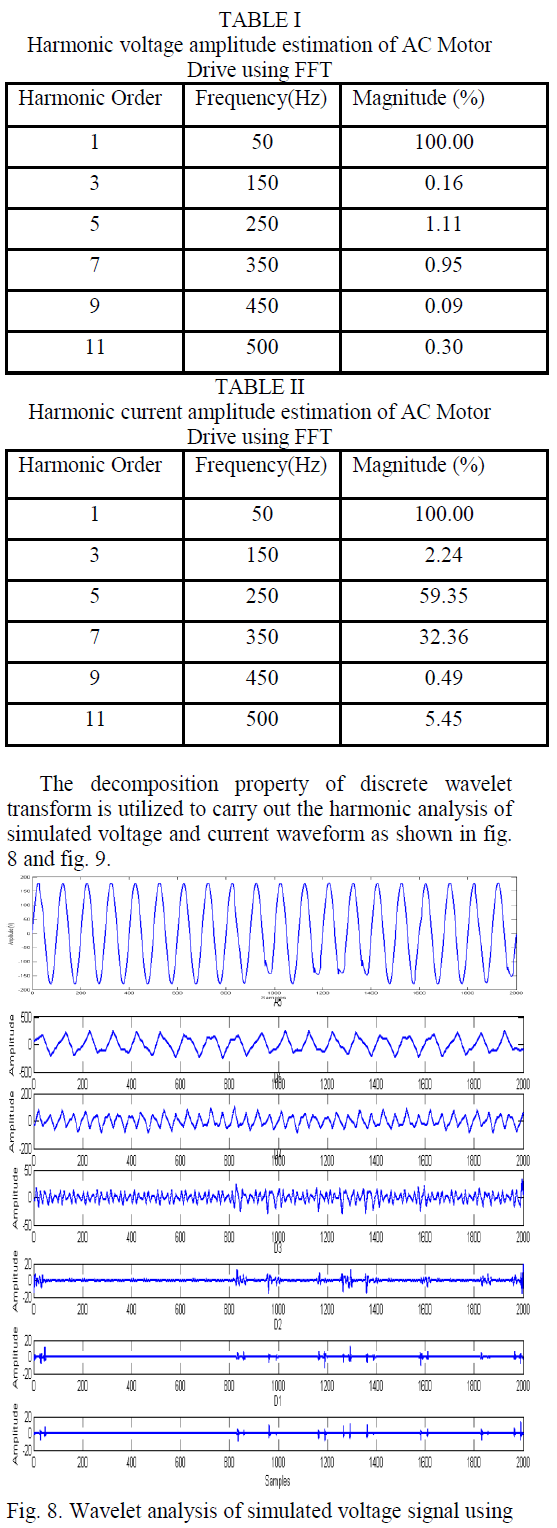
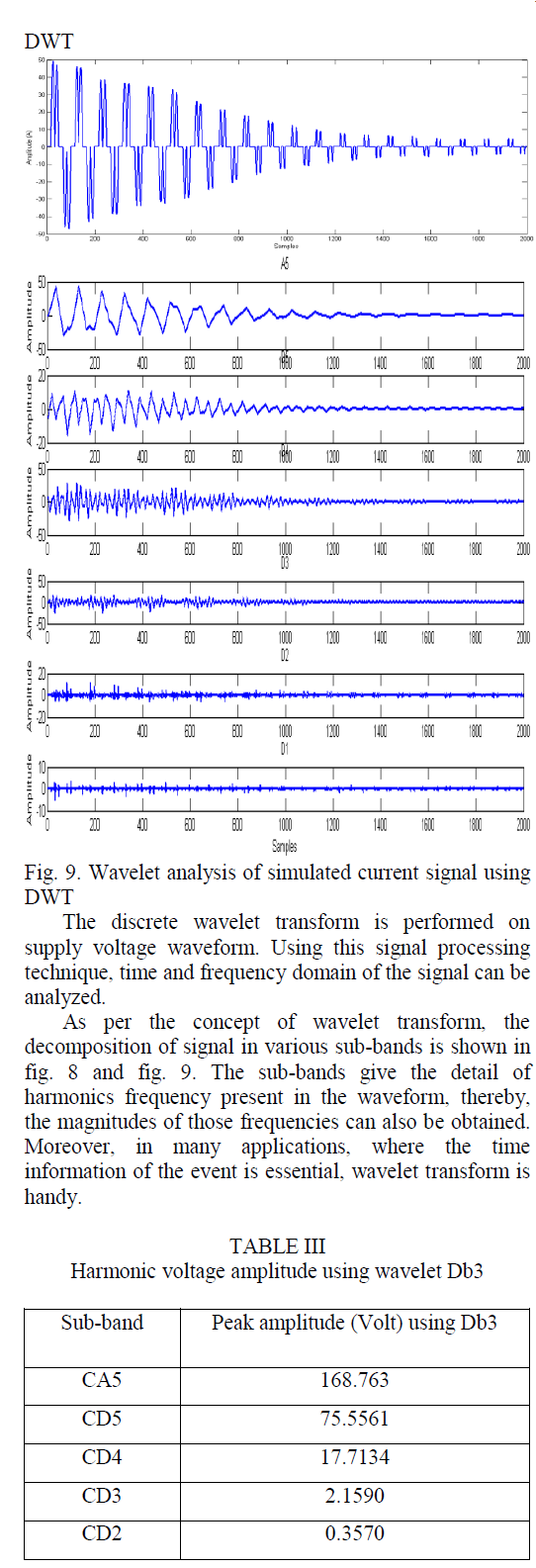
The radical development in the area of power semiconductor switching devices have paved the way for wide use of power electronics based nonlinear loads from industries to the households. In the era of power semiconductor based appliances, defilement in power supply waveform due to harmonics is critical from power quality and reliability point of view. An accurate estimation of harmonics is the basic requirement in the field of harmonic analysis. In this paper, an effective signal processing technique, Discrete Wavelet Transform (DWT) is proposed for the estimation of harmonics in a power system, which is created due to nonlinear loads present. The proposed method is examined with simulated signals of an AC Motor Drive. The method based on Wavelet Transform overcomes the shortcomings of conventional Fast Fourier Transform (FFT) in harmonic estimation.
INDEX TERMS |
| AC Motor Drive, Discrete Wavelet Transform (DWT), Fast Fourier Transform (FFT), Harmonic Estimation, Power Quality |
INTRODUCTION |
| The emphasis on overall power system efficiency in dispersed generation and deregulated electricity market, the quality of power is the increasing concern for both electric utilities and end users of electric power. The increasing use of power semiconductor devices based nonlinear loads such as rectifiers, personal or notebook computers, laser printers, fax machines, dimmers, fluorescent lighting with electronic ballast, stereos, adjustable speed drives, arc furnaces, uninterrupted power supplies, switched-mode power supply (SMPS) equipment, has developed a significant problem of power supply waveform distortion. While there are a few cases where the distortion is random, most distortion is periodic, or an integer multiple of the power system fundamental frequency. This has given rise to the widespread use of the term harmonics to describe distortion of the waveform. |
| Harmonics are sinusoidal voltages or currents having frequencies that are integer multiples of the frequency at which the supply system is designed to operate. Harmonics create numerous problems in the generating and load equipment. Harmonic currents produced by nonlinear loads are injected back into the supply systems. These currents can interact adversely with power system equipment, such as capacitors, transformers, and motors, causing additional losses, overheating, and overloading. These harmonic currents can also cause interference with telecommunication lines and errors in power metering. In addition, harmonics propagate over the system and as a consequence, even linear loads draw harmonic currents from distorted supply. The lower harmonic currents produce less of an impact on other power users sharing the same power lines of the harmonic generating power system. IEEE Standard 519-1992 represents a consensus of guidelines and recommended practices by the utilities and their customers in minimizing and controlling the impact of harmonics generated by nonlinear loads. |
| An accurate estimation of harmonics is required in designing harmonic filters, and for other harmonic pertained issues. The Fourier transform consents a very convenient assessment of magnitude and phase information. It is an efficient algorithm for spectral analysis, which requires low computation time; nevertheless, it suffers shortcomings resulting in inaccuracies. Recent literature [3]-[5] employs countermeasures, such as interpolation, windowing, and harmonic grouping, in order to avoid pitfalls of fast Fourier transform. But those measures come at the expense of additional computational burden. This paper proposes a method grounded on Wavelet Transform. The Discrete Wavelet Transform (DFT) is accounted as a well suited execution for harmonic group estimation in accordance with IEC Standard 61000-4-7 [2]. It is a signal decomposition technique, which is useful in separating frequency components. The simulated signals are used to validate the proposed wavelet transform. |
DISCRETE WAVELET TRANSFORM |
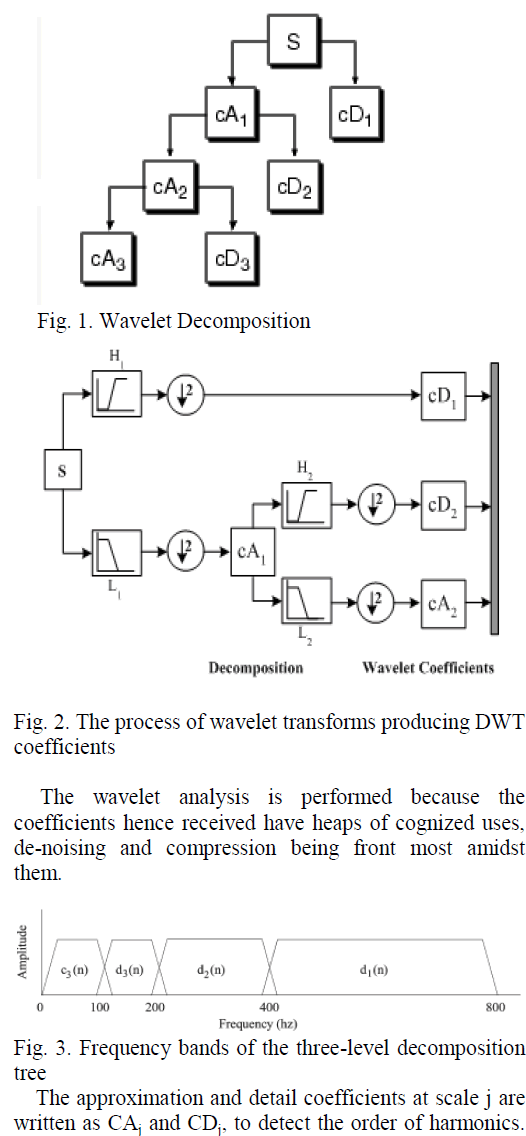
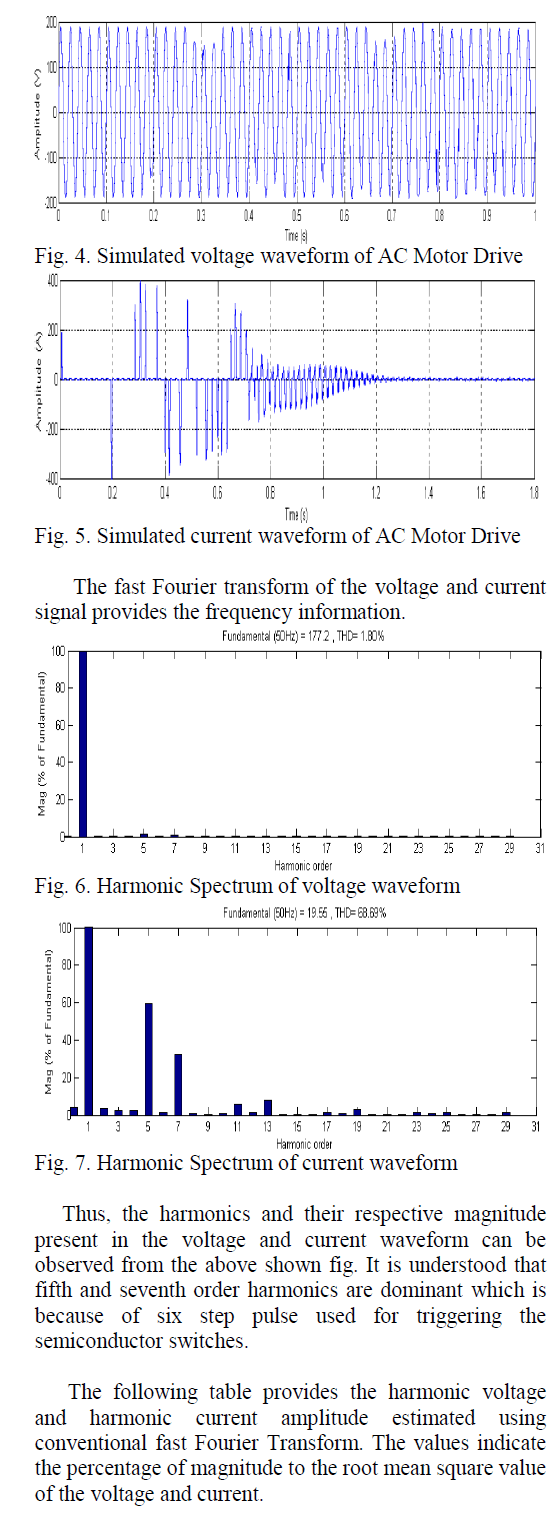
| A wavelet is a waveform of efficaciously limited duration that has an average value of zero. Wavelet transform is adequate to provide the time and frequency information simultaneously, thus yielding a better timefrequency representation of the signal than any other existing transforms. In wavelet analysis, approximations and details are the terms used. The discrete wavelet transform can be defined as a mathematical tool in which the original signal is passed through two complementary filters and comes forth as two signals known as approximations and details. The approximations are the high-scale, low-frequency components of the signal. The details are the low-scale, high-frequency components. The wavelet transform uses short windows at high frequencies and long windows at low frequencies. This results in multi resolution analysis by which the signal is analyzed with different resolutions at different frequencies. |
 |
 |
 |
 |
 |
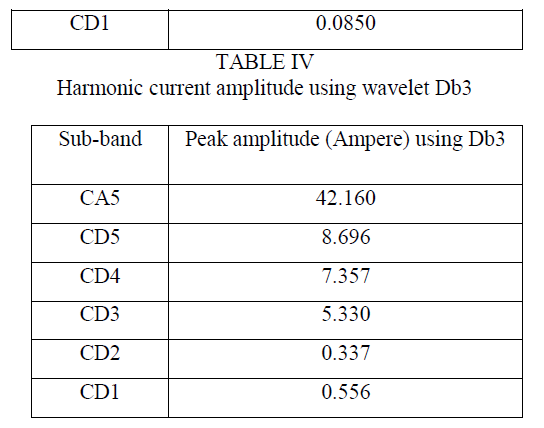 |
CONCLUSION |
| This paper presents the harmonic amplitude assessment of voltage and current signal of simulated AC Motor Drive. The estimation of harmonics in the power system forms the basis in the field of harmonic analysis. The accuracy and computational complexity are two main features that determine the effectiveness of any harmonic estimation technique. The conventional fast Fourier transform is simple and accurate in the absence of frequency deviation and interharmonics. The signal processing technique, wavelet transform, overcomes the shortcomings of conventional method used for harmonic analysis. |
References |
|