ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
G.Mohana Prabha, E.Balraj
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A novel Ant Colony Optimization algorithm (ACO) combined for the hierarchical multi- label classification problem of protein function prediction. This kind of problem is mainly focused on biometric area, given the large increase in the number of uncharacterized proteins available for analysis and the importance of determining their functions in order to improve the current biological knowledge. Because it is known that a protein can perform more than one function and many protein functional-definition schemes are organized in a hierarchical structure, the classification problem in this case is an instance of a hierarchical multilabel problem. In this classification method, each class might have multiple class labels and class labels are represented in a hierarchical structure—either a tree or a directed acyclic graph (DAG) structure. A more difficult problem than conventional flat classification in this approach, given that the classification algorithm has to take into account hierarchical relationships between class labels and be able to predict multiple class labels for the same example. The proposed ACO algorithm discovers an ordered list of hierarchical multi-label classification rules.
INTRODUCTION |
| Classification is one of the important d a t a mining tasks. The main objective of this is to learn a relationship between input values and a desired output. A set of examples defined by a classification problem, where each example is explained by predictor attributes and associated with a class attribute. It consists of two phases. F irst phase consists of g i v e n a labeled data set—a data set consisting of examples with a known class value (label) as an input, a classification model that represents the relationship between predictor and class attribute values is built. The second phase, the classification model is used to classify unknown examples— examples with unknown class value. |
| Most of the classification algorithms are discussed in the previous algorithms, each example is associated with only one class value or label and class values are unrelated—i.e. there are no relationships between different class values. The above said classification problems are usually referred to as flat (nonhierarchical) single-label problems. The main problem of hierarchical multi label classifications are, examples may be associated to multiple class values at the same time and the class values are organized in a hierarchical structure (e.g. a tree or a directed acyclic graph structure). According to the data mining perspective, hierarchical multi-label classification is more challenging than flat single-label classification. Most difficult task of hierarchical multi label classification is to discriminate between classes represented by nodes at the bottom of the hierarchy than classes represented by nodes at the top of the hierarchy, since the number of examples per class tends to be smaller at lower levels of the hierarchy as opposed to top levels of the hierarchy. Another problem is, class predictions must satisfy hierarchical parent-child relationships, since an example associated with a class is automatically associated with all its ancestors’ classes. F i n a l p r o b l em i s , multiple unrelated classes— classes which are not involved in ancestor/descendant relationship may be predicted at the same time. |
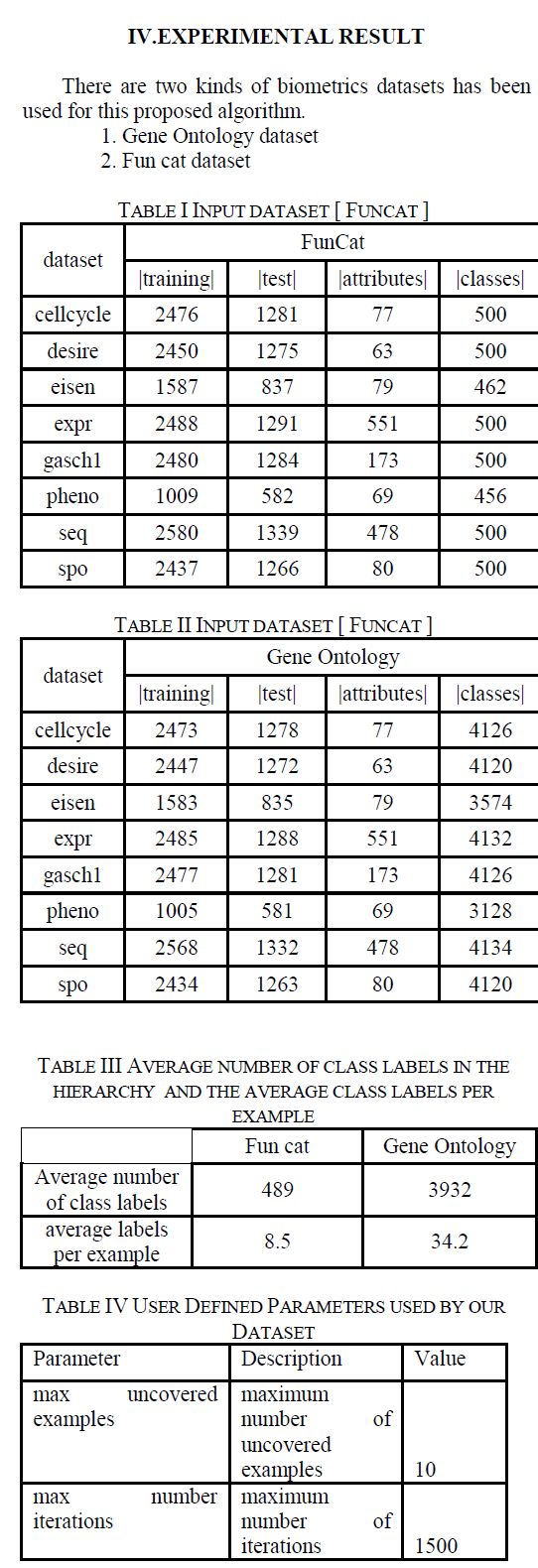
| There has been an increasing interest in hierarchical classification, where in general early applications are found in text classification and recently in protein function prediction .The latter is a very active research field, given the large increase in the number of uncharacterized proteins available for analysis and the importance of determining their functions in order to improve the current biological knowledge. It is important to emphasize that in this context, comprehensible classification models which can be validated by the user are preferred in order to provide useful insights about the correlation of protein features and their functions. Concerning the problem of protein function prediction, the focus of we, an example to be classified corresponds to a protein, predictor attributes correspond to different protein features and the classes correspond to different functions that a protein can perform. Since it is known that a protein can perform more than one function and function definitions are organized in a hierarchical structure (e.g. FunCat and Gene Ontology protein functional-definition schemes), the classification problem in this case is an instance of a hierarchical multi-label problem. |
LITERATURE SURVEY |
| Ant Colony Optimization |
| Ant Colony Optimization algorithms simulate the behavior of real ants using a colony of artificial ants, which cooperate in finding good solutions to optimization problems. Every artificial ant, representing a simple agent, builds candidate solutions to the problem at hand and communicates indirectly with other artificial ants by means of pheromone values. At the same time that ants perform a global search for new solutions, the search is guided to better regions of the search space based on the quality of solutions found so far. The algorithm converges to good solutions as a result of the collaborative interaction among the ants; an ant probabilistic chooses a trail to follow based on heuristic information and pheromone values, deposited by previous ants. The interactive process of building candidate solutions and updating pheromone values allows an ACO algorithm to converge |
| MuLAM Optimization |
| It proposed a new ACO algorithm, named MuLAM (Multi-Label Ant-Miner), for discovering multi-label classification rules. In essence, MuLAM differs from the original Ant-Miner in three aspects, as follows. Firstly, a classification rule can predict one or more class attributes, as in multi-label classification problems an example can belong to more than one class. Secondly, each iteration of MuLAM creates a set of rules instead of a single rule as in the original Ant-Miner. Thirdly, it uses a pheromone matrix for each class value and pheromone updates only occur on the matrix of the class values that are present in the consequent of a rule. In order to cope with multi-label data, MuLAM employs a criterion to decide whether one or more. |
| hAnt Miner |
| This Algorithm proposed an extension of the flat classification Ant-Miner algorithm tailored for hierarchical classification problems, named hAnt-Miner (Hierarchical Classification Ant-Miner), employing a hierarchical rule evaluation measure to guide pheromone updating, a heuristic information adapted for hierarchical classification, as We as an extended rule representation to allow hierarchically related classes in the consequent of a rule. However, hAnt-Miner cannot cope with hierarchical multi-label problems, where an example can be assigned to multiple classes that are not ancestor/descendant of each other. |
EXISTING SYSTEM |
| hAnt-Miner algorithm is the discovery of hierarchical classification rules in the form IF antecedent THEN consequent. The antecedent of a rule is composed by a conjunction of conditions based on predictor attribute values (e.g. length > 25 AND IPR00023 = yes) while the consequent of a rule is composed by a set of class labels in potentially different levels of the class hierarchy respecting ancestor/decendant class relationships (e.g., GO:0005216, GO:0005244—where GO:0005244 is a subclass of GO:000-5216). This algorithm divides the rule construction process into two different ant colonies, one colony for creating antecedent of rules and one colony for creating consequent of rules, and the two colonies work in a cooperative fashion. |
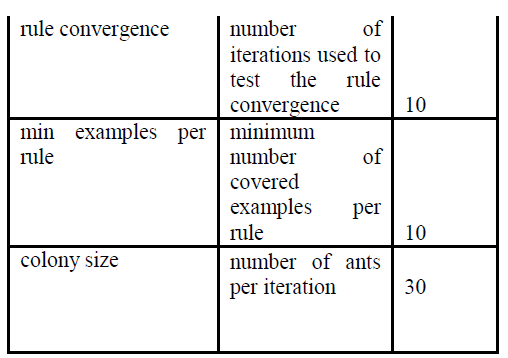
| Af t e r the rule construction procedure has finished, the rules constructed by the ants are pruned to remove irrelevant terms (attribute-value conditions) from their antecedent— which can be regarded as a local search operator—and class labels from their consequent. Then, pheromone levels are updated using the best rule (based on a quality measure Q) of the current iteration and the best-so-far rule (across all iterations) is stored. The rule construction procedure is repeated until a user-specified number of iterations has been reached, or the best-so-far rule is exactly the same in a predefined number of previous iterations. The bestso- far rule found is added to the rule list and the covered training examples—i.e. examples that satisfy the rule’s antecedent conditions—are removed from the training set. |
| Overall, hAnt-Miner can be regarded as a memetic algorithm, in the sense that it combines conventional concepts and methods of the ACO meta heuristic with concepts and methods of conventional rule induction algorithms (e.g. the sequential covering and rule pruning procedures), as discussed earlier. |
| According to discover a list of classification rules, a sequential covering approach is employed to cover all (or almost all) training examples. Algorithm 1 presents a high- level pseudo code of the sequential covering procedure employed in hAnt-Miner. |
 |
 |
| PROBLEM DESCRIPTION |
| While analyzing hAnt-Miner, We have identified the following limitations. |
| The main drawback of the hAntMiner is heuristic information, which involves a measure of entropy, used in hAnt-Miner is not very suitable for hierarchical classification—i.e. it will not consider for identifying the hierarchical relationships between classes. Even though hAnt-Miner’s entropy measure is calculated throughout all labels of the class hierarchy (apart from the root label), each class label is evaluated individually without considering parent-child relationships between class labels. |
| Another drawback is, the measurement of rule quality is prone to over fitting. Because only the examples covered by the rule are considered in the rule evaluation, rules with a small coverage are favoured over more generic rules. Let We consider the example, the class label 1.2.1 with 20 examples and two rules that have class 1.2.1 as the most specific class label in their consequent: rule1 covering correctly 5 examples out of a total of 5 covered and rule2 covering correctly 19 examples out of a total of 20 covered. According to this situation, rule1 would have a higher quality, because all the examples covered by the rule are correctly classified, than rule2, which misclassifies one ex- ample, though rule2 covers all but one examples belonging to class 1.2.1. I mp o r t a n t i s s u e that the rule quality mea- sure of hAnt-Miner could be easily modified to avoid over- fitting by evaluating a rule considering all the examples of its most specific class. The drawback of this approach is that it favors rules predicting class labels at the top of the hierarchy, since the numbers of examples per class are greater at top class levels. This could potentially prevent the discovery of rules predicting more specific class labels given that the examples covered by a rule are removed from the training set—indeed; this problem was observed in some preliminary experiments. |
| At last, I t does not support multi-label data since a single path in the consequent construction graph corresponds to the consequent of a rule. I f We take protein function prediction, where it is known that a protein can perform more than one function. So it also considered as one of the important issue . |
PROPOSED WORK |
| A new hierarchical multi-label ant colony classification algorithm, named hmAnt-Miner (Hierarchical Multi-Label Classification Ant-Miner) is developed to overcome the aforementioned limitations. E v e n hmAnt-Miner shares the same underlying procedure of the hAnt-Miner algorithm as We have seen, it differs from hAnt-Miner in the following aspects: |
| The consequent of a rule is evaluated using a deterministic procedure based on the examples covered by the rule, allowing the creation of rules that can predict more than one class label at the same time (multi-label rules). Therefore, hmAnt-Miner uses a single construction graph in order to create a rule—only the antecedent is rep- resented in the construction graph; |
| Euclidean distance is used to define the heuristic function, where each example is represented by a vector of class membership values in the Euclidean space. I ns t e ad o f u s i ng e nt ro p y in hAntMi ne r We c an u s e d i s t a nc e me a s ur e he lp u s to id ent i fy possible to take into account the relationship between class labels given that examples belonging to related (ancestor/decendant) class labels will be more similar than examples belonging to unrelated class labels. This concept is inspired from C LU S -HMC algorithm for hierarchical multi-label classification, it i s based on the paradigm of decision tree induction, rather than rule induction. |
| A distance based measure can be used to evaluate the rule quality, which is a more suitable evaluation measure for hierarchical multi-label problems; |
| Rule pruning procedure is not applied to the consequent of a rule. It is (re-)calculated when its antecedent is modified during pruning, since the set of covered examples might have changed |
| The Consequent Rule Construction |
 |
| entropy characterizes the homogeneity of a collection of examples related to the class attribute values, giving a notion of (im-)purity of the class values’ distribution. The more examples of the same class the lower the value of entropy will be and the ‘purest’ is the collection of examples. It should be noted that in all calculations involving entropy, the different class labels (values) are independently evaluated—i.e. no relationship between class labels is taken into account. In the case of Ant- Miner, which is applied to flat classification problems, the use of the entropy measure does not present a limitation, since there is no relationship between class labels. On the other hand, the same cannot be said for hAnt-Miner, which aims at extracting hierarchical classification rules, derived from data where the class labels are organized in a hierarchical structure |
| To illustrate the limitation of the entropy measure when used in hierarchical problems, let us consider the following example. Given a tree-structured class hierarchy, where labels {1, 2, 3} are children of the root label and labels {2.1, 2.2} are children of the ‘2’ label and each class label has 10 examples. Although the entropy is calculated according to Equation (4)— across all class labels, the hierarchical relationships are not taken into account. Therefore, the entropy of a hypothetical term ‘IPR00023 = yes’ which is present in 10 examples of class ‘1’ and in 10 examples of class ‘3’ would be the same as of a hypothetical term‘IPR00023 = no’ which is present in 10 examples of class‘2’ and in 10 examples of class ‘2.1’. The drawback in this case is that it is known that class labels ‘2’ and ‘2.1’ are more similar than class labels ‘1’ and ‘3’. Hence, it would be expected/desired that the entropy measure (or an alternative heuristic information) exploit hierarchical relationships in order to better reflect the quality of each term in the case of hierarchical classification problems. Intuitively this becomes even more important when dealing with bigger (in terms of number of class labels and depth) hierarchical structures. It should be noted that several Ant-Miner variations—as dis- cussed have used a heuristic information based on the relatively frequency of the class predicted by the rule (or the majority class) among all the examples that have a particular term, which would also present the above limitation. |
| hmAnt-Miner employs a distance-based heuristic information, which directly incorporates information from the class hierarchy. More precisely, the heuristic information of a term corresponds to the variance of the set of examples covered by the term (the set of examples that satisfy the condition represented by the term). In order to calculate the variance, the class labels of each example are represented by a numeric vector of length m (where m is the number of class labels of the hierarchy without considering the root label). The i-th component of the class label vector of an example is equal to 0 or 1 if the correspondent class label is absent or present, respectively. The distance betWeen class label vectors is defined as the Weighted Euclidean distance, given by |
 |
 |
 |
 |
CONCLUSION |
| The proposed paper presents a novel ant colony algorithm tailored for hierarchical multi-label classification, named hmAnt- Miner (Hierarchical Multi- Label Classification Ant-Miner). Extending on the ideas of our previous hierarchical classification hAnt-Miner algorithm, hmAnt-Miner discovers a single global classification model, in the form of an ordered list of IF-THEN classification rules, which can predict all class labels from a class hierarchy at once, and examples may be assigned to multiple unrelated class labels. On account of the information from the class hierarchy, hmAnt-Miner employs a distance-based measure in the dynamic discretization procedure of continuous attributes and as heuristic information in the ACO construction graph. Because of that, the entropy measure used in hAnt-Miner is replaced by the distance measure in hmAnt-Miner, which is a more suitable measure for hierarchical multi-label classification. |
| Our proposed work have conducted experiments comparing hmAnt-Miner against state-of-the-art decision tree induction algorithms for Hierarchical multi-label classification with most challenging sixteen bioinformatics data sets involving the prediction of protein function, with large numbers of predictor attributes and large numbers of class labels to be predicted. Class hierarchies Were used in the experiments are represented in a tree (where a class label has a single parent, apart from the root label) or in a directed acyclic graph (where a class label can have multiple parents, apart from the root label) forms. We assure that hmAnt-Miner is most competitive in term of both predictive accuracy and simplicity We regard these results promising, given that hmAnt-Miner is the first ACO algorithm tailored for hierarchical multi-label classification, to the best of our knowledge. |
References |
|