ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Kajal K. Patel1, M. N. Mehta2, Twinkle R. Singh3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The Homotopy analysis method has been applied to Richard's equation under considering the value of diffusivity coefficient Dï±  and hydraulic conductivity Kï±  under certain assumption. The solution of this equation has been obtained by considering the guess value of pressure head in an unsaturated soil. It is concluded that the pressure head in an unsaturated soil is decreasing as depth Z is increasing for given time T > 0. The graph and a numerical value are given by using Maple coding
Keywords |
| Richard's equation, Unsaturated porous media, Homotopy Analysis Method, Infiltration Phenomenon. |
I. INTRODUCTION |
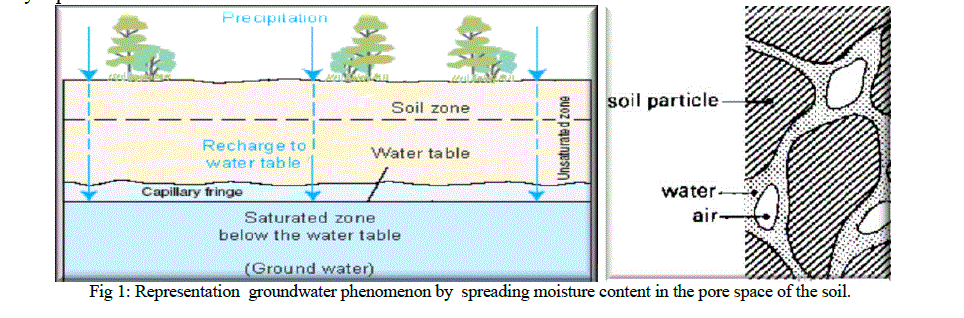
| From last few years, groundwater flow and mass transport in the unsaturated porous media has significantly increasingly and it has a great important for hydrologist, agriculturists and people related with water resources sciences. In hydrology, volumetric water content is very important phenomenon in infiltration of groundwater in an unsaturated porous media. The groundwater flow and mass transport in the unsaturated porous media is a region of underground as its top by the soils (porous media) and below by the groundwater table, where physical phenomena such as infiltration, groundwater recharge, moisture content and others are happened. Ground water recharge problem has been discussed by many researchers with different viewpoints. Swartzendruber uses Philip’s [31] method to get graphical illustration of the mathematical solution for horizontal water function. Verma and Mishra [29] have obtained solution by similarity transformation of a unidimensional vertical ground water recharges through porous media. Mehta [27] has obtained an approximate solution by the method of singular perturbation technique. Hari Prasad et al. [30] had developed a numerical model for unsaturated zones for the process of gravity drainage and infiltration. Almost all unsaturated flow simulations use the Richard's equation. Richards [15] investigated the influence capillarity has on liquid infiltration in soils, and equation derived is now known as Richards' equation. He derived a governing nonlinear equation for water flow in porous media based on a continuum approach. In the derivation of Richards' equation, it is assumed the liquid infiltration is driven by capillarity and gravity, while the second fluid phase occupying the unsaturated void-spaces is largely inert and does not affect the evolution. The sophistication of the analytical and numerical methods that are available for solving the governing nonlinear equation of unsaturated flow in porous media (Richard's Equation) require specialized forms of the conductivity (hydraulic conductivity) and water diffusivity (diffusivity functions). Several investigators have described different relation between the diffusivity coefficient and hydraulic conductivity in groundwater recharge problem. |
| In 1958, Gradner [32] model provided a relationship between the pressure head 'h' and the volumetric water content as, b h a where a & b are empirical constants. The exponential hydraulic conductivity function has been widely used, but it is known to have a limited range of application to many real soils. Other functions developed by Brooks and Corey [33] and Van Genuchten [31] are firmly established for practical applications. Such special forms of the hydraulic functions make it possible to linearize the governing flow equations, and hence solve them analytically. Solutions to the linearized unsaturated flow equations are generally limited to the steady flow in semi-infinite, homogenous soils (Broadbridge and White, 1988; Warrick and Yeh, 1990) and to transient flow in homogeneous and layered soils (Srivastava and Yeh) [7]. In 1988,The Broadbridge and White Model [5] has adopted a function form for the diffusivity given by Philip and Knight (1974)[6] which allows for the transformation of the soil water diffusivity D as function has the form: |
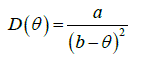 |
| conditions, the Hopf-Cole transformations are applied to reduce a nonlinear equation to a linear form that possesses an exact parametric solution [5]. In this paper, Broadbridge and White Model [5] was applied to solve infiltration phenomenon in unsaturated porous media. In 1992, Liao[12] employed the basic idea of the homotopy in topology to propose a general analytical method for nonlinear problems, namely Homotopy Analysis method. Homotopy analysis method has been applied to nonlinear fluid dynamics problems by Liao [9], [11]. The important factor of this method is the generalized Taylor expansion. Liao point out that the generalized Taylor series provided a way to control and adjust the convergence region through an auxiliary parameter such that this method is particularly suitable for strongly nonlinear problems. This method does not dependence on small or large parameter and is easy to adjust the convergence region and rate of approximation of the series. In this paper, ground water recharge phenomenon is solved by Homotopy analysis method. |
| II. ASSUMPTION AND MATHEMATICAL STATEMENT OF THE PROBLEM |
| In the present model, Darcian-based unsaturated flow equation described over the large basin L (i.e. L is the length of a large basin) of homogeneous porous media, and there is no air resistance to the flow (i.e. the porous medium contains only the flowing liquid water and empty voids of air). The air in the void space is approximately at atmospheric pressure. The flowing liquid (water) is considered continuous at a microscopic level, incompressible and isothermal, where the pressure head in unsaturated soil is considered as time depended function. In this case consider the flow of infiltrated water in vertical downward direction up to length L by neglecting spreading in other directions. We obtain one dimensional nonlinear partial differential equation by combining Darcy's law [1] for unsaturated flow with the continuity equation. |
 |
| In this paper, the Homotopy analysis method is implemented to obtain the approximate solutions of the governing nonlinear partial second order differential equation for infiltration phenomenon, which is able to solve the onedimensional h-based forms of Richard's equation. Its solution provides the infiltrated water into the porous media (soil) at any depth Z at time T > 0. The graph of pressure head versus time T is given at depth Z > 0, which shows at any depth Z pressure head is decreases as time T increases. |
III. MATHEMATICAL STRUCTURE |
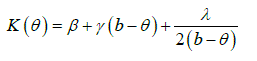 |
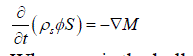 |
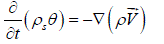 |
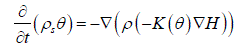 |
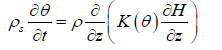 |