ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
P.Arunpriya1, S.Rinesh2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Large-scale image data sets are being exponentially generated today. Along with such data explosion is the fast growing trend to outsource the image management systems to the cloud for its abundant computing resources and benefits. How to protect the sensitive data while enabling outsourced image services, however, becomes a major concern. Earlier method used compressed sensing for image reconstruction purpose. In that, it supports only typical sparse data acquisition and reconstruction in standard compressed sensing context. However, dense component of image is not considered. In order to provide the correlation of dense and sparse signal of the image we propose a correlated compressed sensing algorithm. This algorithm takes an advantage of the correlation between dense and sparse components of the signal in the recovery procedure at the image decoder side. In this way, we are able to reduce the number of measurements and computation time while obtaining the same accuracy.
Keywords |
| Correlated compressed sensing, security, privacy, cloud computing, image reconstruction. |
INTRODUCTION |
| The advancement of information and computing technology, wide range datasets are being exponentially generated nowadays. Examples under various application contexts include medical images, remote sensing images, satellite image databases, etc. Along with such data explosion is the fast-growing vogue to outsource the image management systems to cloud and leverage its economic yet lavish computing resources to efficiently and effectively acquire, store, and share images from data owners to a large number of data users .Although in order to become truly successful, it still faces a number of fundamental and critical challenges, among which security is the top item. This is due to the fact that the cloud is an open environment operated by external third parties who are usually outside of the data owner/users' trusted domain. On the other hand, many image datasets, e.g., the medical images with diagnostic results for different patients, are privacy-sensitive by its nature. Thus, it is of critical importance to ensure that security must be embedded in the image service outsourcing design from the very beginning. |
| Reconstructing images from compressed samples requires solving an optimization problem; it can be burdensome for users with computationally weak devices, like tablets or large-screen smart phones. OIRS aims to shift such expensive computing workloads from data users to cloud for faster image reconstruction and less local resource consumption, yet without introducing undesired privacy leakages on possibly sensitive image samples or the recovered image content.More than that we need to do more number of measurements and mathematical calculations. In that, it supports only typical sparse data acquisition and reconstruction in standard compressed sensing context. However, dense component of image is not considered. In order to provide the correlation of dense and sparse signal of the image we propose a correlated compressed sensing algorithm. This algorithm takes an advantage of the correlation between dense and sparse components of the signal in the recovery procedure at the image decoder side. In this way, we are able to reduce the number of measurements and computation time while obtaining the same accuracy. To meet these challenging requirements, a core part of the OIRS design is a tailored light weight problem transformation mechanism, which can help data owner/user to protect the sensitive data contained in the optimization problem for original image reconstruction and to reduce the number of measurements. |
ALLIED WORK |
| Correlated compressed sensing is a new image representation method, which is different from the previous works oncompressive imaging, which treat the whole image as a compressible signal, here we decompose an image into two components: a dense component and a sparse component. The decomposition helps to generate a sparser signal which is proved more suitable for Compressed Sensing. The proposed algorithm takes advantage of the correlation between dense and sparse components of the signal in the recovery procedure at the image decoder side. . The idea is to store the compressed image samples on behalf of the whole image, either in compressed or uncompressed format, on storage servers. Their results show that storing compressed samples offers about 50% storage reduction compared to storing the original image in uncompressed format or other data application scenarios where data compression may not be done. But their work does not consider security in mind, which is an indispensable design requirement in correlated compressed sensing.In fact, compared to that only focuses on storage trim down, our proposed correlated compressed sensing method aims to achieve a much more ambitious goal, which is an outsourced image service platform and takes into consideration of security, efficiency, effectiveness,and complexity from the very beginning of the service flow with the help of OIRS. |
PROBLEM STATEMENT |
| A. Service model and threat model |
| The basic service model in the OIRS architecture includes the following: At first, data owner acquires raw image data, in the form of compressed image samples, from the physical world under different imaging application contexts. To trim down the local storage and maintenance overhead, data owner later outsources the raw image samples to the cloud for storage and processing. The cloud will on-demand reconstructs the images from those samples upon receiving the requests from the users. In our model, data users are assumed to possess mobile devices with only limited computational resources. |
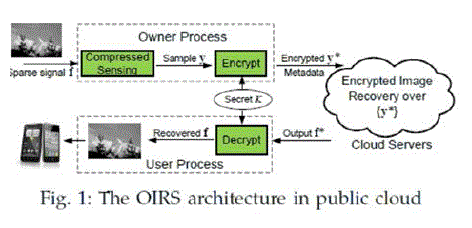 |
| We consider a semi-trusted cloud as the adversary in OIRS. The cloud is assumed to honestly perform the image reconstruction service as specified, but be curious in learning owner/user's data content. Because the images samples captured by data owners usually contain data specific/sensitive information, we have to make sure no data outside the data owner/user's process is in unprotected format. |
| B. Design goals |
| Our design goals for OIRS under the aforementioned service and threats model consist of the following. |
| Security: OIRS should provide the strongest possible protection on both the private image samples and the content of the recovered images. |
| Effectiveness: OIRS should enable cloud to effectively perform the image reconstruction service over the encrypted samples. |
| Efficiency: OIRS bring savings from the computation and/or storage aspects to data owner and users. |
| Extensibility: In addition to image reconstruction service, OIRS should be made possible to support other extensible service interfaces and even performance speedup via hardware built-in design. |
CORRELATED COMPRESSED SENSING |
 |
OIRS DESIGN |
| While compressed sensing simplifies the data acquisition at data owner, it makes the data recovery from the compressed samples a computationally intensive task. As introduced in the preliminary, it requires the data users to solve an optimization problem, which could be very challenging for the data user with computationally weak devices like smart phones. Therefore, enabling a secure data recovery service by leveraging the cloud is of critical importance in our proposed OIRS architecture. Due to the sensitive nature of data, to outsource compressed image samples directly to the cloud is prohibited. And we need to protect the image samples before outsourcing them to the cloud. The cloud should not be able to learn the private content of the image samples either before or after the image reconstruction. |
| Framework and security definitions of OIRS |
| Given the problem formation for image reconstruction in Section III-C,our design challenge in OIRS is how to let the cloud efficiently solve the optimization problem, Ω= D (F; y; I; 1T), for image reconstruction without learning content of either compressed image samples y or the reconstructed image data g. To meet these design challenges, |
| Definition 1: A transformation scheme ᴦ = D(KeyGen, ProbTran, ProbSolv, DataRec) is secure if |
| ∀Ω0,Ω1 : Pr[K←keyGen(1k):ProbTran(K,Ω0)=Ωk] -Pr[K←keyGen(1k):Probtran(K,Ωk]≤μ whereμ is a negligible function. |
| From the perspective of in distinguish ability, such a security formulation is also loosely related to the general formulation of differential privacy [15], [16]. |
| The blueprint of problem transformation According to our framework and security definition, the purpose of ProbTran is to transform Ω into a random Ωk where the latter shares the same problem structure as the former, y and F are supposed to be protected against the cloud, while I and 1Tare public information. Thus, the challenge of the transformation based design is that we have to ensure such public information will not be maliciously leveraged by the cloud to tamper the overall protection of OIRS. |
| 1) We use a random generalized permutation matrix π with positive entries, i.e., the product of a non-zero positive diagonal and a permutation matrix, to rewrite the inequality constraints. |
| min1T. g |
| y = F .g, π . g≥0. |
| Note that π.g ≥ 0 is equivalent to g ≥ 0. |
| 2) We randomly pick a 2n x 2n invertible matrix Q and a 2n x 1 vector e to protect the solution g via af_ne mapingg = Qh– e. |
| min1T.(Qh- e) |
| subject to F.Q . h = y + F .e; |
| π.Q .h ≥ π.e. |
| 3) We multiply a random 2n x mmatrix M to equality constraints |
| and later mix the result together with the inequality constraints |
| min1T. (Qh- e) |
| subject to F . Q .h = y + F .e; |
| This problem is equivalent to the one in Step 2 |
| 4) We multiply a random m_minvertible matrix P to the both sides of equality constraints |
| min1T. (Qh- e) |
| subject to PFQ . h = P . (y + F .e). |
| The scheme details |
| Scheme details: Based on the above one, we describe the complete protocol for the OIRS framework ᴦ. |
| Algorithm 1 Key Generation |
| Data: security parameter 1k ,random coins σ |
| Result: K D (P;Q; e; π;M) |
| % discussion on choice of k deferred in Section V; |
| begin |
| 1 uses σ to generate random P; e; π; |
| 2 usesσ to generate random Q and M; |
| % satisfying the structure of Ωk in Prob. 5 |
| 3 return secret key K = (P;Q; e; π;M) ; |
| Algorithm 2 Problem Transformation Step 1 |
| Data: transformation key K and original LP Ω |
| Result: protected sample y’ in Ωk |
| begin |
| 1 picks P; e from K and F from Ω; |
| 2 return y’ = P . (y + F .e) ; |
| Algorithm 3 Problem Transformation Step 2 |
| Data: transformation key K and original LP Ω |
| Result: protected coefficient matrices F’,π′ in Ωk |
| begin |
| 1 picks (P;Q; π;M) in K and F in Ω; |
| 2 computes F’= PFQ and = (π- MF)Q; |
| 3 return transformed F’,π′; |
| Algorithm 4 Original Answer Recovery |
| Data: transformation key K and protected answer h of Ωk |
| Result: answer g of original problem Ω |
| begin |
| 1 picks Q; e from K; |
| 2 return g = Qh- e ; |
| Data sampling phase |
| 1) Data owner picks a fresh seed and generates a secret key K = (P,Q,e,π,M) |
| 2) He acquires the sample y = Rx = RVf= Af to cloud |
| We assume the samples and the related seeds fy’; sg are all stored in an authenticated manner at cloud. Assume that data user issues an image recovery request for an image sample y’ to data owner. |
| Image recovery phase |
| 1) Data owner downloads the seed s from cloud, computesF(sk; s), and uses σ to regenerate the matrix R and the key K D (P;Q; e;M) from KeyGen.He calls ProbTran2(K; F) to get (F0; _0) and sends them to cloud. |
| 2) With Ωk= (F’; π′; y’;1T), the cloud calls ProbSolv (Ωk ) to output answer h to user, together with seeds. |
| 3) The user computes F(sk; s), and uses σ to generate the key K from KeyGen(1k). He then calls DataRec(K; h) to get g = Qh- e and recovers the image x = Vf, where f is derived from g. |
| The extension to non-sparse data So far, we have been assuming that OIRS operates over sparse data only. That is, f is exactly sparse. However, there are many cases where physical data sources are not exactly sparse. To further broaden the application spectrum of OIRS design, we now show how to extend from the case of sparse data to the non-sparse general data. Specifically, assuming under orthonormal basis V, the image data x's coefficient vector f is non-sparse. We denote fs as an s-sparse approximation of f, which can be derived by setting all but the largest s entries of fto zero. Let xs= Vfs. Because V is orthonormal, then |
| ║x - xs║2 = ║Vf- Vfs║2 = ║f - fs║2. |
| And its difference compared to the actual s-sparse approximation fs satisfies the following bound, |
| ║ f* - f ║ ≤ Co/√2. ║ f - fs ║1, |
| Where C0 is some constant. |
| The above elaboration suggests that the aforementioned OIRS design can be still applied to the non-sparse general data. |
THEORETICAL ANALYSIS |
| Efficiency analysis |
| The most time-consuming operations in the proposed transformation is the matrix-matrix operations, which cost asymptotically O(n∝)for some 2 <∝< 3 due to m < 2n. On the other hand, solving the LP problem ΩK usually requires more than O(n3) time, e.g. [23]. Clearly, outsourcing image recovery service to cloud provides data owners/users considerable computational savings in theory. Moreover, with our proposed transformation, the cloud process can utilize any existing solvers for the LP problem ΩK , which ensures the cloud side efficiency This study in [13] has shown that using compressive sensing can reduce storage overhead up to 50%, compared to storing the original data or images in uncompressed format. |
FURTHER DISCUSSIONS |
| Enabling secure image outsourcing services will significantly boost the wide application spectrum of secure computing outsourcing. For example, the proposed OIRS can be adopted by image service applications like MRI in health care system, remote sensing in geographical system, and even military image sensing in various mission critical contexts. In the following, we give some further discussions on how the proposed OIRS can serve as a stepping stone and discuss the possible performance speedup through hardware built-in design. |
| A. Speedup with hardware built-in design |
| In order to make these promising image services in OIRS truly efficient and practically deployable, it is pivotal to further explore how to embed the security and efficiency guarantee from the start through a hardware design can significantly boost the performance of functionalities that are to be implemented in the proposed service architecture.For example, by giving the hardware design transformed image samples P(y + Ae) and the sensing matrix PAQ satisfying (PAQ) . (Q-1(f + e)) = P(f + Ae).Itwould still give us a randomly transformed output Q-1(f + e) as the encrypted result. |
EMPIRICAL EVALUATIONS |
| A. EXPERIMENT SETTINGS |
| We now show the experiment results of the proposed correlated compressed sensing with OIRS. We implement both the data owner/user and the cloud side processes in MATLAB and use the MOSEK optimization toolbox (http://www.mosek.com/) as the LP solver. All experiments are done on the same workstation with an Intel Core i5 CPU running at 2.90 GHz and 6 GB RAM. |
| B. EFFICIENCY EVALUATION |
| We first measure the efficiency of the proposed OIRS. Specifically we focus on the computational cost of privacy assurance done by the data owner and data users, i.e., the local side, and the cost done by the cloud side. The cloud solves it for the data user, who then performs a decryption process to get the original image data vector andthen recover the image. For completeness, we report the time cost here. For 32x32 image block it is 0.009 sec on average, while for 48_48 image block size it is 0.021 sec on average. |
| C. EFFECTIVENESS EVALUATION |
| We next assess the effectiveness of OIRS design. Our goal is to show the correctness of the design and also the empirical results on the privacy assurance. |
| 1. CORRECTNESS EVALUATION |
| For correctness of the design, we show that all the images, after transformation and later recovered on the data user side, still preserves the same level of visual quality as the original images. Here we want to point out that the reconstructed image quality increases along with the number of measurements and the more the better. In our experiments, we follow the ``four-to-one'' rule according to [11]. |
| 2.PRIVACY-ASSURANCE EVALUATION |
| Recall that OIRS provides the privacy-assurance that users can harness the cloud to securely recover the image without revealing the underlying image content. This can be achieved because what cloud really recovers, h, protects the original sparse vector h via a general afine mapping g = Qh- e with a random choices of Q and e. To give the empirical results on privacy-assurance,) the recovered image before user decryption, i.e., recovering using the blinded vector h = Q -1(g + e). |
CONCLUSION |
| In this paper we have proposed correlated Compressed Sensing, for image reconstruction. In this we apply correlated Compressed Sensing to image representation and propose a new image representation scheme. Different from the previous works on compressive imaging, which treat the whole image as a compressible signal, we decompose an image into two components: a dense component and a sparse component. The decomposition helps to generate a sparser signal which is proved more suitable for Compressed Sensing. The proposed method takes advantage of the correlation between dense and sparse components of the signal in the recovery procedure at the image decoder side.we also demonstrate a proof-of-concept of possible performance speedup through hardware built-in system design, which we believe is our important future work to be pursued. |
References |
|