Impact of Harvesting in Three Species Food Web Model With Two Distinct Functional Responses

Abstract

The intuition with two-species models may be applied to community food web questions. The critical behavior to community function may arise only through the interaction of three or more species. In this paper we investigate the dynamical behavior of the system consisting of two preys with distinct functional responses and a predator. We also study the effect of harvesting on prey species. Harvesting is strong impact on the dynamics evaluation of population. To a certain extent it can control the long term stationary density of population efficiently. Finally the local and global stability analyses were carried out.

Keywords

Food web, Functional response, Harvesting, Local and Global stability

INTRODUCTION

Population Dynamics has been a prime branch of theoretical ecology. Lotka- Volterra model describes interaction between two species in an ecosystem, a predator and a prey. The model was developed independently by Lotka [9] and Volterra [14]. After that more realistic prey-predator models were introduced by Holling [7] suggesting three kinds of functional responses for different species to model the phenomena of predation. Lotka- Volterra prey-predator model is one of the fundamental population models describing the species competency interaction in a closed habitual. The food web models are more complex and intractable as compared to food chains as more complex multilevel interactions are possible in food webs. Relatively less attention has been given to the study of food webs and their rich complex dynamical behavior [1],[4],[5],[11]. The authors [6] examined the steady state condition stability analysis and other comparivitive studies of two logistic models such as exponential and quadratic in the population dynamics of host-parasite interaction they have been observed that in the presence of parasite affects the logistic growth dynamics in the host. In Ecology there are huge number of food chain models with three or more species with different functional responses such as Holling-Tanner type[12,13], Beddington- Deangelis type[10,15] and ratio dependent type[2,3]. But most of the models have same type of growth rate and same functional response. From biological point of view, it is unrealistic in nature. In fact in the real world, predators feed on different types of consumption ways. Hence in this paper we consider two types of functional responses, one the Holling type-II and other Bedding ton- De Angelis functional response.

II. MATHEMATICAL MODEL

Consider a food web, comprising of two preys and one predator species. One of the prey species is harvested. The two prey species growing logistically and direct competition is considered between them. But they are apparent competition through the shared predation. Indeed, this apparent competition appears, as both prey types are included in predator’s diet. The mathematical model for the food web is given by the following system of equations,

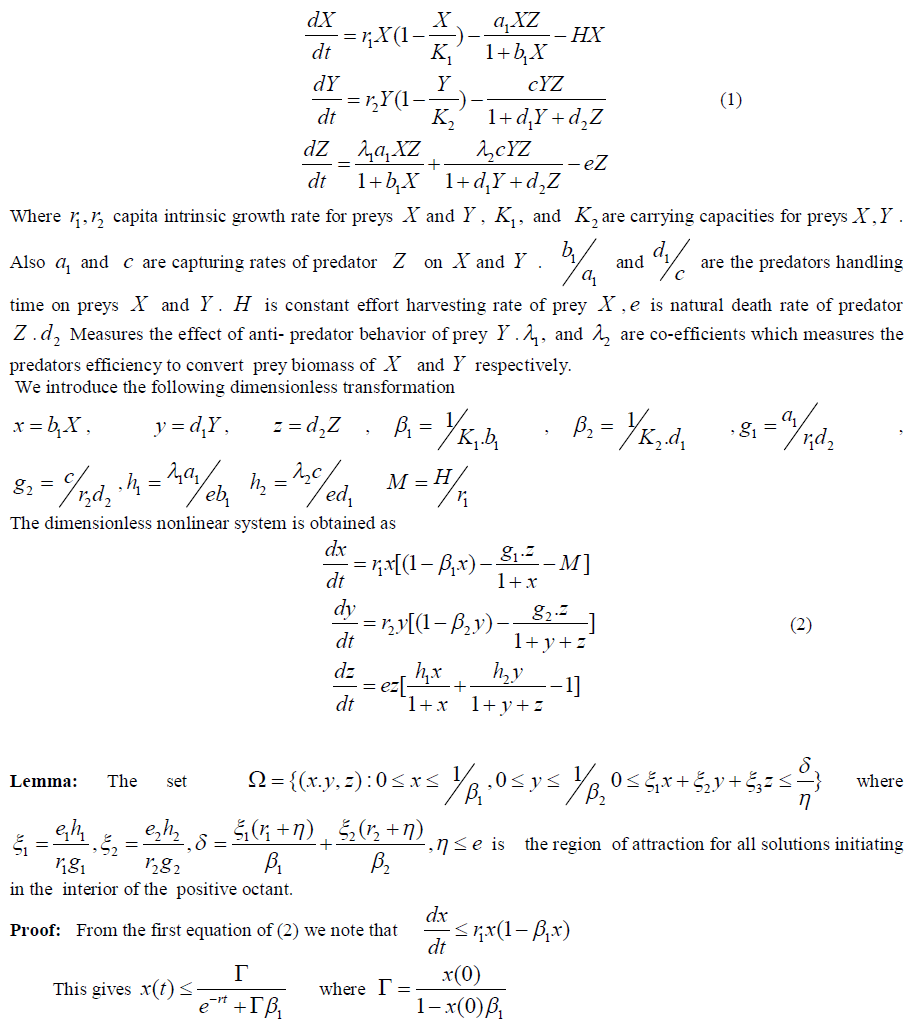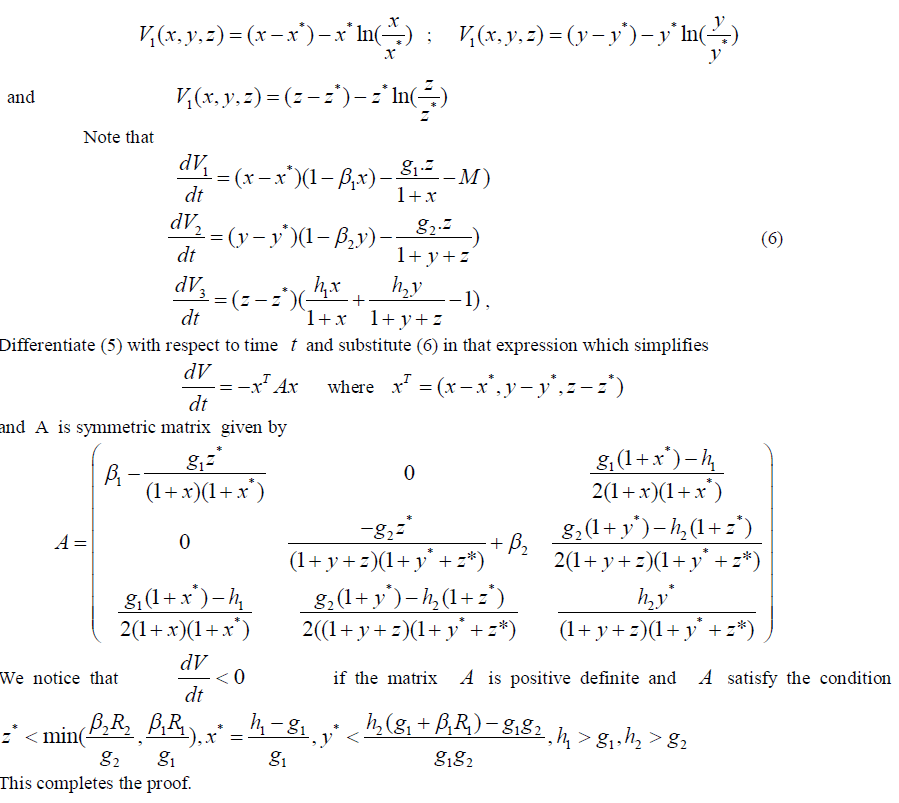IV. CONCLUSION

The use of harvesting efforts as to control to obtain strategies for the control of prey-predator system with non- monotonic functional responses and it shows a method how to control a prey- predator system and drive the state either to equilibrium points or to a limit cycle [8]. In paper we analyzed the dynamical behavior of three species food web with two distinct functional responses of Beddington- Deangelis and Holling type-II functional responses. We also obtain the condition for existence of different equilibrium and discussed their stabilities in local and global manners by using stability theory of differential equations. Finally we investigated the dynamical behavior of the system consisting of two preys with different functional responses and a predator. We also studied the effect of harvesting on prey species. We concluded that harvesting is strong impact on the dynamics evaluation of population. To a certain extent it can control the long term stationary density of population efficiently. The local and global analyses were carried out at the end.

References

1. Abd-Elalim A., Elsadany, 2012, “Dynamical complexities in a discrete-time food chain”, Computational Ecology and Software, 2(2):124-139.
2. B. Patra, A. Maiti, G. P. Samanta,2009, “Effect of Time-Delay on a Ratio-Dependent Food Chain Model”, Nonlinear Analysis: Modeling and Control 14, 199-216.
3. Dongmei Xiao, Wenxia Li, Maoan Han, 2006 “Dynamics in a ratio-dependent predator prey model with predator harvesting”, J. Math. Anal. Appl. 324, 14-29.
4. Gakkar s,Naji R .K, 2003, “Existence of chaos in two prey and one predator system. Chaos,Solitons&Fractals ,17(4):639-649
5. Gakkar s,Naji R .K,2002,“chaos in three species ratio dependent food chain. Chaos, Solitons&Fractals ,14:771-778
6. Gunasekaran. M., Veerakumari. L., 2008, “Bimodelling analysis of the population dynamics in the host parasite system”, IJACM, Volume no. 1, pp: (61-71).
7. Holling C.S. 1965, “The functional response of predator to prey density and its role in mimicry and population regulation”. Memoirs of the Entomological Society of Canada, 45: 1-60.
8. Kar T.K, chattopadhya .S, 2010,” dynamics of an exploited prey-predator system with non-monotonic functional response” Communications in Applied Analysis 14, 21–38.
9. Lotka A.J., 1925, Elements of mathematical biology, Williams and Wilkins, Baltimore, USA.
10. M. Fan, Y. Kuang,2004, “Dynamics of a non-autonomous predator-prey system with Beddington-DeAngelis functional response”, Journal of Mathematical Analysis and applications 295, 15-39.
11. Manju Agarwal., Rachana pathak.,2013, “Harvesting, Hopf Bifurcaion and chaos in three species food chain model with Beddington- De angelis type functional response”, JGRMA volume 1(1): 49-62.
12. S. Gakkhar, A. singh. 2012, “Control of Chaos due to additional predator in the Hasting-Powell food chain model”, J Math. Anal. Appl. 385.pp. 423-438.
13. T.K. Kar, H. Matsuda., 2007, “Global dynamics and controllability of a harvested prey-predator system with Holling type III functional response”, Non-linear Anal: Hybrid system 1, 59-67.
14. Voltera V. 1962. Opere matematiche: mmemorie e note, Vol V. Roma (Cremon): Acc. Naz. dei Lincei, Italy.
15. Y. Do, H. Baek, Y. Lim , D. Lim., 2011, “A three species food chain system with two types of functional responses”, Abstract and Applied Analysis, Vol No.10.