International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Implementation of Hardware for Source Identification using Pixel Non Uniformity Noise

T.Sathya1, Ms.R.Raja kumari2, R.Vinoth3
  1. PG scholar (M.E., VLSI design)
  2. Assistant professor/ ECE
  3. PSNACollege of Engineering and Technology, Dindigul, Muthayammal College of Engineering, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Digital camera identification can be accomplished based on sensor pattern noise which is unique to a device and serves as a distinct identification fingerprint. Camera identification and authentication has formed the basis of image / video forensics in legal proceedings. Unfortunately, realtime video source identification is a computationally heavy task, and does not scale well to conventional software implementations on typical embedded devices. In this paper, we propose a hardware architecture for source identification in networked cameras. The underlying algorithms, an orthogonal forward and inverse Discrete Wavelet Transform (DWT) and Minimum Mean Square Error (MMSE) based Estimation have been optimized for 2D frame sequences in terms of area and throughput performance. We exploit parallelism, pipelining and hardware reuse techniques to minimize hardware resource utilization and increase the achievable throughput of the design.

INTRODUCTION
DIGITAL camera identification has multiple applications in real-world scenarios. For example, when presenting a video clip as evidence in a court of law, identifying the source (acquisition device) of the video is as important as the video itself [1]. Not doing so can lead to legal challenges which may render the evidence invalid. Another example is the movie industry, where significant revenue losses are caused every year by secretive recording in movie theaters and the subsequent illegal distribution. Video source identification can be employed to track down such piracy crimes [2], [3]. Similarly, images or videos shared using Flickr, Facebook or other social networking sites or through personal email can be authenticated and tied to the user device (in this case, the smartphone or personal camera). Easier access to high-quality digital camcorders and sophisticated video editing tools further motivates the improvement of video source identification techniques. The issue of digital image or video authentication can be approached in several different manners. The simplest strategy would be to inspect the digital file itself and look for header clues or any other attached information. The EXIF header format [4], supported by many camera manufacturers contains information about the digital camera type and geo-location. However, this header data is unavailable if the video is transcoded or recompressed. Moreover, such tags can trivially be modified by software. Another strategy is to equip digital cameras with an invisible, yet fragile watermark carrying information about camera, location, time and personal biometric data. Such approaches are used in some highend cameras by Epson, Kodak and Canon [5], [6]. However, not every camera is equipped with such sensors.
The existing deployments such as surveillance camera networks or commercial image sharing in Smartphone’s are not equipped with such ‘securecameras’. The most reliable method reported so far for video source identification is based on the sensor pattern noise which is unique to each camera. This noise results from the nonuniformity of each sensor pixel’s sensitivity to light, and can be treated as the inherent fingerprint of a video capture device [7]. The scheme presented in [7] involves image denoising using the Discrete Wavelet Transform (DWT) followed by sub band level denoising using MMSE estimation procedure. In our experiments, we found computational requirements leading to large processing time (in the order of seconds per frame on multicore desktops for small resolution videos). The ‘db8’ DWT filter used in [7] has high computational requirements owing to the presence of irrational coefficients and a large number of taps. The MMSE estimation task uses 2D processing and is the most computationally expensive task (taking 99% of the entire processing time). Processing a single video frame (640 × 480 resolution) on an Intel core i7 laptop takes about 5 seconds, giving an effective throughput of only 184 KBps. The expensive computation overhead will become a bottleneck when fast identification is needed. An example is detecting video camera spoofing attacks using source identification techniques.
An adversary can compromise a legitimate camera, and then send fake video to the sink using the victim’s identity. Such an attack is called camera spoofing attack, which introduces severe security threats if the camera is used for surveillance or other security purpose. Moreover, given the increasing popularity of wireless video cameras, such attacks are becoming easier to launch. The sensor pattern noise based source identification method is naturally a good candidate to detect this attack; however, it requires performing source identification in a realtime fashion.

LITERATURE REVIEW
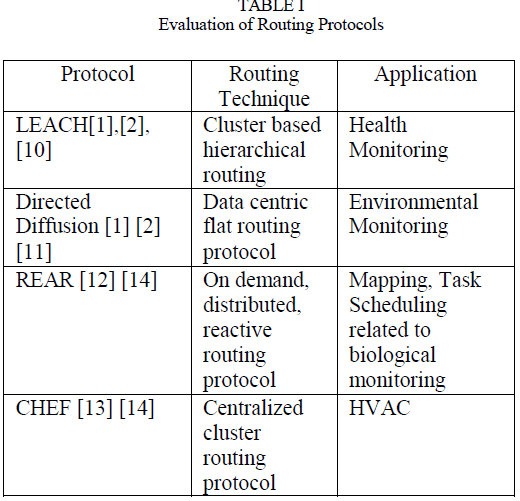
The research on image source identification emerged a few years prior to video source identification, and the techniques are often similar. Kharrazi et al. [8] proposed a novel idea for camera identification based on supervised learning. They compute image features in spatial and wavelet domain and then train a Support- Vector-Classifier to find camera model. A multiclass SVM classifier is used to identify and classify images from 5 different cameras with an accuracy of 78 − 85%. Similarly, Celiktutan et al. [9] defined a set of similarity measures using KNN and SVM for classification operation. Choi et al. [10] include intrinsic lens radial distortions as part of the features and improve classification. Popescu [11] uses the Expectation Maximization algorithm to identify the demosaicing algorithm that a camera uses, based on which different image sources are classified. However, all these methods are only capable of detecting the model or the manufacturer of the device, instead of identifying the individual camera that produced the image. The following techniques focus on the specific device identification, which is desirable for the forensic applications. The Canon Data Verification Kit [6] calculates the hash of images and uses a special secure memory card to enable tracing the image to a camera, but only high-end Canon DSLR cameras support this solution. The same applies to embedding watermarks into images, which is only applicable for specially designed devices rather than commodity devices. Geradts et al. [12] proposed to utilize sensor hot pixels or dead pixels to identify the image source. It performs nicely even for JPEG compressed images. However, all cameras do not have such defective pixels, and many cameras post-process to remove such defects from output images.
Kurosawa et al. [13] measured the dark current noise of the sensor and used it as the device fingerprint. Since the dark current noise can only be extracted from dark frames, this method is restricted to the videos that contain dark frames. Lukas et al. [7] employed sensor pattern noise as an inherent fingerprint of the camera for source identification. More specifically, they use Photo- Response Non-Linearity (PRNU) noise to identify the individual video camera. So far, the sensor pattern noise based schemes report the most reliable results. Kang et al. [14] model this noise as a white noise signal to improve the detection statistics in cases of images suffering from interference and losses by JPEG compression and the camera signal processing. Li [15] proposed to use adaptive weighting to improve the performance of this approach. Recent work by Li et al. [16] consider the interference caused by interpolation process in color filter arrays in PRNU extraction and propose a color-decoupled PRNU extraction process. Chen et al. [3] extend this prior work to networked videos. However, they require as long as 10 minutes of processing time for low resolution (264 × 352) and 40 seconds for higher resolution (536 × 720) videos. The work of [17] improves this value to 10 seconds ( 300 − 400 frames) using network characteristics.

PROPOSED SYSTEM
image
3.1.Pre-processing
We introduce a pre-processing block to reduce redundant computations in our PE array and introduce hardware reuse. The squaring operation (of subband coefficient done for each computation) is redundant. Hence, instead of squaring for each operation, we input squared values of the pixels themselves and normalize them with the input variance value.
Much research has been done in the development of DWT architectures for image processing . A good survey on architectures for DWT coding is given by [20], however the focus has been primarily on image compression applications. The DWT architectures can be broadly classified into lifting based, convolutionbased and B-spline based architectures. The lifting based architectures are popular and became the mainstream because they need fewer multipliers and adders and have a regular structure. Similarly B-spline-based architectures have been proposed to minimize the number of multipliers by using B-spline factorization [22]. However, the lifting based architecture has a larger critical path. Convolution-based approaches have a lower critical path but require a larger number of multipliers. These filters designed for image compression and efficient implementation degrades quickly for image denoising applications. The 9/7 poly-DWT filter in [21] has best known image compression and hardwareefficient implementation. Figure 3 shows this effect where denoising causes distortions when using 9/7 filter. This is because denoising applications typically use orthogonal wavelets while compression codecs use CDF 9/7 and similar filters which are based on bi-orthogonal wavelet construction.
image
Modified Filter Bank implementation
The authors propose using ‘db8’ orthogonal wavelet for denoising operation. Named after Ingrid Daubechies who did monumental research on wavelets and their applications, ‘db8’ is an orthogonal and asymmetric wavelet filter. The filter coefficients are irrational and asymmetric and 16 taps are present in both decomposition of low pass LoD and high pass HiD filters. They are all distinct and irrational (truncated values are shown). Consequently, a direct implementation in hardware will require 16 multipliers and subsequent 15 adders to get a high or low pass output. The filter is asymmetric and no coefficients are same across high and low pass filter. Use of 32 multipliers and 30 adders to obtain a single level of wavelet decomposition will lead to significant area and computational requirements.
PE array
The PEs are arranged in a 2D systolic array. We note some interesting properties which help us to optimize the implementation of the MLE block: 1) Pipelining: Since the computations between subsequent pixels reuse most of the pixels (except one row / column which needs to be input), we use a pipeline which inputs along the short edge (row/ column). Thus, effectively only three pixels are input every clock cycle. We refer to this as our Naive implementation. 2) Parallelism: The larger windows overlap over smaller windows, making it possible to do the computations concurrently. This step leads to 5X speedup because the number of computations required are greatly reduced and can be reused amongst the masks.
3.3.Post-processing
The denoised subband pixel is obtained above using the MMSE value from the PE array and the subband value. Then, the PNU estimate is obtained as P1
P1(i, j) = I(i, j) − Ī(i, j)
where image Ī is obtained after inverse DWT operation on the denoised subbands. Next we compute the correlation between pixels in pnu p and p1.Based on the comparision of correlated value with the threshold the source is considered matched.

SIMULATION RESULTS
image
image
image
image

CONCLUSIONS
In this paper, we proposed architectures for hardware acceleration of video authentication algorithm using pixel-nonlinearity noise to identify the original camera. Our algorithm is able to accurately authenticate source camera using 650 frames from source video. We proposed a modified filter bank approach for DWT and IDWT implementation which reduces the hardware requirements and achieves a clock frequency of 167 MHz. We also presented a 2D systolic array architecture for wavelet subband denoising which was optimized for hardware requirements and performance using rectangular masks and suitable design.

References
  1. O. Kerr, “Searches and seizures in a digital world,” Harvard Law Review, vol. 119, p. 531, 2005.
  2. F. Lef`ebvre, B. Chupeau, A. Massoudi, and E. Diehl, “Image and video fingerprinting: forensic applications,” Media Forensics and Security, pp. 725 405–725 405–9, 2009.
  3. M. Chen, J. Fridrich, M. Goljan, and J. Lukas, “Source digital camcorder identification using sensor photo response nonuniformity,” in Proceedings of the SPIE, vol. 6505, 2007.
  4. K. Cohen, “Digital still camera forensics,” Small Scale Digital Device Forensics Journal, vol. 1, no. 1, pp. 1–8, 2007.
  5. P. Blythe and J. Fridrich, “Secure digital camera,” in Digital Forensic Research Workshop, 2004, pp. 11–13.
  6. “Canon data verification system,” online, http://cpn.canoneurope.com/content/education/infobank/image verification/canon data verification system.do, 2013.
  7. J. Lukas, J. Fridrich, and M. Goljan, “Digital camera identification from sensor pattern noise,” IEEE Transactions on Information Forensics and Security, vol. 1, no. 2, pp. 205–214, 2006.
  8. K. Mehdi, H. Sencar, and N. Memon, “Blind source camera identification,” in International Conference on Image Processing, vol. 1. IEEE, 2004, pp. 709–712.
  9. O. C¸ eliktutan, B. Sankur, and I. Avcibas, “Blind identification of source cell-phone model,” IEEE Transactions on Information Forensics and Security, vol. 3, no. 3, pp. 553–566, 2008.
  10. K. Choi, E. Lam, and K. Wong, “Automatic source camera identification using the intrinsic lens radial distortion,” Optics Express, vol. 14, no. 24, pp. 11 551–11 565, 2006.
  11. A. Popescu and H. Farid, “Statistical tools for digital forensics,” in Information Hiding. Springer, 2005, pp. 395–407.
  12. Z. Geradts, J. Bijhold, M. Kieft, K. Kurosawa, K. Kuroki, and N. Saitoh, “Methods for identification of images acquired with digital cameras,” Enabling technologies for law enforcement and security, vol. 4232, no. 1, pp. 505–512, 2001.
  13. K. Kurosawa, K. Kuroki, and N. Saitoh, “CCD fingerprint methodidentification of a video camera from videotaped images,” in Proceedings International Conference on Image Processing, vol. 3. IEEE, 1999, pp. 537–540.
  14. X. Kang, Y. Li, Z. Qu, and J. Huang, “Enhancing source camera identification performance with a camera reference phase sensor pattern noise,” IEEE Transactions on Information Forensics and Security,, vol. 7, no. 2, pp. 393–402, 2012.
  15. C. Li, “Source camera identification using enhanced sensor pattern noise,” IEEE Transactions on Information Forensics and Security, vol. 5, no. 2, pp. 280–287, 2010.
  16. C.-T. Li and Y. Li, “Color-decoupled photo response nonuniformity for digital image forensics,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 22, no. 2, pp. 260–271, 2012.
  17. S. Chen, A. Pande, K. Zeng, and P. Mohapatra, “Video source identification in lossy wireless networks,” in IEEE International Conference on Computer Communications, (Infocom) miniconference. IEEE, 2013.
  18. W. Van Houten and Z. Geradts, “Source video camera identification for multiply compressed videos originating from youtube,” Digital Investiga- tion, vol. 6, no. 1, pp. 48–60, 2009.
  19. D. Hyun, C. Choi, and H. Lee, “Camcorder identification for heavily compressed low resolution videos,” Computer Science and Convergence, pp. 695–701, 2012.
  20. T. Acharya and C. Chakrabarti, “A survey on lifting-based discrete wavelet transform architectures,” The Journal of VLSI Signal Processing, vol. 42, no. 3, pp. 321–339, 2006.
  21. M. Martina and G. Masera, “Multiplierless, folded 9/7 - 5/3 wavelet VLSI architecture,” IEEE Trans. Circuits and Systems II, vol. 54, no. 9, pp. 770–774, Sep. 2007.
  22. C.-T. Huang, P.-C. Tseng, and L.-G. Chen, “VLSI architecture for discrete wavelet transform based on B-spline factorization,” Proc. IEEE Work.Signal Processing Systems, 2003. SIPS 2003, pp. 346–350, Aug. 2003.