ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
J.Bamela Mary1, K.Ramamoorthy2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
For efficient hardware implementation many designers designs several multiplier structure based on different techniques. But these designs are achieving only 30% of power reduction and 28% of area reduction. In this paper we propose a low complexity and low latency multiplier in order to reduce the requirement of power and area. The proposed work is fully based on the distributed arithmetic algorithm (DAA) which provides the better performance than the existing designs. The proposed design will be coded in verilogHDL and synthesized in Xilinx ISE9.2i. From the synthesized result we will prove the modified structure that requires less area and less power than the existing ones. Finally the proposed design will be implemented on FPGA spartan3E hardware.
Index Terms |
| All-one polynomial, finite field, systolic design. |
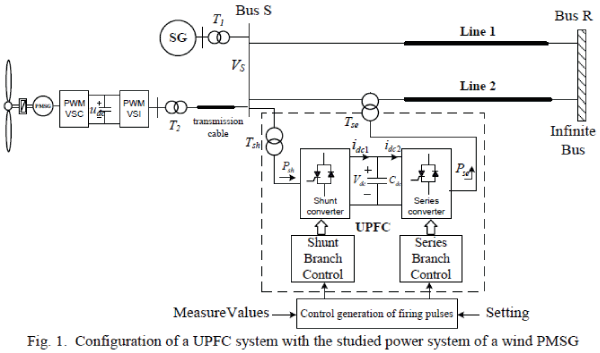
INTRODUCTION |
| Finite field multipliers over GF(2^m) have wide applications in elliptic curve cryptography (ECC) and error control coding systems . Polynomial basis multipliers are popularly used because they are relatively simple to design, and offer scalability for the fields of higher orders. Efficient hardware design for polynomial-based multiplication is therefore important for real-time application.All-one polynomial (AOP) is one of the classes of polynomials considered suitable to be used as irreducible polynomial for efficient implementation of finite field multiplication. Multipliers for the AOPbased binary fields are simple and regular, and therefore, a number of works have been explored on its efficient realization. Irreducible AOPs are not abundant. They are very often not preferred in cryptosystems for security reasons, and one has to make careful choice of the field order to use irreducible AOPs for cryptographic applications. The AOP-based multipliers can be used for the nearly AOP (NAOP) which could be used for efficient realization of ECC systems. AOP-based fields could also be used for efficient implementation of Reed- Solomon encoders.Besides, the AOP-based architectures can be used as a kernel circuit for field exponentiation, inversion, and division architectures. Systolic design is a preferred type of specialized hardware solution due to its high-level of pipeline ability, local connectivity and many other advantageous features. In a bit-parallel AOP-based systolic multiplier has been suggested by Lee et al. In a recent paper a low-complexity bit-parallel systolic Montgomery multiplier has been suggested. Very recently an efficient digit-serial systolic Montgomery multiplier for AOP-based binary extension field is presented. The systolic structures for field multiplication have two major issues. |
| First, the registers in the systolic structures usually consume large area and power. Second, the systolic structures usually have a latency of nearly n cycles, which is very often undesired for real-time applications. Therefore, in this paper, we have presented a novel register- sharing technique to reduce the register requirement in the systolic structure. The proposed algorithm not only facilitates sharing of registers by the neighboring PEs to reduce the register complexity but also helps reducing the latency. Cut-set retiming allows to introduce certain number of delays on all the edges in one direction of any cut-set of a signal flow-graph (SFG) by removing equal number of delays on all the edges in the reverse direction of the same cut-set . When all the edges are in a single direction, one can introduce any desired number of delays on all the edges of any cut-set of an SFG. Therefore, this technique is highly useful for pipelining digital circuits to reduce the critical path. In this paper, we have proposed a novel cut-set retiming approach to reduce the clock-period. The proposed structure is found to involve significantly less area-time-power complexity compared with the existing designs. |
RELATED WORK |
| In fact, real-time signals may also be processed in this manner if the associated blockprocessing delay is acceptable. Another potentially important application for backward filtering is the implementation of Mallat two-channel iterated filter banks based on power-complementary Butterworth filters (wavelets). The zero-phase case is often used to implement frequency-selective infinite-impulse response (IIR) filters corresponding to the squaredmagnitude of the classical Butterworth, Chebyshev, and elliptic designs. However, other interesting and potentially important applications exist for non causal IIR filters that are not zero-phase. Examples include equalizers for non minimum- phase systems, non causal speech models, half-sample interpolators, and 90-degree phase shifters such as Hilbert transformers and differentiators. On the other hand, many fast algorithms in the context of digital filtering have been obtained based on particular matrix structures. Many approaches to block digital filters (BDFs) design exist. Some approaches compel the BDF to be time-invariant so that conventional filter synthesis techniques can be used. The best known and most widely used approach is Overlap-save. In some other approaches, no such constraint on the BDF is imposed so that the BDF can be time variant. |
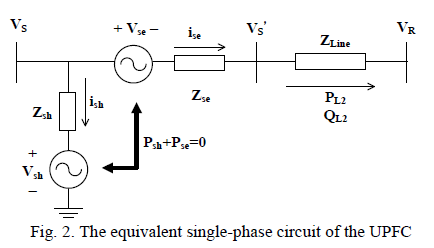
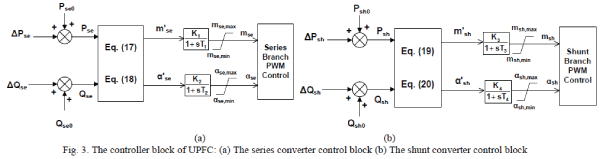
PROPOSED SYSTEM ARCHITECTURE |
| Let A,B and C are the extended polynomials and these are represented as: |
 |
 |
| Fig(3.1) General Signal Flow Graph |
 |
 |
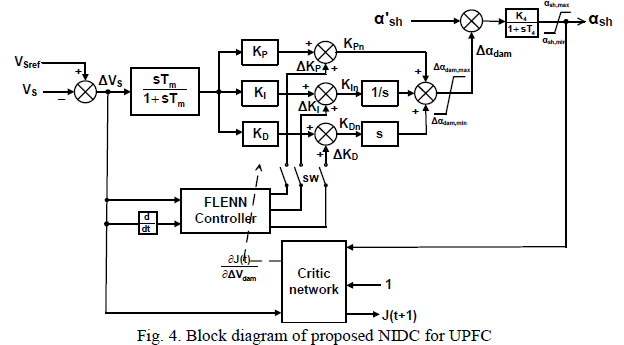
| Architecture for 1 *N convolution and 1-bit input: |
| Most 2-D convolution implementations rely on the multiplying units embedded in modern FPGAs to carry out all the multiplications in parallel and to achieve great performance. However, as the kernel size increases, the number of embedded multipliers needed grows exponentially. This fact can constrain the kernel size or force to use a bigger FPGA device, which, in its turn, can yield a very high cost per operation ratio. On the other hand, a lot of work has been done on the design of multiplier less filters, mostly in the one-dimensional domain, and some authors have implemented 2-D convolution by replacing multiplications with shifting and adding operations or transforming the computation into the logarithmic domain. |
 |
 |
 |
 |
CONCLUSION |
| Efficient systolic design for the multiplication over GF(2^m) based on irreducible AOP is obtained in my existing system. By using cut-set retiming technique the critical path is reduced to one XOR gate delay and by sharing of registers for the input-operands in the PEs, the low-latency bitparallel systolic multiplier have been derived. For self checking I have simulated in modelsim. For evaluating the performance parameter I have used Xilinx ISE 9.2i. In my existing system the total power consumption is 81mW, latency is 11.771ns and required number of gates are around 650. Moreover the existing design will be reconstructed for reduce the latency, power requirement and gate count by using distributed arithmetic algorithm. |
References |
|