International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Improved Estimation Performance of Sensor in Wireless Sensor Network Using Suboptimal Technique

S.Vinotha1, G.Yogarajan2, T.Revathi3
  1. PG Scholar, Department of Information Technology, Mepco Schlenk Engineering College, India.
  2. Senior Assistant Professor, Department of Information Technology, Mapco Schlenk Engineering College, India.
  3. Senior Professor and head, Department of Information Technology, Mepco Schlenk Engineering College, India.
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper presents a novel network lifetime extension technique. In order to collect information more efficiently, wireless sensor networks (WSNs) are partitioned into clusters. Clustering provides an effective way to prolong the lifetime of WSNs. Current clustering approaches often use two methods: selecting cluster heads with more residual energy, and rotating cluster head periodically, to distribute the energy consumption among nodes in each cluster and extend the network lifetime. However, most of the previous algorithms have not considered the expected residual energy, only consider the estimation performance. In this paper we propose a probabilistic based transmission using clustering algorithm. Probabilistic transmission control at which is to minimize the mean squared error of estimation by increasing the packet transmission success probability of only sensors having high observation SNR. These newly available sensors are partitioned into several sensor sets select the cluster head to maintain the same estimation performance. The simulation results show that the proposed approach is more efficient than other distributed algorithms. It is believed that the technique presented in this paper could be further applied to large-scale wireless sensor networks.

Index Terms
distributed estimation, wireless sensor network, clustering technology

INTRODUCTION
Wireless sensor nodes are highly energy constrained devices. They have limited battery life due to various constraints of sensor nodes such as size and cost, etc [1]. Clustering of sensor nodes is an effective method to use the node energy optimally and prolong the lifetime of energy constrained wireless sensor network. A shared communication system like ALOHA requires a method of handling collisions that occur when two or more systems attempt to transmit on the channel at the same time. In the ALOHA system, a node transmits whenever data is available to send. If another node transmits at the same time, a collision occurs, and the frames that were transmitted are lost. However, a node can listen to broadcasts on the medium, even its own, and determine whether the frames were transmitted.
Distributed estimation of wireless sensor network depends upon the large number of deployed sensors. Estimation performance equipped with a performance of fusion center and the communication radio transceiver. The cross layered slotted aloha protocol maximize the estimation performance but not the system throughput. However, these studies did not necessarily optimize the problem solutions since the focus was not on system throughputs but on the accuracy of the estimate obtained by the data collected from sensors at the FC in distributed estimation problems [2]. In [9], network lifetime analysis was conducted with a special focus on distributed estimation problems. This technique allocates transmission power and the number of quantized bits of observation to selected sensors to maximize network lifetime. However, since this technique cannot control the probability of packet transmission, packet collisions in multiple random access systems, such as slotted ALOHA systems, cannot be reduced, and thus, estimation performance may be degraded. Except for [9], most studies on WSNs have not explicitly addressed network lifetime techniques that consider the estimation accuracy in distributed estimation problems. This paper presents a novel network lifetime extension technique that uses probabilistic transmission control for distributed estimation in WSNs with a static or quasi-static environment. The presented technique increases the number of available sensors relative to conventional techniques. Sensors not selected in conventional techniques can be incorporated into the presented technique to obtain final estimates. As a result, the number of usable sensors in the networks increases. These newly available sensors are partitioned into several sensor sets to maintain estimation performance. Since observation and transmission for each sensor set are not carried out in every observation period, the network lifetime can be expected to be extended for a given estimation performance.
image

SYSTEM MODEL
Consider wireless sensor network with N number of sensors. In order to increase the estimation performance in wireless sensor network available sensors are divided into several sets. Select the cluster heads with more residual energy and rotating the cluster heads periodically.
Using low energy adaptive hierarchy protocol (LEACH) to select the cluster head. N numbers of sensors observe the unknown parameter θ. Distribute the residual energy among the nodes in each cluster each sensor observe unknown parameter θ. The ith observation yi,m in the mth observation period obtained during the observation total period T.
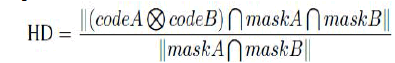image
image
where hi,m and ni,m are the observation channel coefficient and additive observation noise. The observations are corrupted by additive noise. Sensor i transmit in the tth time slot to the fusion center to perform local estimation. The ith sensor gain αi,m[t] is given by
image
we fix the average transmission power of each sensor satisfy the power constraint p given by
image
Normalized received message of fusion center is yi,m[t] at the tth time slot is defined as
image
Where hi,m is the channel coefficient from observed data to sensor and from sensor to the fusion center.
image
image
image

MAXIMUM MSE-REDUCTION (MMR) METHOD
In this section, we describe the proposed MMR method where the transmission probabilities, are derived to maximize the MSE reduction in each time slot [2]. The method relies on the knowledge of the accumulated SNR before the current transmission takes place image
image
image

NETWORK LIFETIME
We consider each sensor is battery powered. Lifetime wireless sensor network fully depend upon the sensors battery capacity. If anyone of the sensors battery power is drained at any situation when the lifetime of sensor network is risk. Initial residual for each sensor is Ɛ0 [15]. If anyone of the sensor consider as dead then the residual energy is dropped Ei≤Ɛ0. Ei is residual energy of sensor i. Conventional techniques select sensors with high observation of signal to noise ratio (SNR) for observation transmission and the remaining sensors are ignored, even if the batteries of the selected sensors are exhausted. Therefore to solve the problem, increase the ratio of available sensor to all sensors given by
image

CLUSTERING METHODOLOGY
Wireless sensor network use clustering mechanisms to achieve the energy efficiency in the communication efficiency between sensor nodes. The operation of LEACH [7], [8] is divided into several rounds. Each round begins with a set-up phase when the clusters are organized, followed by a steady-state phase when data are transferred from the nodes to the cluster head (CHs) and on to the base station. LEACH forms clusters by using a distributed algorithm, where nodes make autonomous decision without any centralized control.
image
Where G is the set of nodes that have not been CHs in the 1/p rounds. Each sensor node decide independently to other sensor nodes whether it will claim to be CH or not, by selecting randomly r between 0 and 1.
However, in some cases, inefficient CHs can be selected. Because LEACH depends on only a probabilistic model, some cluster heads may be very close each other and can be located in the edge of WSNs. These inefficient cluster heads could not maximize the energy efficiency. Appropriate cluster-head selection can significantly reduce energy consumption and prolong the lifetime of WSNs.
A. Clustering Algorithm
Probability P, Set of nodes n
Einit(i)=E0, i=1,2,..,n
image
image
B. Expected Residual Energy
Number of members is unknown before the cluster formation. Neighbors obtain expected energy during cluster head selection. CH has n cluster members [3] , it would receive n messages from all members and transmit one combined message to the fusion center with distance dfc. The number frames can be obtained by
image
Where tslot is the time required for transmission from members to cluster Head, tssp is the operation time of steady state phase and tCHtoFC is the time required for the transmission from CH to FC.
image
image
The expected residual energy of node to CH and expected consumed of node to CH in steady state phase

PROBABILISTIC TRANSMISSION CONTROL FUNCTION
Sensor nodes are usually scattered in a sensor fields. The scattered sensor has capability to collect data and route data to sink. We propose dynamic probabilistic transmission control scheme to reduce the redundant packet transmission. Each node probabilistically decides to transmit packet to neighbors. The transmission control function at the tth time slot of ith sensor SNR is given by
image
image (MMSE). We will take the cumulative distribution function of the threshold value of the MMSE that will give the average transmission probability of each sensor
image
Minimize the mean square error for taking average transmission probability of observed signal to noise ratio by using threshold value of the average MMSE of total observation period T.
image
Successive packet transmission of sensor is based on the expired sensors and active sensors at the tth time slot. The active sensors at the tth time slot lesser than the (t-1)th time slot. Because, each and every round the energy for each sensor is reduced based on their observation and transmission of data.
image
Where Nα is the number of sensor SNR above the threshold and Nexp expired sensors at the tth time slot.
In one observation period of sensors successive transmission probability denoted by
image

SUBOPTIMAL SOLUTION
image
image
The observation SNR δi can be modeled as an exponential random variable return as
image
Where  is the average value of observation SNR. There are number of cluster sets are formed with the help of leach protocol. Successive packet transmission for one observation period can be written as
image
image
image
Threshold value signal to noise ratio (SNR) of
image
Finally, based on the results given in this section, we develop an algorithm to obtain suboptimal threshold value of SNR Δk.
image

NUMERICAL RESULT
In this section, we provide numerical results to validate the effectiveness of the presented technique. These results have to improve the estimation performance of sensor in each cluster than the existing conventional technique. The technique is expected to be applicable to distributed estimation. To evaluate the presented technique lifetime extension capability is represented as Lp .
All the results presented in this section are obtained by averaging over 10 000 independent trials. In this section, we set μθ to 20 dB, θ ~ N(0, σ2θ ), and σ2θ = 1. Moreover, we set the observation period T to T = αN, where α is a positive value, and 0 < α < 1. The presented technique can use sensors more effectively than the conventional technique .One can also see that the performance of the ASSR does not depend on the length of the observation period. The number of spare sensors increases by using the presented technique.
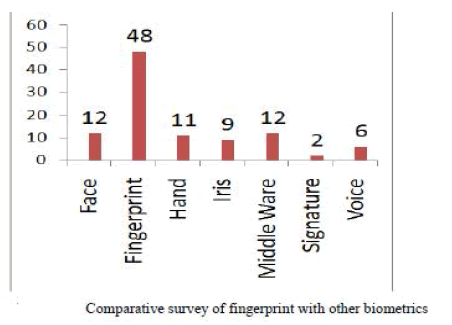
image
Fig.3. represents the lifetime extension capability versus number of sensors. The lifetime extension of sensor network varied each observation period based on the total observation time and the parameter α0(0-1). The above figure represent lifetime extension of sensor given α values are 0.125, 0.25, 0.375 and 0.5.
Network lifetime extension capability technique is to increase the lifetime of wireless sensor network. Network lifetime defined as duration of time that the estimation performance is obtained. In every observation period, the number of sensor in each sensor set is increased by means of which the network lifetime is increased.
We will increase the available sensor ratio in every observation period of the cluster sets. Based on the various values of the parameter α0 (fig.3) the lifetime of sensor network is analyzed and observed to be increased.
image
Fig .4 Mean Square Error performance of different number of sensor T=αN
Mean squared error for different number of sensor is obtained to estimate overall measure of the minimized mean square error in network. Mean squared error of an estimator quantify difference between the values and measures the squares of the errors. The fusion center estimates the overall observation of every cluster sources.
It will require minimizing the mean squared error of the sensors using the observation parameter α0. The total observation of SNR is increased relatively so that the MSE of the overall sensors will be minimized.
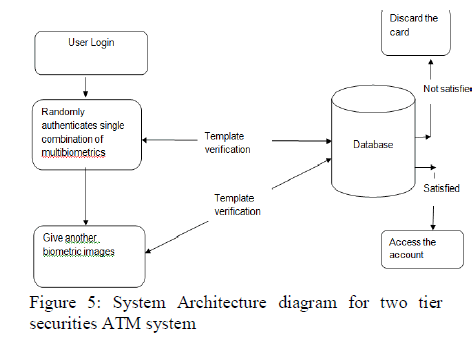
image
Fig.5 Performance of available sensor to all sensor ratio for different number of sensor T=Αn
Lifetime of sensor network fully depend upon the available sensor battery capacity. In previous techniques it does not efficiently increase the lifetime of sensor network because limited number of sensors only involved during the transmission and observation. We have to increase the lifetime of overall network to increase the available sensor ratio in each observation period. In fig.5 represents the available sensor to all sensor ratio based on the parameter α0.
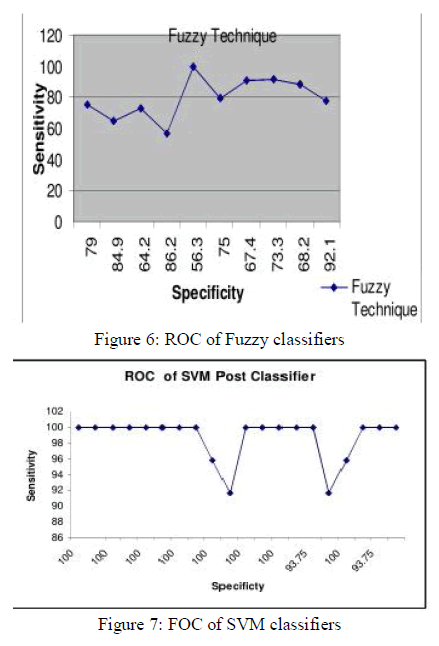
image
Fig.6. Performance of normalized standard deviation of MSE for different number of sensor T=αN
In Fig.6. Minimize the redundancy of network performance in which to perform a normalized standard deviation of number of sensor observation. Using various values of parameter α0 to vary the observation period of sensor to measure how the normalized standard deviation is varied among the number of clusters. Normalized standard deviation is just the standard deviation divided by the mean. We will take a normalized standard deviation for the mean square error with the help of generated mean. Finally the normalized value of mean square error is attained and it will give a reduced value of mean square error for number of divided sensor set.

CONCLUSION AND FUTURE WORK
This paper presents a network lifetime extension technique using probabilistic transmission control technique with clustering. In this technique increase the number of sensor with increased battery capacity. Obtain minimization of mean square error using clustering of sensor nodes. Numerical results were shown to shown to provide the effectiveness of the estimation. We introduce sensor node selection algorithm with power constrained. To extend the network lifetime by means of using an improved clustering mechanism in order to maximize lifetime of sensor network with constrained energy. Designing scenarios which depict real world applications more accurately can be designed through indepth study of the applications

References
  1. Akyildiz, W. Su, and E. Cayirci, “Wireless sensor networks: A survey,”Comput. Netw., vol. 38, no. 4, pp. 393–422, Mar. 2002.
  2. Y.-W. P. Hong, K.-U. Lei, and C.-Y. Chi, “Channel-aware random access control for distributed estimation in sensor networks,” IEEE Trans. Signal Process., vol. 56, no. 7, pp. 2967–2980, Jul. 2008.
  3. J.S.Lee “Fuzzy-Logic-Based Clustering Approach for Wireless Sensor Networks Using Energy Predication,” IEEE SENSORS JOURNAL, VOL. 12, NO. 9, SEPTEMBER 2012
  4. Imad S. AlShawi, Lianshan Yan, “Lifetime enhancement in wireless sensor network using fuzzy approach and A-star algorithm”IEEE Sensor Jornal VOL. 12, NO. 10, OCTOBER 2012
  5. Y. Chen and Q. Zhao, “An integrated approach to energyaware medium access for wireless sensor networks,” IEEE Trans. Signal Process., vol. 55, no. 7, pp. 3429–3444, Jul. 2007.
  6. S.Narieda“Lifetime extension of wireless sensor network using probabilistic transmission control for distributed estimation in wireless sensor network” IEEE Trans.vechicular Technology VOL. 61, NO. 4, MAY 2012
  7. S. Narieda, “Probabilistic transmission control for distributed estimation in wireless sensor networks,” in Proc. IEEE Top. Conf. WiSNet, 2011, pp. 73–76.
  8. W. R. Heinzelman, A. Chandrakasan, and H. Balakrishnan, “Energyefficient communication protocol for wireless microsensor networks,”in Proc. IEEE Annu. Hawaii Int. Conf. Syst. Sci., Jan. 2000, pp. 3005–3014.
  9. W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “An application-specific protocol architecture for wireless microsensor networks,”IEEE Trans. Wireless Commun., vol. 1, no. 4, pp. 660– 70,Oct. 2002.
  10. J. Li and G. AlRegib, “Network lifetime maximization for estimation in multihop wireless sensor networks,” IEEE Trans. Signal Process., vol. 57, no. 7, pp. 2456–2466, Jul. 2009.
  11. T.-Y. Chang, T.-C. Hsu, and Y.-W. P. Hong, “Exploiting data-dependent transmission control and MAC timing information for distributed detection in sensor networks,” IEEE Trans. Signal Process., vol. 58, no. 3, pp. 1369–1382, Mar. 2010.
  12. A. Ribeiro and G. Giannakis, “Bandwidth-constrained distributed estimation for wireless sensor networks, Part i: Gaussian case,” IEEE Trans. Signal Process., vol. 54, no. 3, pp. 1131–1143, Mar. 2006.
  13. Ribeiro and G. Giannakis, “Bandwidth-constrained distributed estimation for wireless sensor networks, Part II: Unknown pdf,” IEEE Trans. Signal Process., vol. 54, no. 7, pp. 2784–2796, Jul. 2006.
  14. J.-J. Xiao, A. Ribeiro, Z.-Q. Luo, and G. Giannakis, “Distributed compression-estimation using wireless sensor networks,” IEEE Signal Process. Mag., vol. 23, no. 4, pp. 27–41, Jul. 2006.
  15. J.-J. Xiao, S. Cui, Z.-Q. Luo, and A. J. Goldsmith, “Power scheduling of universal decentralized estimation in sensor networks,” IEEE Trans. Signal Process., vol. 54, no. 2, pp. 413–422, Feb. 2006
  16. Y. Chen and Q. Zhao, “An integrated approach to energyaware medium access for wireless sensor networks,” IEEE Trans. Signal Process, vol. 55, no. 7, pp. 3429–3444, Jul. 2007.

APPENDIX
image