ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Nishok.V.S, Shaheema.S, Dr.P.Poongodi Department of Electronics and Communication Engineering, PPG Institute of Technology, Coimbatore-35, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Multipliers play a key role in the high performance digital systems. Design considerations of multipliers include the following- high speed, low power consumption, regularity of layout and hence less area or even combination of them, making them suitable for various compact high speed, low power VLSI implementations. However area and speed are two conflicting constraints and improving speed results always in larger areas. A booth multiplier is a parallel multiplier that uses carry look ahead algorithm. A new (4:2) compressor design for Booth multiplier is proposed in order to reduce latency and improve speed. The key design point is to use an available signal, in the sum path, for carry generation. The comparison of these Architectures is carried out to know the best architecture for multiplication with respect to power and delay characteristics. The designs are implemented using Tanner and synthesis is done.
INTRODUCTION |
| Multipliers are key components of many high performance systems such as FIR filters, Microprocessors, Digital Signal Processors, ALU etc. A system’s performance is generally determined by the performance of the multiplier as the multiplier is generally the slowest element in the system and generally consumes more area and power and long latency. Therefore, low-power multiplier design has been an important part in low-power VLSI system design. An nxn multiplication is conventionally composed of three operational phases: Partial product generation, Carry-free reduction of partial products and Carry propagating addition. The PPR phase has been the subject of most research and design efforts on parallel multipliers mainly because it is the most area and power consuming part among the three. The parallel PPG is normally a constant time operation, while the minimum latency of partial product reduction (PPR) and CPA are both of the order of log n. speeding up the addition of partial products required faster adders. The major problem with fast addition was carry propagation. This spurred lot of interest in the design of arithmetic circuits. |
| In general there are sequential and combinational multiplier implementations. The DSP applications not only demand great computational capacity but also consume considerable amount of energy. While performance and area remain to be the two major design tools, power consumption has become a critical concern in today’s VLSI system design. |
| The need for low-power VLSI system arises from two main reasons. Firstly, with the steady growth of operating frequency and processing capacity per chip, large currents have to be delivered and the heat generated must be removed by proper cooling techniques. Secondly, battery life in portable electronic devices is limited and low power design directly leads to prolonged operation time. Extensive work is being carried out on low power multipliers at technological, physical, circuit and logic levels and as a result, several parallel multipliers are designed with different area-speed constraints. |
EXISTING SYSTEM |
| Booth multiplier is a multiplier which multiplies 2 signed integers in 2's complement. The algorithm is depicted in the following Figure with a brief description. The approach uses fewer additions and subtractions than more straightforward algorithms. The block diagram of Booth Multiplier is shown in figure 1. |
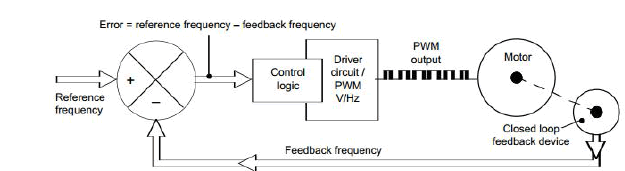 |
| Figure 1: Hardware architecture of Booth multiplier. |
| a)BOOTH ALGORITHM |
| Traditional hardware multiplication is performed in the same way multiplication is done by hand: partial products are computed, shifted appropriately, and summed. This algorithm can be slow if there are many partial products (i.e. many bits) because the output must wait until each sum is performed. Booth’s algorithm cuts the number of required partial products in half. This increases the speed by reducing the total number of partial product sums that must take place. |
| Booth algorithm gives a procedure for multiplying binary integers in signed 2's complement representation on. It operates on the fact that strings of 0's in the multiplier require no addition but just shifting and a string of 1's in the multiplier from bit weight 2k to weight 2m can be treated as 2K+1-2m. |
| The algorithm exploits the fact that multiplication by a sequence of 1’s can be computed simply with inversions and shifts, simpler operations than adding. This algorithm first encodes the start, middle, end, or absence of a sequence of 1’s in the multiplier term from groupings of three bits, each with an overlapping bit from the previous grouping. These encodings are then used to compute the partial products from the multiplicand by either multiplying it by 1 (i.e. no change), multiplying it by 2 (shift left one bit), or multiplying it by -1 (2’s complement). The encodings are shown in Table 1. These partial products are shifted by two bits for each partial product after the first. The product is equal to the sum of these terms. |
| b)BOOTH ENCODER |
| Booth multiplication is a technique that allows for smaller, faster multiplication circuits, by recoding the numbers that are multiplied. It is possible to reduce the number of partial products by half, by using the technique of radix-4 Booth recoding. The basic idea is that, instead of shifting and adding for every column of the multiplier term and multiplying by 1 or 0, we only take every second column, and multiply by ±1, ±2, or 0, to obtain the same results. The advantage of this method is the halving of the number of partial products. To Booth recode the multiplier term, we consider the bits in blocks of three, such that each block overlaps the previous block by one bit. Grouping starts from the LSB, and the first block only uses two bits of the multiplier. Figure 2 shows the grouping of bits from the multiplier term for use in modified booth encoding. |
 |
| c)PARTIAL PRODUCT GENERATOR |
| Partial product generator is the combination circuit of the product generator. Product generator is designed to produce the product by multiplying the multiplicand X by 0, 1, -1, 2 or -2. For product generator, multiply by zero means the multiplicand is multiplied by “0”. Multiply by “1” means the product still remains the same as the multiplicand value. Multiply by “-1” means that the product is the twoâÃâ¬ÃŸs complement form of the number. Multiply by “-2” is to shift left one bit the twoâÃâ¬ÃŸs complement of the multiplicand value and multiply by “2” means just shift left the multiplicand by one place. |
| d)FOUR TO TWO COMPRESSOR |
| 4:2 compressors are basic components in the design of parallel multipliers. Low power consuming 4:2 compressors can result in a significant reduction of power when realizing power-efficient multipliers in any low power oriented systems. In the area of low power integrated circuit design, adiabatic switching technique has received considerable attention in the recent years. Many adiabatic logic architectures have been reported. An FTC is functionally equivalent to two cascaded full adders (FAs) in the sum path, but there are special FTC implementations that show 25% less latency (measured in gate level delay) than that of two cascaded FAs. |
 |
| Fig 3:FTC (a) Block diagram (b) Architecture |
| A 4-2 compressor consists of five inputs and three outputs. It is called compressor, since it compress four partial products into two. This can be implemented with two stages of full adders (FA) connected in series as shown in Figure 3. The structure actually compresses five partial product bits into three, however it is connected in such a way that four of the inputs are coming from the same bit position of the weight j while one bit is fed from the neighboring position j-1 (known as carry-in). The output of such a 4:2 module consists of one bit in the position j and two bits in the position j+1. The input variables in Figure 2.5 are denoted by x1, x2, x3, x4, and ci. The variables ci is the co generated by the preceding stage. The design of 4-2 compressor is based on modified set of equations for the cout, sum and carry outputs as: |
 |
PROPOSED SYSTEM |
| The Block diagram of proposed multiplier is shown in figure 4. It Consists of a Two’s Complement Generator, Modified Booth Encoder, Partial Product Generator, and FTC. |
 |
| Fig 4:Block Diagram of Proposed Booth Multiplier |
| a)MODIFIED BOOTH ENCODER |
| The Modified Booth Encoder (MBE) The encoder generates signals by encoding the three xsignals. The yLSB signal is the LSB of the y signal and is combined with x-signals to determine the Row_LSB and the Neg_cin signals. The new scheme presented here is the fastest design with good area performance. To examine the effects of applying the new MBE scheme, the delay profiles for each design are compared. |
| b)LOW POWER FTC |
| A low power FTC using 8T full adder have been used to implement the Multiplier. These full adders have been implemented using two number of 3T XNOR gate in cascade and the carry output has been implemented using 3T XNOR gate and 2T multiplexer. The performance of 4-2 compressor has been analyzed to verify the performance of 1-bit full adder in complex VLSI circuitry. The schematic and layout design of 4-2 compressor using existing 8T full adder are shown in Figure 6. |
 |
| MULTIPLIER PERFORMANCE AND COMPARISON |
| When performance of circuits is compared, it is always done in terms of circuit speed and size. A good estimation of the circuit’s size is to count the total number of gates used. The physical delay of circuits originates from the small delays in single gates, and from the wiring between them. The delay of a wire depends on how long it is. Eventually when the number of devices is reduced the length of wires can be decreased. The device count of MBE is considerably less than the conventional encoder. |
| The performance parameters taken for analysis are power and delay and the parameters are compared and tabulated as follows. |
Comparison of conventional and Modified Booth Encoder |
 |
| Table 1: Comparison between Conventional and modified booth encoder |
| From the result obtained it is seen that the power and delay for Modified Booth Encoder is less than conventional Booth encoder. |
Comparison of conventional and modified Booth multiplier |
 |
| Table 2: Comparison between Conventional and modified booth multiplier |
| From the comparison it is found that Modified Booth Multiplier is efficient in terms of power and delay than the conventional multiplier. |
CONCLUSION |
| The new MBE scheme is proposed that utilizes lesser number of gates and eventually reduction in power is obtained. The utilized four to two compressor provides a circuit which consumes less power, area and delay. From the simulation results, the power analysis and delay analysis of each circuit are made for various circuits. The result shows that proposed MBE scheme can achieve significant improvement in power consumption. The multiplier can be extended for higher order bits. Further work can be carried out by still optimizing the power consumption and delay of the architecture by reducing the number of partial products. |
References |
|