ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S.Ananthi1, G.Ramprabu1, R.V.Anisha2, M.Chandralekha2 and D.Heera2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, we implement transmit antenna selection to enhance the energy efficiency of large scale multiple antenna systems. Two easy but effective antenna selection algorithms, Sequential Search Algorithm (SSA) and Binary Search Algorithm (BSA) are proposed to obtain the maximal energy efficiency. In addition, BER performance is determined using non-linear receivers which integrate minimum mean-square error equalization with successive interference cancellation. The simulation results show MMSE-SIC detection technique exhibit 40% better BER performance than ZF-SIC and MRC-SIC.
Keywords |
| Large scale multiple antenna system, transmit antenna selection, energy efficiency, selection algorithms, successive interference cancellation |
INTRODUCTION |
| In the recent years, —Multiple antenna wireless systems have attracted more scrutiny as it improves system performance by increasing the count of transmit and receive antennas at the price of higher hardware costs and computational burden. To overcome the hardware complexity, antenna selection scheme have been approached [3]–[4]. The disadvantage of employing more antennas lead to complexity as separate radio frequency (RF) chains are attached to each antenna. It in turn hikes up the implementation cost. From [4], Fast algorithms are proposed to select optimal no of transmit antennas to reduce complexity and parameters such as capacity are taken into consideration .In other case, from [3], antenna subset selection has been accounted by criteria such as maximum mutual information, bounds on error rate in a noisy channel. |
| The growing demand for energy efficiency has been studied more in power related applications. In accordance with transmit antenna selection in large scale multiple antenna systems, energy efficiency have been widely discussed in [1].This paper analyzes the concept of channel hardening and various scenarios where 1)transmit power is dominates circuit power when it is smaller or negligible and 2)high circuit power for low transmit power. Taking into account the above conditions, two simple algorithms are proposed to achieve maximum energy efficiency. |
| In this paper, we focus on the two energy efficient antenna selection algorithm, Sequential Search Algorithm (SSA) and Binary Search Algorithm (BSA) to achieve maximum energy efficiency. In extension to that, the bit error rate (BER) performance of the energy efficient system is calculated using minimum mean square error and successive interference cancellation (MMSE-SIC) detection .The simulation results of BER performance compared with other equalizers enhances the point that MMSE-SIC detection is more desirable. |
| The rest of the paper is arranged as follows. Section II presents the system model In Section III, energy efficiency and two selection schemes are discussed. Simulation results are given in Section IV. Section V summarizes the paper. |
SYSTEM MODEL |
 |
ENERGY EFFICIENCY AND SELECTION ALORITHMS |
A) ENERGY EFFICIENCY |
| The energy efficiency is defined as the spectral efficiency divided by the total power consumed. It is written from [1] as |
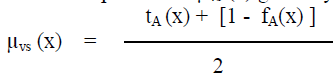 |
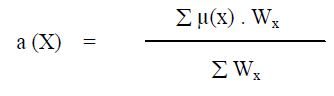 |
B) SELECTION ALGORITHM |
| As is stated in section I, many fast algorithms have been proposed to reduce the complexity [3]–[4] with the RF chains attached. From [1] we know that for a fixed transmit power, it is not necessary to employ all the available RF chains. Based on the above conclusions, the two efficient selection algorithms concentrates on the number of employed antennas and the antenna subset is stated below. We assume perfect CSI at the transmitter throughout the implementation of both algorithms. |
1) Sequential Search Algorithm (SSA): |
 |
| The sequential search is a method for finding a particular value in a list that checks each element in sequence until the desired element is found. Here the sequential search is used to find the ideal antenna subset. After every loop, the current ideal subset is represented as U1.The antennas with best channel conditions are added to the ideal subset and updated after each comparison. If Rch chain constraint is equal or more than the no of elements in ideal antenna subset (U1),then the algorithm terminates. If Rch constraint satisfied, then at every loop, a best antenna is selected from the complimentary set of U1 , U1 C to create a new set U1 '.A If condition is added to check whether the efficiency of U1 ' is smaller than or equals to the efficiency of U1 . The condition satisfies means, set U1=U1 ’ or else the search stops and ideal antenna subset is taken as U1. |
2) Binary Search Algorithm (BSA): |
 |
| The BSA is used to determine the position of a specified value within a sorted array. This algorithm requires far fewer comparisons than a linear search especially for large arrays. The location of the maximum value is taken from the middle value. |
| The low value, high value and mid value stands for lower constraint of antennas, higher constraint of antennas and midpoint of lower constraint and upper constraint of antennas respectively. Set opening value of low value and high value as 1 and Rch. The mid value is calculated by taking average of both high and low value. To find the subset in which the maximum value location is, the efficiency of (mid value+1) is compared with the efficiency of mid value. If Ãâ°Ã³(mid value+1) is more; the location is in lower constraint of antennas, set high value=mid value to check lower subset. Otherwise the location will be in upper constraint of antennas, set low value=mid value +1 to check upper subset. The mid value is updated after every loop. If the condition (high value - low value=1) is satisfied, then the maximum value location is in the mid value constraint of antennas. |
SIMULATION RESULTS |
 |
| The figure [3] shows the relationship between the average no of comparisons and transmitted power for fixed Rch chains in ideal selected antennas |
| From the figure [3], we can observe that SSA takes more no of loop comparisons to determine the ideal antennas than BSA. the complexity of SSA is proportional to the ideal number of selected antennas. Such complexities of SSA are intolerable by large arrays. Hence BSA is the most preferred algorithm. |
 |
| From fig [5], different detection techniques’ BER performance is plotted in Rayleigh channel at receiver side for QPSK modulated optimal no of selected antennas L=2 at the transmitter. As perfect CSI is considered, Zero forcing has better BER performance than typical MMSE, MRC detectors. |
 |
| From figure [6], we can perceive that conventional MMSE combined with successive interference cancellation has better BER performance than other detectors (ZF, MRC) using successive interference cancellation (MMSE-SIC). From the fig [5] and fig [6] ,we can examine that MMSE-SIC reduces error rate of MRC, MMSE and ZF by 25%,16% and 40% respectively and ZF-SIC and MRC-SIC by 40% at a constant SNR of 10 db. |
CONCLUSION |
| By using Transmit Antenna Selection, an energy efficient large scale antenna system has been developed. In extension to that, BER was determined using MMSE-SIC detection. From the simulation results, we can observe MMSE-SIC outperforms than MRC-SIC and ZF-SIC by 40% and MRC, MMSE and ZF by 25%, 16% and 40% respectively. Hence we can conclude that antenna selection and MMSE-SIC detection can be a good choice to constitute energy efficient and more reliable MIMO system. |
References |
|