ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Venkanna Mekala1 and Karuna Sagar Dasari 2 1Department of Science and Humanities, Aurora’s Engineering College, Bhongir, Hyderabad, India 2Department of Physics, Nizam College, Osmania University, Hyderabad, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The coherent edge-response of aberrated optical systems apodised with amplitude filters has been studied theoretically. The two most common problems encountered in the coherent-imaging techniques are speckling and edge-ringing. The pronounced effects of edge-ringing associated with coherent images of straight edges can be considerably reduced using variable apodisation technique. It is found that this type of apodisation is more effective not only in trimming the ringing-effect and also improves another image quality assessment factor edge gradient perceptibly which improves the edge images under the influence of defocus and primary coma. Studies on this subject indicate the importance of coherent imagery in areas like spatial filtering technique and microscopy
Keywords |
| Coherence, Edge objects, Aberrations, Imaging systems, variable apodisation |
INTRODUCTION |
| Imaging of coherent edge objects has assumed a significant role in the field of image science ever since the advent of lasers. Edge-ringing is measured by the height of the first intensity peak above the average irradiance of unity [1]. The term "ringing" is most often used for ripples in the time domain, though it is also sometimes used for frequency domain effects. It is the visual obstruction and has to be minimized by some means. Edge gradient is the increase in the image intensity per unit change in Z around the geometrical edge, i.e., at Z = 0 [2]. The gradient of the straight edge image is affected by both the amplitude transmittance and aberration of the optical imaging system. |
| In order to improve the results of an optical system, there are two methods namely modification of the optical system and post detection processing. The former involves choosing an optimum optical system itself and later involves operations on the system’s output. In many situations followed the first one by changing the pupil function with suitable apodisation. Apodisation is the technique that modifies the imaging properties of an optical system such that the system impulse does not show ringing by manipulating its entrance pupil [3]. In the present work an attempt has been made to surmount the problem of edge-ringing and improving edge-gradient in the image of straight opaque edges in coherent illumination by using variable apodisation method with the use of two different filters for various zones of transmission. These investigations have suggested the use of certain pupil functions in conjunction with optimal apodizers to trim down the edge-ringing problem [4-10]. This work presents the analytical studies carried out for variable apodisation in the case of circular apertures shaded with Lanczos filters and shaded apertures. |
II.THEORY |
| An opaque straight edge is one which is bright on one side of a line and dark on the other. |
 |
| The mathematical representation of amplitude transmission of an opaque straight edge is given by |
| A (u, v) = 1 for u ≥ 0 |
| A (u, v) = 0 for u < 0 (1) |
| This indicates that the transmission function is discontinues at u = 0. The Fourier transform for this equation gives the amplitude spectrum of the object and is given by [11] |
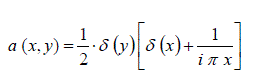 (2) (2) |
| Where δ(x)is the Dirac-delta function. The modified object amplitude spectrum at the exit pupil of the optical system is given by |
| where f(x,y) is the pupil function of the optical system. For the given optical system the complex amplitude distribution in the image plane is given by the inverse Fourier transform of expression (3). Thus |
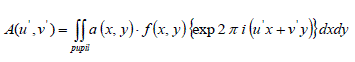 (4) (4) |
| The present work constitutes one-dimensional edge condition and hence, the general form of amplitude distribution is given by |
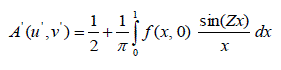 (5) (5) |
| Where |
| On introducing wave aberrations such as defect-of-focus and primary coma expression (5) takes the form |
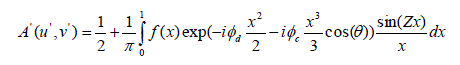 (7) (7) |
| When the given circular aperture is shaded with two amplitude filters over two zones successively, the expression (7) becomes |
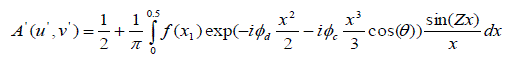 |
 (8) (8) |
| Where ‘r’ is the normalized distance of an arbitrary point on the pupil from its centre and ‘β’ is the apodisation parameter. The term β controls the degree of non-uniformity of transmission over the pupil. A value of β = 0, corresponds to diffraction limited Airy system having uniform transmission of unity over the entire aperture. |
| Now the intensity distribution of an edge image formed by a variable apodised optical system is given by the squared modulus of expression (8). |
| The investigations on the effects of defocus and primary coma on the images of edge objects formed by coherent optical systems apodised by the two amplitude filter shaded over different zones of the circular aperture have been evaluated using the expressions (9) by using Matlab7.8. The intensity distribution B(Z) in the images of straight edge objects have been obtained for different values of dimensionless diffraction variable Z varying from -3 to +20. The image quality assessment parameters such as edge-ringing (E.R) and edge-gradient (E.G) have been studied for various values of apodisation, defocus and primary coma. |
III.RESULTS AND DISCUSSIONS |
| Fig.2 shows the intensity distribution profile for circular aperture shaded with two filters f(x1) = sin(πβx)/(πβx) and f(x2) =1-πβx2 over the limits from 0 to 0.5 and 0.5 to 1 respectively for c ∅ =π and Fig.2 illustrates the case where defocus parameter d ∅ =2π with the same primary coma parameter c ∅ =π. The apodisation parameter considered are β=0, 0.25, 0.50, 0.75 and 1.00. However the value β=0 represents the clear aperture. |
| From the intensity distribution curves, it is clear that the edge ringing is the maximum in the case of clear aperture (Airy case). This is true for all values of d ∅ (i.e., for 0, π/2, π, 3π/2, 2π). From fig.2 it is observed that by the operation of apodisation the unwanted ringing has been reduced along with edge gradient. Fig.3 shows at defocusing plane d ∅ =2π the ringing is increased, however, it is decreased along with an improvement in edge gradient with β, which is desirable for an optimum optical system. |
INTENSITY PROFILES |
 |
 |
| The dependence of the edge ringing and edge gradient have been studied in detail for different values of apodisation in the presence of defocus and primary coma. Fig.4 shows that the edge ringing increases with defocusing parameter d ∅ for fixed value of β. But decreases with apodisation parameter β, for given value of d ∅ . This trend is continuing for all values of d ∅ = 0, π/2, π, 3π/2 and 2π. The edge ringing is the maximum when d ∅ =2π and β=0 and it is the minimum when d ∅ = 0 and β=1. These maximum and minimum values of edge ringing are 0.488271 and 0.308617 respectively. |
VARIATION OF E.R AND E.G WITH APODISATION PARAMETER β |
 |
 |
| It means that the edge ringing can be minimized by the operation of variable apodisation in the presence of defocus and primary coma. From the Fig.5 it is found that the edge gradient is decreasing with β for d ∅ = 0, π/2 values and it is in increasing trend for values of π, 3π/2 and 2π, i.e., as the amount of defocusing increases the gradient of edge images first decreases then increases with apodisation parameter. This effect of increase in edge gradient improves the quality of edge images. |
IV.CONCLUSIONS |
| The variable apodisation with the use of two different filters for various zones of transmission is studied and it is found that this type of apodisation is useful in reducing the ringing effect and also there is a perceptible increase in the edge gradient. The unwanted edge ringing is found to reduce even in the presence of defocus and primary coma aberrations with the apodisation parameter. For d ∅ = π, 3π/2, 2π and c ∅ =π the edge ringing shows a decreasing trend along with an improvement in edge gradient. Thus these planes may be designated as an optimum receiving image planes. |
| Hence this type of filtering technique is found to be effective in reducing the effect of coma at certain defocused planes and enhancing the resolving power aspects of edge imaging characteristics of optical systems. |
ACKNOWEDGEMENT |
| The Authors wish to thank Dr. K. Sampath Kumar Head Dept of Applied Statistics, Telangana University, Nizamabad for his continuous technical assistance. |
References |
|