ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Swapnil N. Dhande1, Y. R. Suryawanshi2 and Pravin S. Patil3
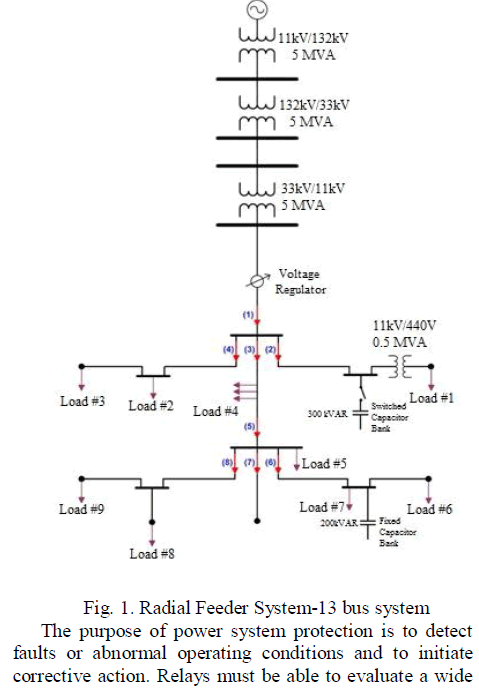
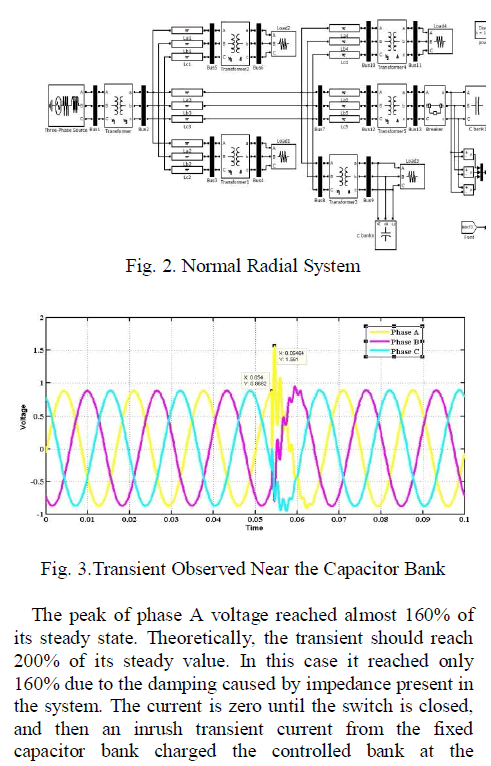
|
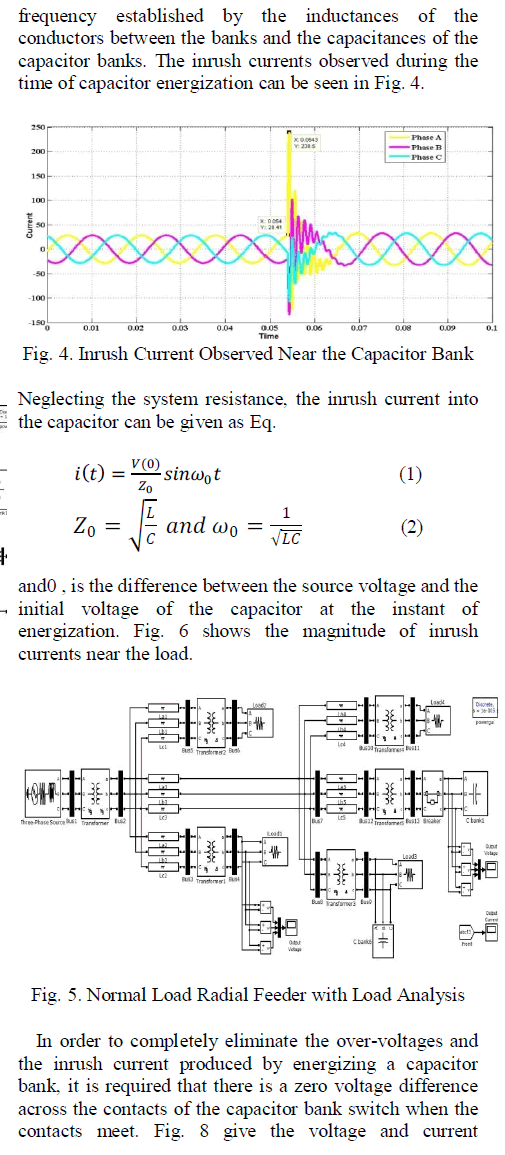
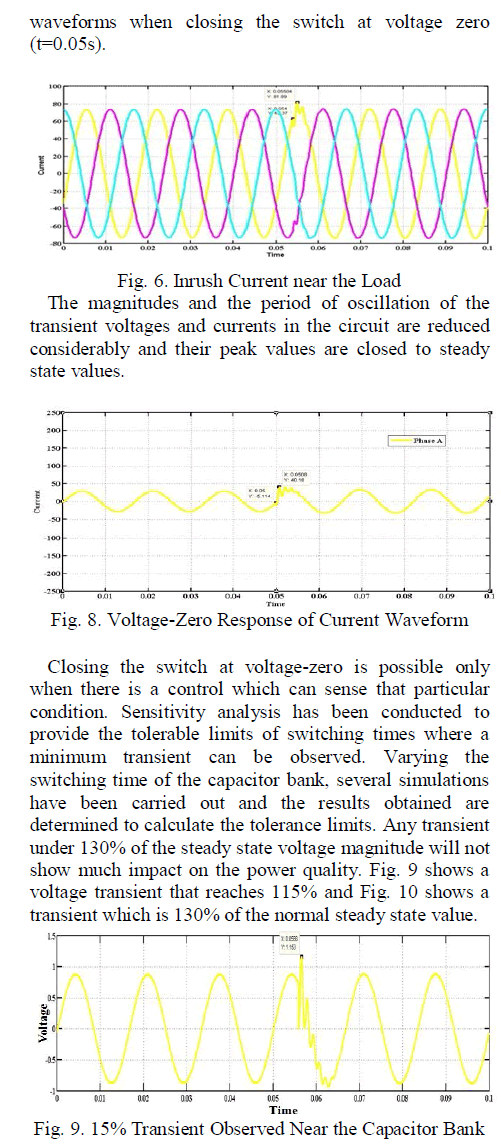
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The structural system of the building has to support the lateral loads due to earthquake and wind in addition to gravity loads. A lateral load develops high stresses and produces sway causing vibration and drift. If the buildings are not designed to resist the lateral loads, then they may be collapse resulting into the loss of life or its content. Therefore it?s important for the structure to have not only sufficient strength against gravity loads but also the adequate stiffness to resist lateral forces. Literature review reveals that LLRSS (Lateral load Resisting structural system) is provided in the form of devices like base isolation and dampers which controls the seismic vibration and lateral drift. But these devices are very costly and effective only for high rise buildings. Hence there is a need to study the LLRSS or technology suitable for a particular height of building. The objective of this research is to propose simple but innovative and effective LLRSS or structural technology and methodology for the seismic control which can be used in new as well as old building structures. It is reviewed that since North earthquake (1994), concentrically braced steel frame has gained the popularity as a LRSS in the seismic areas. In spite of increasing popularity, analytical study of braced frame structure and its detailed requirement to control the seismic response is limited in India. Also RC building involves heavy dead load due to large member size which intern is more prompt for seismic loss. Hence, it is proposed to study the response of steel buildings/frames with different types of steel bracings configurations as a LLRSS to control the vibration and storey drift. The structural response parameters selected for the study are time period, natural frequency, and roof displacement. The research work deals with the parametric study of response of Non-linear time history analysis (NLTHA) of 3D industrial steel buildings braced with different bracing configurations using software (Sap-2000) under Bhuj earthquake. The bracing configuration used are SDB, CDB, VVB and INVB in concentric bracing to suggest suitability of particular bracing configurations for the stability of the building structure under seismic loading.
Keywords |
| Seismic behaviour, Linear and non linear time history analysis, Response spectra, Bracing system. |
INTRODUCTION |
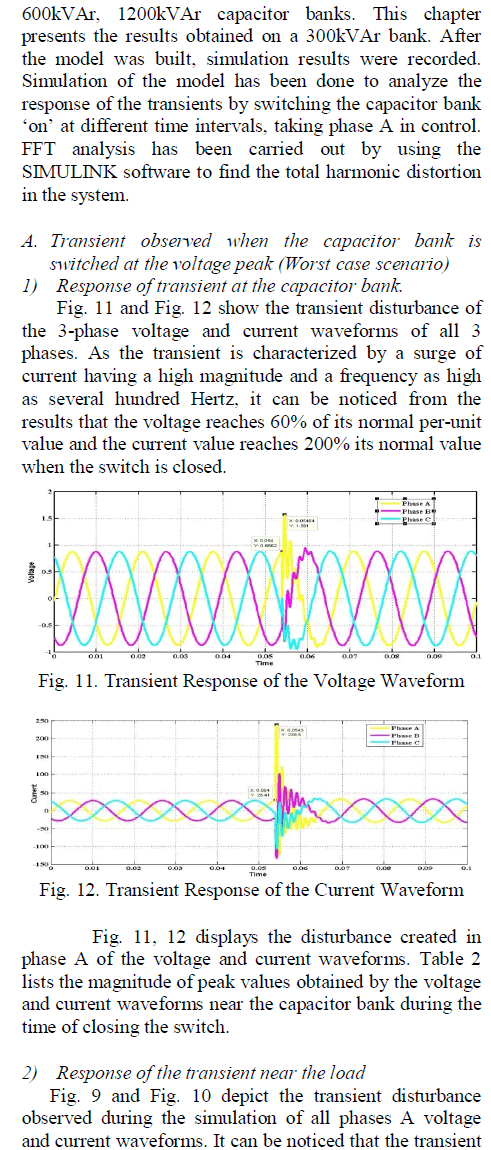
| Earthquakes are natural phenomena, which cause the ground to shake. The earth„s interior is hot and in a molten state. As the lava comes to the surface, it cools and new land is formed. The lands so formed have to continuously keep drifting to allow new material to surface. According to the theory of plate tectonics, the entire surface of the earth can be considered to be like several plates, constantly on the move. These plates brush against each other or collide at their boundaries giving rise to earthquakes. Therefore regions close to the plate boundary are highly seismic and regions further from the boundaries exhibit less seismicity. Earthquakes may also be caused by other actions such as underground explosions. The study of why and where earthquakes occur comes under geology. The study of the characteristics of the earthquake ground motion and its effects on engineered structures are the subjects of earthquake engineering. In particular, the effect of earthquakes on structures and the design of structures to withstand earthquakes with no or minimum damage is the subject of earthquake resistant structural design. The secondary effects on structures, due to floods and landslides are generally outside its scope. The recent earthquake in Kutch, Gujarat on 26 Jan 2001 has not only exposed the weaknesses in the Indian construction industry but also the lack of knowledge about earthquake engineering among all concerned. Taking advantage of the fear caused by the earthquake in the minds of both the common people and the engineering community, a number of people who have no knowledge about earthquake engineering have made totally absurd statements with regard to earthquake resistant design. Earthquake load differs from other loads in many respects, which makes it more difficult to design for it. An important characteristic of earthquake loading is the uncertainty associated with its amplitude, duration, and frequency content. Structures are normally designed to withstand gravity loads acting vertically with adequate factor of safety. Therefore the lateral loads arising due to horizontal earthquake ground motion can cause severe damage unless special provisions are made to resist them the third characteristic of earthquake ground motion is that it is cyclic and induces reversal of stresses. Therefore axially loaded members may have to resist both tension and compression while beam cross-sections will have to resist both positive and negative bending moments. The fourth characteristic is that the loading is dynamic and produces different degree of response in different structures. Dynamic analysis requires the consideration of inertia and elastic forces as well as energy dissipating mechanisms like damping (Clough and Penzien 1993). These characteristics make seismic analysis and design extremely difficult and time consuming and so simplified procedures are often used in practice. |
RELATED WORK |
| Base isolation system: It consists of placing pads between the foundation and superstructure. These pads are intended to introduce energy absorption capability to the structure, as well as flexibility to lengthen its natural time periods, therefore providing an isolation effect and reducing floor acceleration. The different types of bearing pads include lead rubber bearings, high damping rubber bearings, electrometric bearings pads and sliding friction bearings. Several buildings have adopted this method of seismic control in the united states ,Japan, New Zealand and China and these system have been found to be very effective, reducing the force transmitted from ground the structure to one half or even one third of the original value. It reduces the cost of the building by 5% to 10% compared to the traditional fixed based construction. The first application in the united states was in the Footthill communities law and justice centre in Rancho Cucamonga, California, which was completed in 1985 and include a system of 98 multilayer natural rubber bearings reinforced with steel plates. A major drawback of this control strategy is its ability to create large over turning moments at the base of the structure, which may be responsible for serious instabilities. |
| Paul [3] proposed that the dampers can be provided in the building structure to control the seismic response by its damping and flexibility. Hence depending upon the situation, structure can be damped with dampers alone or can be braced using dampers. |
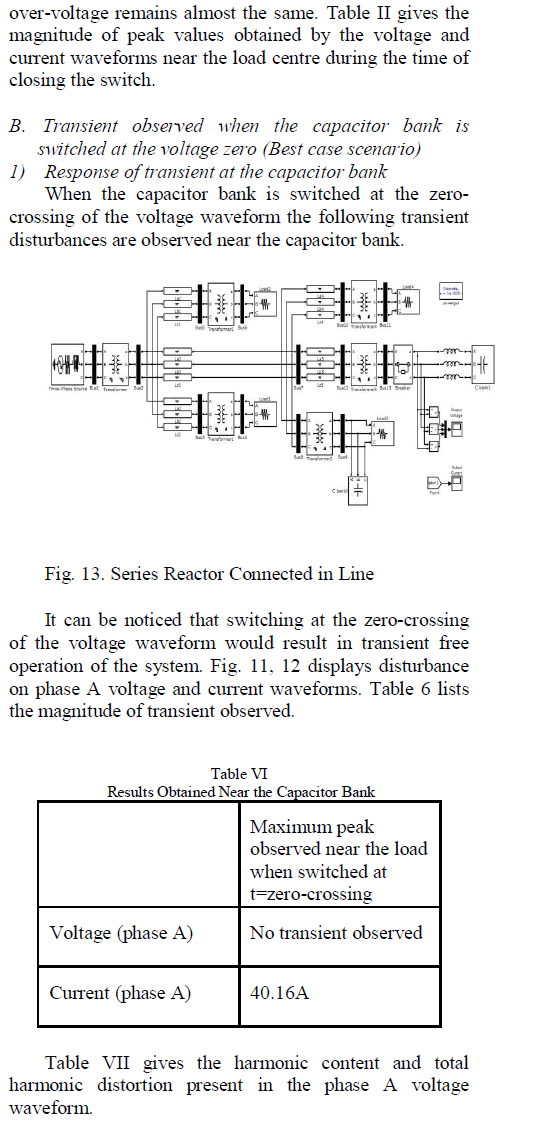
| Mahmoodi [1] proposed that Viscous damper (VD) and Visco-Elastic damper (VED) systems are in use for many years VD„s which for many years have been used by military and aerospace fields, are beginning to emerge in structural engineering. These dampers possesâÃâ¬ÃŸ linear viscous behaviour, relatively insensitive to temperature changes and can be very compact in size in comparison to force capacity and stroke. Mahmoodi describe the characteristics of a double layer, constrained layer and shear VED. Gunter K Hoffmann [1] used the helical springs and viscous dampers for base isolation for three dimensional earthquake protections of whole structure. A helical spring provides definite linear flexibility In all 3D and VDs are highly effective in all degree of freedom. This system has already been successfully used for the installation of big diesel and turbo generators in seismic zones. Several companies in Japan have developed damping system based on different VE material. A viscous damping (VD) wall system has been developed by oils and sumitomo construction co. earthquake simulator tests of all full scale 4- steel frame with and without VD walls showed very large response reduction of range 60 to 75%. The acceleration observed to be in the range of 25% to 70% lower than those of the building without VD walls. |
| Wang D [5] Since 1960, welded steel moment resisting frames ( MRFs ) have been widely accepted as the best structure for earthquake resistant building. The deficiencies in this system came to light when such structure showed brittle fractures at connection after 1994 earthquake in California. Although none of the buildings collapsed, ongoing research has looked for a better alternative. This research has applied the self centring and energy dissipating connection concepts, used in prefabricated concrete structure to steel structure .It performed seismic shake table tests on abay3storey, steel plane frame model incorporating novel self centring post tensioned (SCPT) connections. This system, unlike traditional welded steel frames, implement high strength post-tensioned strands along with sacrificial yielding element in each beam-to-column connection and is particularly appealing for important buildings from an initial investment stand point. Proposed the design of self centring structural system as economical alternatives to special moment resisting frame (SMRF) used in the United States for the seismic retrofit of steel framed structures. The study of combining steel braces and concrete shear walls for seismic strengthening of existing building. Steel bracing with slotted bolted connection acts as energy aborting dampers under large earthquakes. The friction connection is made up of bolted splice plates that clamp on to the prop. As per UNIDO manual, strengthening of whole structure can be undertaken to improve its whole lateral force resistant, stiffness and ductility. This can be achieved through the addition of new structural members to increase the respective characteristics of the structure, like bracing in a frame or skeleton structure. The response of 4, 8 and 12 storey RC building frame braced with cross diagonal and inverted V type RC bracings and shear wall is observed by khaloo and Mohseni. Even through RC bracings are designed to be linear during earthquake excitations, two different kind of braced frames showed adequate energy absorption. Also, nonlinear strain energy in structural members is about 30% of total input energy in braced frames. |
| Subramanian [12] proposed that MRF may be economical for building up to 5 to 10 storey. Shear wall and braced frame system are economical up to 15 storey buildings. The height to width ratio of 8 to 10 is considered to form the effective bracing system. |
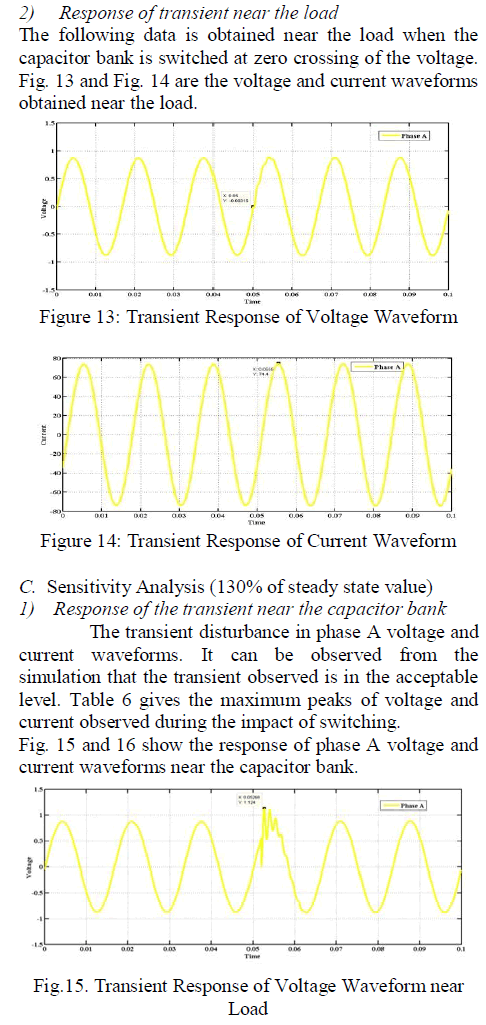
| Brad shaback ant tom brown [13] studied the behaviour of square hollow steel braces with yielding and buckling phenomenon of concentrically braced frame through pushover test. The test result indicated that the lateral rigidity of structure would decrease remarkably after the compressive braces buckled, but the horizontal bearing capacity would not decrease remarkably after compressive braces buckled, but the horizontal bearing capacity would not decrease remarkably and maintained level before buckling and ductility of concentrically steel frame was good. |
| Tomoo Saito and Haruhiko [4] presented the method of system identification in time domain which proved to be advantages than the frequency domain where modal parameter changes over the period of the record is of short duration. In this paper, dynamic characteristics, like natural frequency, time period and damping ratio for twin high rise building are estimated by applying time domain system identification method to note earthquake response. |
| Methods of analysis [14] there are several methods of analysis of structure. Accuracy and efficiency of the method, and importance and complexity of the structure decides the type of analysis/method to be used for structure. The code suggests four method of analysis of structure. Elastic (First order) analysis, plastic analysis, Advanced (second order analysis) and dynamic analysis. But fundamentally these methods consist of linear and non-linear method considering static and dynamic analysis. It is noted that many steel building in India are analysed with elastic analysis software/program only, through non-linear method are employed for important high rise building. |
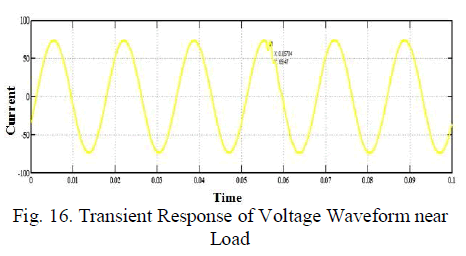
IMPLIMENTATION |
| The Lateral forces due to wind or seismic loading must be considered for tall buildings along with gravity forces. Very often the design of tall buildings is governed by lateral load resistance requirement in conjunction with gravity load. High wind pressures on the sides of tall buildings produce base shear and overturning moments. These forces cause horizontal deflection in a multi-storey building. This horizontal deflection at the top of a building is called drift. The drift is measured by drift index, Δ/h, where, Δ is the horizontal deflection at top of the building and h is the height of the building. Lateral drift of a typical moment resisting frame is shown in Fig below:- |
 |
| The usual practice in the design of multi-storey steel buildings is to provide a structure with sufficient lateral stiffness to keep the drift index between approximately 0.0015 and 0.0030 of the total height. Normally, the provision of lateral stiffness requires about 5 to 10% of extra steel. The extra steel is used for bracing systems as described in the next section. The IS code require drift index to be not more than 0.002 of total height. |
1) Lateral loading systems |
| A multi-storey building with no lateral bracing is shown in Fig. 3.2(a). When the beams and columns shown are connected with simple beam connections, the frame would have practically no resistance to the lateral forces and become geometrically unstable. The frame would laterally deflect as shown in Fig. 3.2(b) even under a small lateral load. |
 |
Shear Walls |
| The lateral loads are assumed to be concentrated at the floor levels. The rigid floors spread these forces to the columns or walls in the building. Lateral forces are particularly large in case of tall buildings or when seismic forces are considered. Specially designed reinforced concrete walls parallel to the directions of load are used to resist a large part of the lateral loads caused by wind or earthquakes by acting as deep cantilever beams fixed at foundation. These elements are called as shear walls. Frequently buildings have interior concrete core walls around the elevator, stair and service wells. Such walls may be considered as shear walls. The advantages of shear walls are (i) they are very rigid in their own plane and hence are effective in limiting deflections and (ii) they act as fire compartment walls. However, for low and medium rise buildings, the construction of shear walls takes more time and is less precise in dimensions than steelwork. Generally, reinforced concrete walls possess sufficient strength and stiffness to resist the lateral loading. Shear walls have lesser ductility and may not meet the energy required under severe earthquake. A typical framed structure braced with core wall is shown in Fig. 3.3(b). |
Braced frames |
| To resist the lateral deflections, the simplest method from a theoretical standpoint is the intersection of full diagonal bracing or X-bracing as shown in Fig. 3.6. The X-bracing system works well for 20 to 60 storey height, but it does not give room for openings such as doors and windows. To provide more flexibility for the placing of windows and doors, the K-bracing system shown in Fig. 3.5(a) is preferred instead of X- bracing system. If, we need to provide larger openings, it is not possible with K-bracing system; we can use the full-storey knee bracing system shown in Fig. 3.5(b). Knee bracing is an eccentric bracing that is found to be efficient in energy dissipation during earthquake loads by forming plastic hinge in beam at the point of their intersection of the bracings with the beam. |
 |
| Steel Bracing structures have been known to perform well under earthquake loads provided certain guidelines are followed in design. Steel being a ductile material, equally strong in compression and tension, is ideally suited for earthquake resistant structures. Bracing members are used either as part of a lateral load resisting system or to increase the stiffness of a frame in the lateral direction. They may be either pin-ended or fixed-ended. Pin-ended braces will be subjected to only axial forces and usually fail by global buckling under compressive load. After the initial buckling, the buckling strength gets reduced in subsequent cycles due to non-straightness of the brace. However, the maximum tensile strength remains relatively unchanged during cycling and presents a ductile behaviour. Therefore, pin-ended braces are usually used in pairs, as in X-bracing so that at least one brace will be effective for loading on either side. Another advantage of using braces is that it becomes possible to dissipate energy without damaging the main structure and it is easy and economical to replace the braces after an earthquake. Structures are usually designed for gravity loads and checked for earthquake loading. In conformity with the design philosophy, this check consists of two steps the first ensures elastic response under moderate earthquakes and the second ensures that collapse is precluded under a severe earthquake. Due to the uncertainties associated in predicting the inelastic response, the second check may be dispensed with, by providing adequate ductility and energy dissipation capacity. In this section, the various methods of performing these checks are described. The important factors, which influence earthquake resistant design are, the geographical location of the structure, the site soil and foundation condition, the importance of the structure, the dynamic characteristics of the structure such as the natural periods and the properties of the structure such as strength, stiffness, ductility, and energy dissipation capacity. These factors are considered directly or indirectly in all the methods of analysis. Elastic response analysis is invariably performed as a part of the usual design procedure. The primary aim of elastic analysis is to ensure serviceability under moderate earthquakes. For simple and regular structures, the seismic coefficient method is normally used. Structures such as multi-storeyed buildings, overhead water tanks and bridge piers are usually designed by the response spectrum method while for more important structures such as nuclear reactors; time-history response analysis is usually adopted. In what follows the seismic coefficient method is explained in detail while the response spectrum method and time history analysis are described briefly since understanding of these methods requires some knowledge of structural dynamics. For important structures, both linear and non-linear responses can be obtained by carrying out detailed time-history analysis for one or more design accelerograms. These design accelerograms may be either natural accelerograms recorded at the site or at similar sites or they can be artificial accelerograms generated in such a way as to be compatible with the design response spectrum. A variety of numerical time-stepping methods are available for calculating the response time-history. The Non linear Analysis First we will understand diff. between linear and non linear analysis the term “stiffness” defines the fundamental difference between linear and nonlinear analysis. Stiffness is a property of a part or assembly that characterizes its response to when the applied load. A number of factors affect stiffness such as shape of section, type of material etc. structure deforms under a load its stiffness changes, due to one or more of the factors listed above. If it deforms a great deal, its shape can change. If the material reaches its failure limit, the material properties will change. |
| On the other hand, if the change in stiffness is small enough, it makes sense to assume that neither the shape nor material properties change at all during the deformation process. This assumption is the fundamental principle of linear analysis. The modelling beam-column connection are ideally neither pinned nor fixed and posses finite-zero stiffness. However, they are classified as simple (pinned), semi-rigid (semi-pinned) and rigid (fixed) depending on the connection stiffness. Such classification helps in simplifying the analysis of frames. A connection having a small stiffness can be assumed as pinned while connection having a large stiffness can be assumed as fixed. In the former case, the actual mid span bending moment will be less than what is designed for while in the later case the mid-span deflection will be more than what is calculated. The common methods of beam-column connection in steel frame structures include welds, rivets, unfinished bolts and high strength bolts. The analysis of braced frame in this dissertation assumes proper and intact beam-column connection for MSBF without taking into account the study of type of joints as a welded/riveted/bolted (or fully simple or rigid). The types of connections are so rigid that their displacement can be neglected under normal loading condition. Despite of the rigidity of connections, the beam-column joint assemblage can nevertheless exhibit some degree of flexibility under seismic ground motion. |
| Some research has shown that the displacement of the beam-column joints can considerably affect the response of a steel frame structure. Also it is reviewed that some energy can be dissipated at the beam-column connection by the addition of energy dissipater. One of such device called as panel zones can be added to exhibit the stable hysteretic behaviour of a panel zone can be modelled in a similar way as that of a fibre, except that a different monotonic loading curve between joint moment and shear strain is used. Lateral loading during NLTHA Being the act of nature, the earthquake and wind on earth surfaces are randomly varying time dependent phenomenon; and like unwelcome guest and unavoidable. Therefore, one has to accept and understand the characteristics of these with best possible way. One has to design the structure to resist the their effect by keeping the response within the limit by adopting appropriate design measure to protect and keep humanity as comfortable as possible with less expense. The first important difference between structural response to an earthquake and response to most other loadings is that the earthquake response is dynamic and non static while for the most structures, response to wind is essential static. The forces within the structure are due almost entirely to the pressure loading rather than the acceleration of the mass of the structure. But with ground shaking, the portion of a structure above the ground is not subjected to any applied force. The stresses and strains within the superstructure are created entirely by its dynamic response to the movement of its base and the ground. The recorded building motion enables the analysis to be made of the stresses and strains in the structure during the earthquake. Even through the most used design procedure reports to the use of a concept of equivalent static force for actual calculation, knowledge of the NLTHA for building is essential. The two types of lateral loading are used during the analysis. During the study, it was observed that models subjected to wind loading have uniform response along the height due to static behaviour of lateral loading. Hence model study with earthquake as a lateral loading was continued. |
2) Description of Model:- |
| There are many combinations of parameters in the classification of industrial buildings. For the purpose of structural analysis and design. The buildings are classified in to two types such as Braced and Unbraced. In braced buildings, the trusses rest on columns with hinge type of connection and stability of the building is obtained by providing bracing in three mutually perpendicular planes and they are: |
| a) Horizontal plane at tie level of roof truss |
| b) Vertical plane along the longitudinal section of columns |
| c) Vertical planes in the end cross section usually at the gable ends. |
| Braced frames are efficient in resting loads and do not sway, however the braces introduces obstructions in some bays and cause higher forces or uplift at some places. Even unbraced building may require bracing in some directions to provide stability and minimize drifts. There could be a few more variation in skeletal structure of braced building Depending on the size of the building, functional requirement and architectural needs. |
About SAP-2000 |
| The introduction of computers and computer design models in the 1970âÃâ¬ÃŸs allowed a transition from pre-engineered rectangular building to custom-engineered structure. About 70% low-rise and non-residential buildings are the steel buildings in the united state of America (USA) and United Kingdom (108). Various computer programs are available for the analysis and design of different type of structure, the list is exhaustive. But SAP-2000 is a structural analysis program combatable with the computers and can be used for basic as well as complicated design problems. With this program. It is now possible to design and analyse any type of structure with any complicated geometry subjected to any loading (static and dynamic) and having any boundary conditions continuous and discontinues. This, this software is versatile and quite general in terms of loading, geometric configuration and support conditions and hence selected as a tool for analysis and design of the models studied in this dissertation. SAP2000 is finite element based software and uses finite element, and has been shown to stimulate damage accurately and efficiently. Modelling of the structure in the sap2000 offers various levels of sophistication and refinements. SAP 2000 provides various commands for modelling the different elements of the structure. The elements of the braced frame were modelled in the sap 2000 as per the modelling procedure discussed previously. The modelling of elements of the frame and bracings can be done with very much sophistication. The masses source used in the analysis to account for horizontally acting inertia forces was taken to be contributing from load and floor mass. As the forces from the lateral load displaces a building laterally (Δ), the gravity loads (P) acting vertically downward produces P-Δ effect, leading to global instability of the building was considered. The global P-Δ effects were considered based on the mass of the building frames. Large displacement (P-Δ) effect enabling the elements of model into inelastic behaviour was considered. Following are the salient feature of the Non-linear time history analysis (NLTHA) performed for different building models in SAP 2000. |
 |
| 6) Rise = 3.2m |
| At the bottom all joints are considered as fixed joints. |
| For the study purpose 2 models are prepared such as Gable frame-industrial building and Howe type roof truss. Steel is used and it is made up with hollow box section and different bracing configuration provided at end of truss. |
Unbraced steel structure (Gable portal frame):- |
 |
 |
Analysis for earthquake forces |
| After completing dead load analysis and modal analysis the braced industrial building is analysed for the earthquake forces, for that linear static case is considered and for each bracings the base shear and base moment is calculated to study the effects of actual earthquake on structure time history of BHUJ earthquake is applied on both braced and unbraced structures. It consists of earthquake record of every 0.005 seconds and total 30000 acceleration records are available. These records are applied as time history on the model in SAP 2000. And time history load case is defined in the software. The results of the base shear and the results of the base moment are plotted in chapter number 6. As the BHUJ earthquake forces are applied as time history, we can find the displacement of any joint with respect to time. Fig. 5.5 shows the displacement with respect to time of joint no 177 which is located at 11.2 metre height. We can observe that max displacement of joint is 0.4889 mm at 9.4 second and min displacement is 0.00055 mm at 9.6 second. |
 |
RESULTS AND DISCUSSION |
| This chapter presents the results of observation and discussion of response parameters for the various models studied in this research. Condition and modelling procedures for different models studied. The different types of bracing configuration used in the models are described. As the response of the model under different loading combinations is observed to be different, maximum response for common loading combination of 1.2 times the gravity load plus lateral load is observed. Types of lateral load used in the analysis are earthquake motion of Bhuj earthquake as per IS1893- 2002. The lateral load due to earthquake is applied directly at the base of models whereas the lateral load due to wind forces are applied statically at storey levels through the nodal points along the height of model. Multidirectional effect of lateral forces is considered in both cases. For all models, longer plan dimension is considered as major (X-direction) and shorter plan dimension which is perpendicular to the major is considered as minor (Y-direction). Thus, direction for time history becomes major if it is applied along the X-direction and minor if it is applied along the shorter direction of the model. |
| A linear or nonlinear analysis can be performed according to the need and demand of the structural behaviour for particular circumstances. Maximum lateral force, which has a quantitative effect on the linear and nonlinear responses, is one of the most important characteristics of the earthquake and wind. As the building can be considered as short or tall, it has a high risk for collapse due to lateral loads induced by earthquake and wind. Therefore its stability may have a storey displacement / drift effect which moves building laterally. As a result it is necessary to carry out the nonlinear analysis for the building analysis only assumes the small displacements and ignores the change in geometry. In nonlinear analysis, the geometry change of the structure takes account of the P-Δ effect which does not apply to linear analysis. Hence the response of building under linear and nonlinear analysis, and nonlinear analysis with and without P-Δ effect is compared. To illustrate the importance and accuracy of nonlinear time history analysis (NLTHA), two representative models are analyzed and response is investigated here. |
Effect on natural time period (T) |
| The evolution of the natural time vibration periods of the building structure is quite important in the dynamic analysis of structure. Table 6.1 shows the natural time periods of first fundamental mode for all models under the THX and with bracing provided. It is observed that time periods for all models and all bracing configuration is less than the time period of unbraced frame. Same observation made were made for the direction THY. |
 |
| IN fig 6.1(a), it is seen that all braced model reduces the roof displacement significantly as compared to unbraced model. The effectiveness of bracing in reducing the roof displacement as compared to unbraced model is INVB, VVB, CDB and SDB. In fig 6.1 (b), it is seen that all braced model increases the roof acceleration significantly as compared to unbraced model. The effectiveness of bracing in reducing the roof acceleration as compared to unbraced model is SDB, CDB, VVB and INVVB. |
 |
 |
Energy dissipation by different bracing |
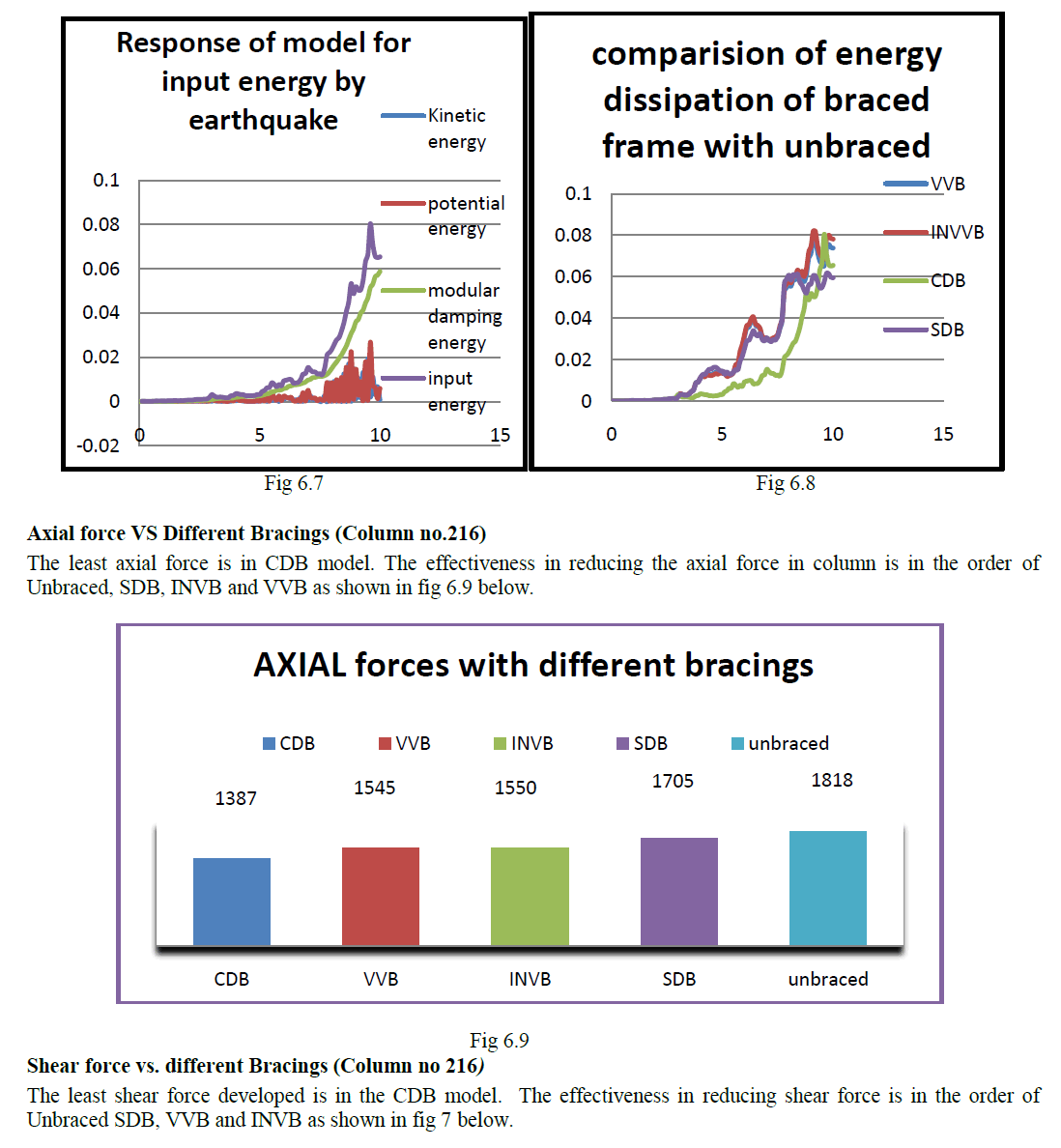
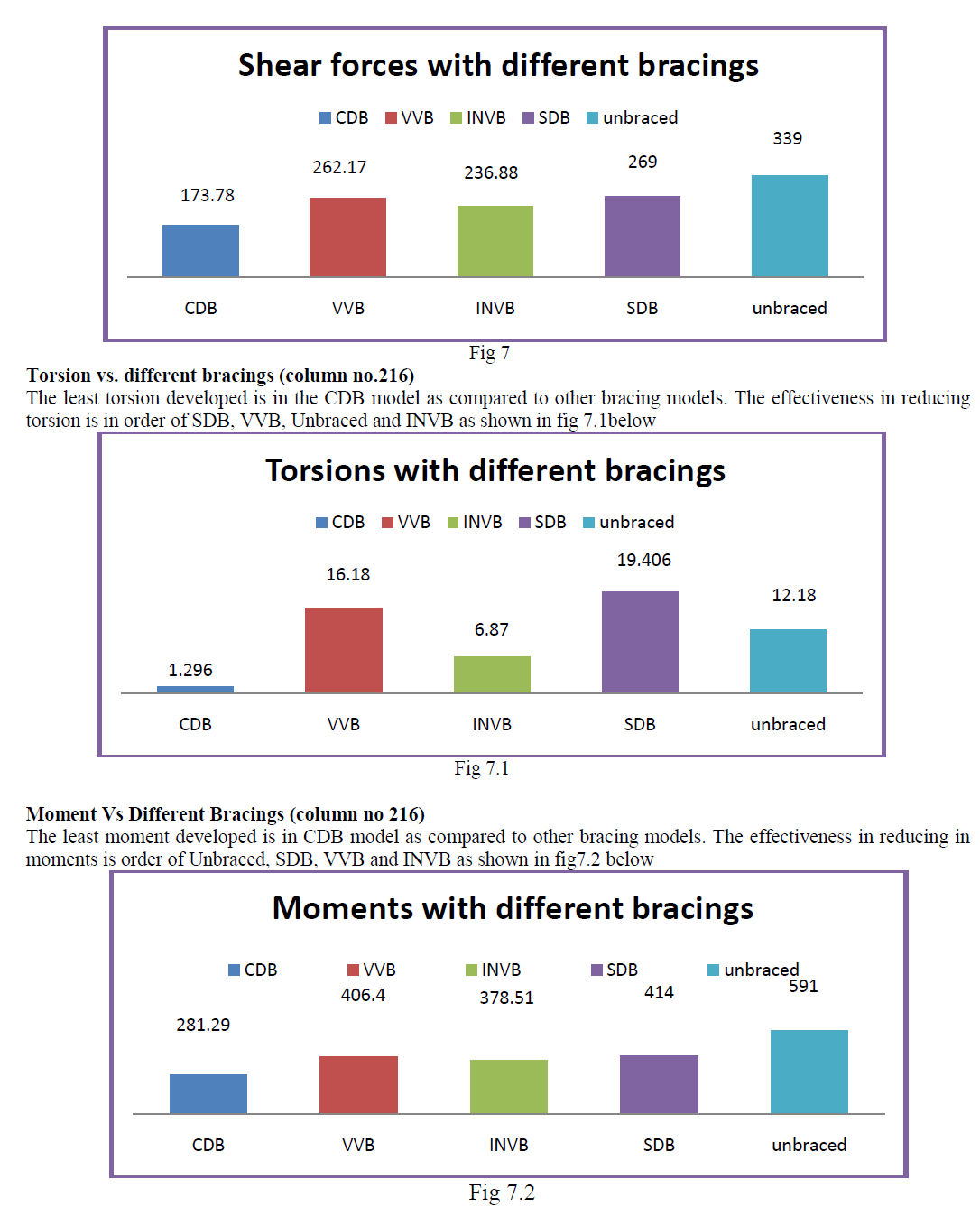
| Fig 6.7 shows the response of energy dissipation by model braced with CDB for the input energy applied by the earthquake. It is seen that braced model is able dissipate the energy input by earthquake. Fig 6.8 shows the response of energy dissipation by the truss models braced with different bracing configuration. It is seen that INVB dissipates more energy followed by SDB, VVB and CDB respectively. |
 |
 |
Base shear vs. Different bracings due to Static loading |
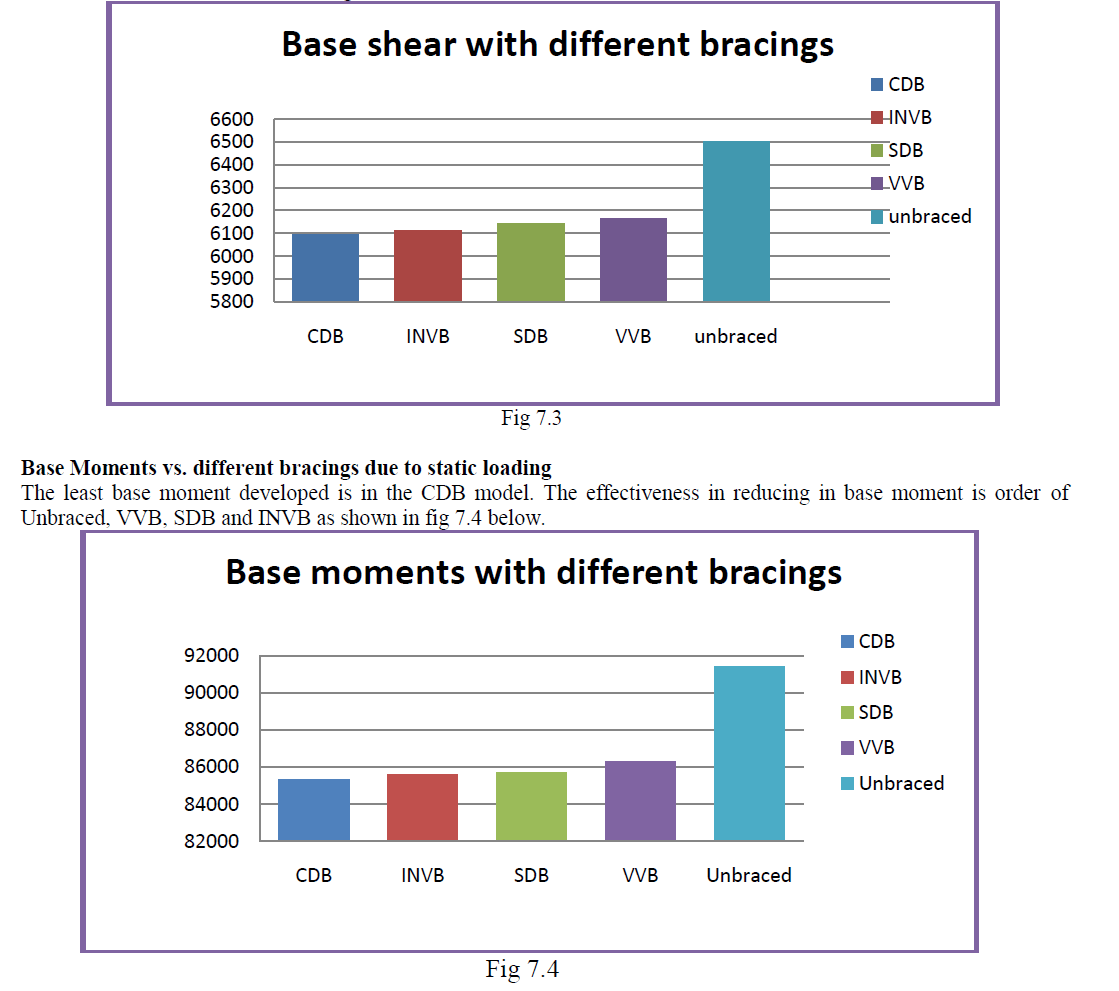
| The least base shear developed is in the CDB model. The effectiveness in reducing in base shear is order of Unbraced, VVB, SDB and INVB as shown in fig7.3 below. |
 |
| In this chapter, the responses are obtained for different building model with and without different bracing configuration namely SDB, CDB, VVB and INVB. The model has been compared for the suitability of bracing configuration with one another bracing. |
FUTURE SCOPE |
| Braces are likely to develop significant bending moments and shear forces in actual applications and the effect of this on behaviour of braced frame is unclear. An analytical study can be made to stimulate this behaviour. |
CONCLUSION |
| All bracings configuration can be used to control the response of roof displacement. Rating of bracing configurations towards the effectiveness of roof displacement control is INVB, VVB and CDB. Bracing configuration in braced frames reduces the natural time period of vibration. INVBs, VVBs and CDBs are effective next new bracing configuration. |
References |
|