ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
B.R.Sharma , Debozani Borgohain
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In the presence of chemical reaction, the Soret effect and Dufour effect on heat and mass transfer over a stretching cylinder embedded in a porous medium have been studied numerically. A set of coupled ordinary differential equations are obtained from the governing nonlinear partial differential equations which are then solved numerically by using MATLAB‟s built in solver bvp4c. The effects of material parameters like the Reynolds number, Darcy number, chemical reaction parameter, Schmidt number, Dufour number, Soret number, Prandtl number and order of the chemical reaction on temperature and concentration distributions are discussed through graphs. Also the local Nusselt number and local Sherwood number for various values of the above mentioned parameters are tabulated. It is concluded that chemical reaction parameter and order of the chemical reaction play crucial role in the solution.
Keywords |
| Heat and Mass transfer; Porous Medium; Stretching cylinder; Dufour and Soret effects; order of chemical reaction. |
I. INTRODUCTION |
| Free convection heat and mass transfer through porous media has many important applications in the field of large storage systems of agricultural products, petroleum extraction, control of pollutant spread in groundwater, solar power collectors, heat recovery from geothermal systems and porous material regenerative heat exchangers. Many researchers such as Nield and Bejan[1], Vafai[2] and Ingham and Pop[3, 4] have made comprehensive reviews in this area. In several processes, there is a great importance of chemical reactions in the combined heat and mass transfer problems and have therefore attracted a considerable amount of attention in the last several decades. Chemical reactions are either homogeneous or heterogeneous processes. The reaction is homogeneous, if it occurs uniformly through a given phase. In well mixed system, it takes place in the solution while a heterogeneous reaction occurs at the interface i.e. in a restricted region or within the boundary of a phase. If the rate of reaction is proportional to the nth power of concentration then the chemical reaction is said to be of order „nâÃâ¬ÃŸ. Chemical reaction between a foreign mass and the fluid occurs in many industrial applications such as polymer production, the manufacturing of ceramics or glassware and so on. |
II. RELATED WORK |
| A first order chemical reaction in the neighbourhood of a horizontal plate have been analyzed by Chambre and Young[5]. Das et al.[6] have discussed the effects of chemical reaction and mass transfer on flow past an impulsively infinite vertical plate with constant heat flux. The flow and mass diffusion of a chemical species with first order and higher order reactions over a linearly stretching surface have been analyzed by Andersson et al.[7]. Anjalidevi and Kandasamy[8] have studied the steady laminar flow along a semi infinite horizontal plate in the presence of a species concentration and chemical reaction. Chamkha[9] presented the analytical solutions for the overall heat and mass transfer on MHD flow of a uniformly stretched vertical permeable surface with the effects of heat generation/ absorption and chemical reaction. Rashad et al.[10] have analyzed the coupled heat and mass transfer by mixed convection about solid sphere saturated porous medium in the presence of chemical reaction effect. Jyothi Bala and Vijaya Kumar[11] have discussed the unsteady MHD heat and mass transfer by a semi infinite vertical porous moving plate in the presence of heat generation and chemical reaction. |
| In chemical engineering, Soret and Dufour effects are important for intermediate molecular weight gases in coupled heat and mass transfer in binary systems. Abd El-Aziz[12] studied the thermal diffusion and diffusion thermo effects on the heat and mass transfer characteristics of free convection past a continuously stretching permeable surface in presence of magnetic field and radiation. The influence of chemical reaction on heat and mass transfer by natural convection from vertical surfaces embedded in fluid saturated porous medium considering Soret and Dufour effects was discussed by Postelnicu[13]. The Soret and Dufour effects on natural convection heat and mass transfer from a vertical cone in a porous medium were studied by Cheng[14]. Sharma et al.[15] discussed the influence of chemical reaction, heat source, Soret and Dufour effects on separation of a binary fluid mixture in MHD natural convection flow in porous media. Wang[16] discussed the flow of the fluid due to a stretching cylinder. Chamkha et al.[17] have studied the effects of thermal stratification on flow and heat transfer due to stretching cylinder with uniform suction/ injection. The present paper deals with the two dimensional steady, laminar boundary layer flow of an incompressible viscous fluid over a stretching cylinder embedded in a porous medium in the presence of chemical reaction. The main aim of this paper is to study the influence of the order of chemical reaction, Soret effect and Dufour effects on the fluid. The present study is an extension of the work of El Kabeir[18] by considering the chemical reaction of order n and using the impervious boundary condition for concentration at the surface of the cylinder. |
III. MATHEMATICAL FORMULATION |
| Consider a two dimensional laminar, steady flow of a viscous incompressible binary fluid mixture over a stretching tube embedded in a porous medium. As shown in fig.1, the radius of the stretching tube is taken as „aâÃâ¬ÃŸ in the axial direction, the z - axis is measured along the axis of the tube and the r - axis is measured in the radial direction in a fluid at rest. The ambient temperature far away from the surface of the cylinder is T∞ and the surface of the tube is maintained at constant temperature TW such that TW > T∞. The surface of the cylinder is considered to be impervious and the concentration of the binary fluid mixture far away from the plate is considered to be C∞. It is assumed that the physical properties of the fluid mixture are constant. It is also assumed that homogeneous chemical reaction of order n takes place in the flow. |
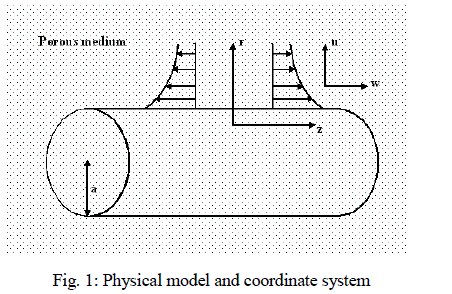 |
| Under the above assumptions, the governing equations describing the conservation of mass, momentum, energy and concentration can be written as follows: |
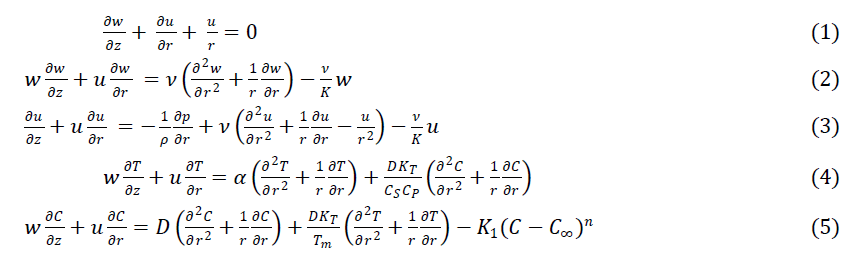 |
| where u and w are fluid velocity components along the z- and r- directions respectively, ν is the kinematic viscosity, ρ is density, K is permeability of porous medium, KT is the thermal diffusion ratio, α is the thermal diffusivity, D is the mass diffusivity, T is temperature, C is concentration, Cp is the specific heat capacity, Cs is the concentration susceptibility, Tm is the mean fluid temperature, K1 is the dimensional chemical reaction parameter, n is the order of the chemical reaction, p is the pressure. |
| The boundary conditions are |
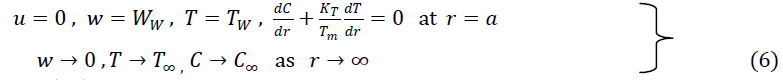 |
| where WW = 2cz, c is a positive constant |
| We now introduce the following dimensionless variables: |
 |
IV. RESULTS AND DISCUSSION |
| Numerical calculations have been carried out for various values of the parameters Re, Da, Sc, Df, Sr, Pr, γ and n. Eight cases are considered: |
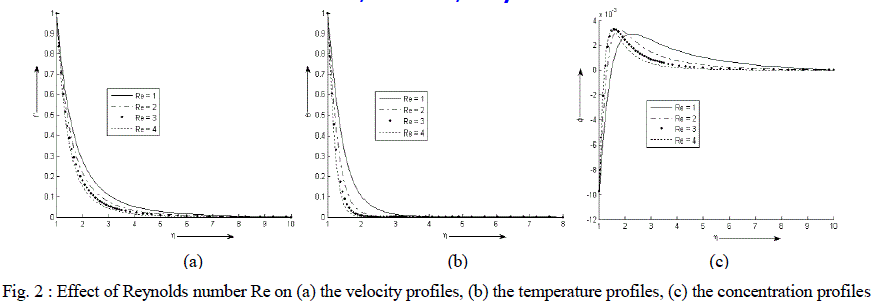
| Case I : Re = (1, 2, 3, 4), Da = 1, Sc = 1.6, Df = 0.15, Sr = 0.01, γ = 0.02, n = 4, Pr = 7 |
| Case II : Re = 1, Da = (1, 5, 10, 1010), Sc = 1.6, Df = 0.15, Sr = 0.01, γ = 0.02, n = 4, Pr = 7 |
| Case III : Re = 1, Da = 1, Sc = (0.5, 0.9, 1.6, 2.2), Df = 0.4, Sr = 0.04, γ = 0.02, n = 2, Pr = 7 |
| Case IV : Re = 1, Da = 1, Sc = 1.6, Df = (0.15, 0.4, 0.6, 0.8), Sr = 0.04, γ = 0.02, n = 1, Pr = 7 |
| Case V : Re = 1, Da = 1, Sc = 1.6, Df = 0.2, Sr = (0.01, 0.03, 0.05, 0.07), γ = 0.02, n = 2, Pr = 7 |
| Case VI : Re = 1, Da = 1, Sc = 1.6, Df = 0.15, Sr = 0.4, γ = (0.01, 1, 2.5, 4), n = 1, Pr = 7 |
| Case VII : Re = 1, Da = 1, Sc = 1.6, Df = 0.15, Sr = 0.01 γ = 0.02, n = (1, 2, 4, 6), Pr = 7 |
| Case VIII : Re = 4, Da = 4, Sc = 1.6, Df = 0.15, Sr = 0.01, γ = 0.02, n = 2, Pr = (0.7, 4, 7, 13.2) |
| The numerical results for velocity, temperature and concentration profiles are displayed in Figures (2) - (9). |
| Case I: |
| Figure 2 (a) - (c) exhibit velocity, temperature and concentration profile for various values of Re. It is observed that the velocity and temperature decreases exponentially from its maximum value at the surface to its minimum value at the end of the boundary layer. The value of the concentration of the rarer and lighter component is less near the surface than its value at the edge of the boundary layer but increases sharply, attends its maximum value at about η = 2 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also noticed that with an increase in the values of Reynolds number Re, the velocity and temperature of the binary fluid mixture decreases sharply. The concentration increases near the surface of the cylinder with an increase in the values of Re but reverse effect is observed away from the surface. |
 |
| Case II: |
| Figure 3 (a)-(c) exhibit velocity, temperature and concentration profile for various values of Da. It is observed that the velocity and temperature decreases exponentially from its maximum value at the surface to its minimum value at the end of the boundary layer. The value of the concentration of the rarer and lighter component is less near the surface than its value at the edge of the boundary layer but increases sharply, attends its maximum value at about η = 2 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also noticed that with an increase in the values of Darcy number Da, the velocity of the binary fluid mixture increases sharply while the temperature of the binary fluid mixture decreases slightly. On the other hand the concentration remains same near the surface of the cylinder with an increase in the values of Da but after attaining its maximum value at about η = 2 the concentration decreases. |
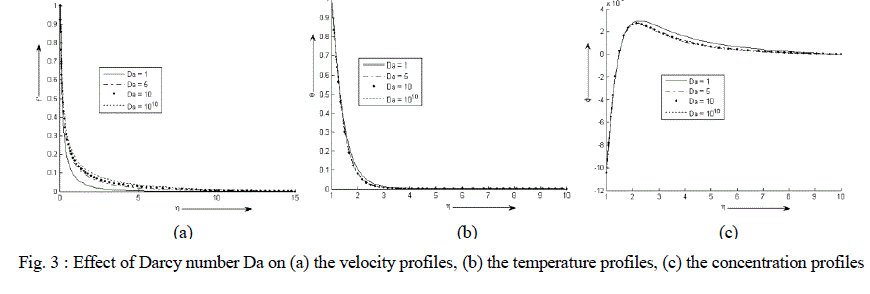 |
| Case III: |
| Figure 4 (a) - (c) exhibit velocity, temperature and concentration profile for various values of Sc. It is noticed that the velocity and temperature decreases exponentially from its maximum value at the surface to its minimum value at the end of the boundary layer. The value of the concentration of the rarer and lighter component is less near the surface than its value at the edge of the boundary layer but increases sharply, attends its maximum value at about η = 2 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also observed that the temperature of the binary fluid mixture decreases while the velocity decreases very minutely with the increase in the values of Schmidt number Sc. The concentration decreases near the surface of the cylinder with an increase in the values of Sc but the effect gets reversed after η = 1.5 i.e. away from the surface. |
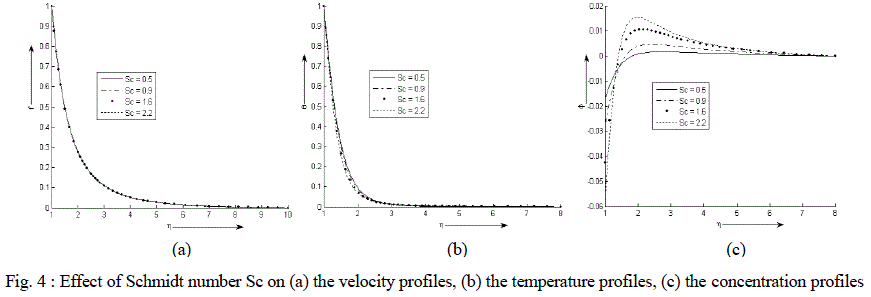 |
| Case IV: |
| Figure 5 (a) - (c) exhibit velocity, temperature and concentration profile for various values of Df. There is an exponential decrease in the velocity and temperature from its maximum value at the surface to its minimum value at the end of the boundary layer. The value of the concentration of the rarer and lighter component is less near the surface than its value at the edge of the boundary layer but increases sharply, attends its maximum value at about η = 2 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also observed that the temperature of the binary fluid mixture decreases sharply while the velocity decreases very minutely with the increase in the values of Dufour number Df. At first it is noticed that the concentration at the surface remains same but as the fluid moves away from the surface the concentration increases with an increase in the values of Df and the effect gets reversed after η = 2 i.e. further from the surface. |
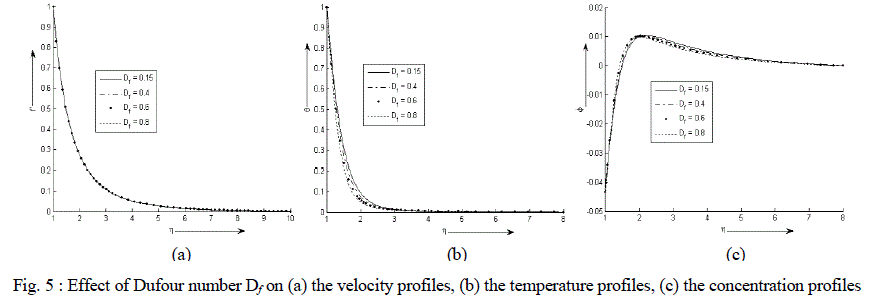 |
| Case V: |
| Figure 6 (a) - (c) exhibit velocity, temperature and concentration profile for various values of Sr. It is observed that the velocity and temperature decreases exponentially from its maximum value at the surface to its minimum value at the end of the boundary layer. The concentration is less near the surface than at the edge of the boundary layer but increases near the surface, attends its maximum value at about η = 2 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also noticed that with an increase in the values of Soret number Sr, the velocity decreases negligibly while the temperature of the binary fluid mixture decreases. The concentration decreases at and near the surface of the cylinder with an increase in the values of Sr but reverse effect is observed after η = 1.5. |
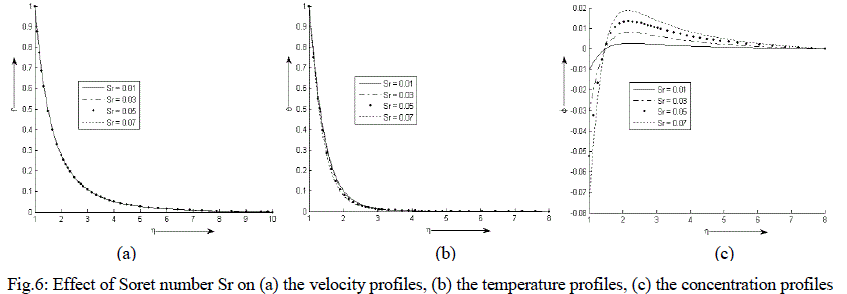 |
| Case VI: |
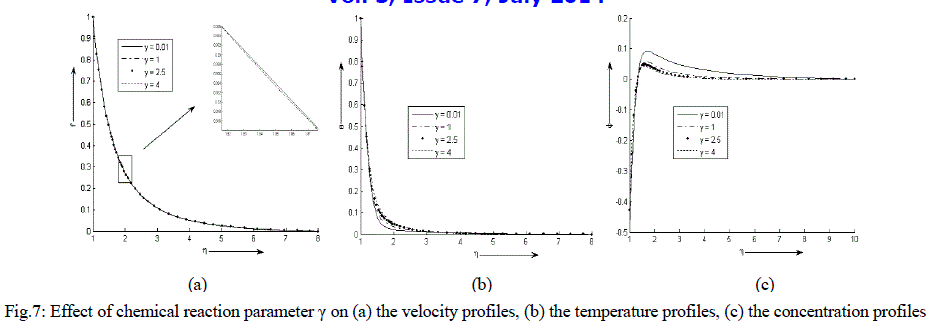
| Figure 7 (a) - (c) exhibit velocity, temperature and concentration profile for various values of γ. It is noticed that the velocity and temperature decreases exponentially from its maximum value at the surface to its minimum value at the end of the boundary layer. The concentration is less near the surface than its value at the edge of the boundary layer. It increases sharply near the surface, attends its maximum value at about η = 1.65 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also observed that the temperature of the binary fluid mixture increases while the velocity decreases very minutely with the increase in the values of chemical reaction parameter γ. The concentration is nearly same near the surface of the cylinder with an increase in the values of γ but decreases after η = 1.3. |
 |
| Case VII: |
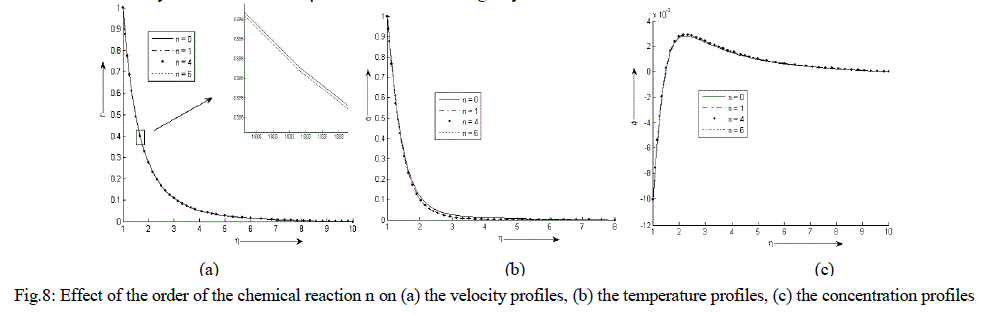
| Figure 8 (a) - (c) exhibit velocity, temperature and concentration profile for various values of n. There is an exponential decrease in the velocity and temperature from its maximum value at the surface to its minimum value at the end of the boundary layer. The concentration is less near the surface than its value at the edge of the boundary layer. It increases sharply near the surface, attends its maximum value at about η = 2 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also observed that the temperature decreases slightly while the velocity decreases very minutely with the increase in the order of the chemical reaction n. At first it is noticed that the concentration at the surface remains nearly same but after η = 2 it increases slightly with an increase in the values of n. |
 |
| Case VIII: |
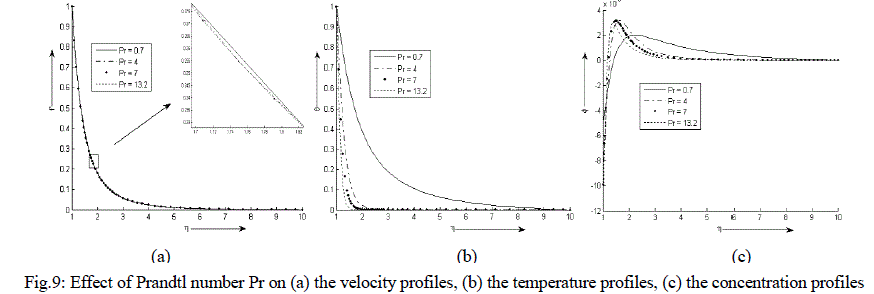
| Figure 9 (a) - (c) exhibit velocity, temperature and concentration profile for various values of Pr. It is observed that the velocity and temperature decreases exponentially from its maximum value at the surface to its minimum value at the end of the boundary layer. The concentration is less near the surface than at the edge of the boundary layer. It increases near the surface, attends its maximum value at about η = 1.5 and η = 2 and then decreases slowly and attains a fix value at the end of the boundary layer. It is also noticed that with an increase in the values of Prandtl number Pr, the velocity decreases negligibly while the temperature of the binary fluid mixture decreases sharply. The concentration increases at and near the surface of the cylinder with an increase in the values of Pr but reverse effect is observed after the attainment of the maximum value. |
 |
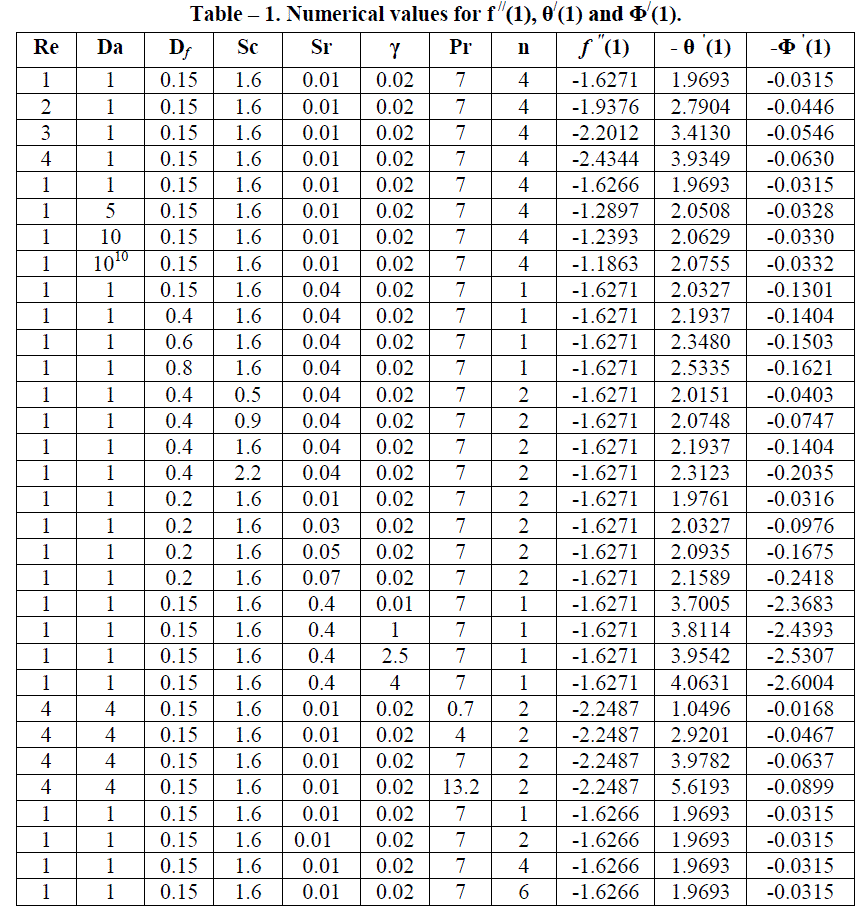
| Finally, the skin friction coefficient, the Nusselt and the Sherwood numbers for the various parameters are shown in Table – 1.The behaviour of these parameters is self – evident from the Table - 1 and hence further discussion about them seems to be redundant. |
 |
V. CONCLUSION |
| The temperature of the binary fluid mixture decreases with the increase of Reynolds, Darcy, Schmidt, Dufour, Soret and Prandtl numbers and order of the chemical reaction whereas increases with the increase of dimensionless chemical reaction parameter. Concentration of the rarer and lighter component of the binary fluid mixture increases to its maximum value and then decreases with the increase of Reynolds, Darcy, Dufour and Prandtl numbers and dimensionless chemical reaction parameter whereas decreases to its maximum value and then increases with the increase of Schmidt and Soret numbers and order of chemical reaction. It is hoped that the present work will serve as a motivation for future experimental work which seems to be lacking at the present time. |
References |
|