ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
1Borkar Pravin Kumar, 2Jha Manoj, 3Qureshi M.F., 4Agrawal G.K.
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, adaptive network based fuzzy inference system (ANFIS) was used in control applications of a Heat Exchanger as interval type-2 fuzzy logic controller (IT-2FL). Two adaptive networks based fuzzy inference systems were chosen to design type-2 fuzzy logic controllers for each control applications. The whole integrated system for control of Heat Exchanger is called IT2 FLC+ANFIS controller. Membership functions in interval type-2 fuzzy logic controllers were set as an area called footprint of uncertainty (FOU), which is limited by two membership functions of adaptive network based fuzzy inference systems; they were upper membership function (UMF) and lower membership function (LMF). This work deals with the design and application of an IT2 FLC+ANFIS controller for a heat exchanger. To deal with the problem of parameter adjustment, efficient neuro-fuzzy scheme known as the ANFIS (Adaptive Network-based Fuzzy Inference System) can be used. The IT2 FLC+ANFIS controller of the heat exchanger is compared with classical PID control. System behaviors were defined by Lagrange formulation and MATLAB computer simulations. The simulation results confirm that interval type2 fuzzy is one of the possibilities for successful control of heat exchangers. The advantage of this approach is that it is not a linear-model-based strategy. Comparison of the simulation results obtained using IT2 FLC+ANFIS controller and those obtained using classical PID control demonstrates the effectiveness and superiority of the proposed approach because of the smaller consumption of the heating medium
Keywords |
| Adaptive network based fuzzy inference system, interval type-2fuzzy controller, Heat Exchanger, control simulation |
INTRODUCTION |
| Fuzzy sets (of type-1) and fuzzy logic are the basis for fuzzy systems, where their objective has been to model how the brain manipulates inexact information. Type-2 fuzzy sets are used to control uncertainty and imprecision in a better way. These type-2 fuzzy sets were originally presented by Zadeh (1975) and are essentially âÃâ¬Ãâ¢fuzzy fuzzyâÃâ¬Ãâ sets, where the fuzzy degree of membership is a type-1 fuzzy set (Zadeh, 1988; Castillo et al 2008). The new concepts were introduced (Liang et al 2000; Mendel, 2001; Adak et al 2011) allowing the characterization of a type-2 fuzzy set with a superior membership function and an inferior membership function; these two functions can be represented, each one by a type-1 fuzzy set membership function. The interval between these two functions represents the footprint of uncertainty (FOU), which is used to characterize a type-2 fuzzy set. While traditionally, type 1 FLCs have been employed widely in nonlinear system‘s control, it has become apparent in recent years that the type-1 FLC cannot fully handle high levels of uncertainties as its MFs (membership functions) are in fact completely crisp (Hagras, 2004; Mendel, 2001; Adak et al 2011). The linguistic and numerical uncertainties associated with dynamic unstructured environments cause problems in determining the exact and precise MFs during the system FLC design. Moreover, the designed type-1 fuzzy sets can be suboptimal under specific environmental and operational conditions. The environmental changes and the associated uncertainties might require the continuous tuning of the type-1 MFs as otherwise; the type-1 FLC performance might deteriorate (Mendel, 2001). As a consequence, research has started to focus on the possibilities of higher order FLCs, such as type-2 FLCs that use type-2 fuzzy sets. A type-2 fuzzy set is characterized by a fuzzy MF, that is, the membership value (or membership grade) for each element of this set is a fuzzy set in [0, 1], unlike a type-1 fuzzy set where the membership grade is a crisp number in [0,1] (Hagras, 2004). The MF of a type-2 fuzzy set is three dimensional and includes a footprint of uncertainty. It is the third dimension of the type-2 fuzzy sets and the footprint of uncertainty that provide additional degrees of freedom making it possible to better model and handle uncertainties as compared to type-1 fuzzy sets. In this paper, adaptive network based fuzzy inference system (ANFIS) was used as interval type-2 fuzzy logic controller (IT-2FL) in control strategies of the Heat Exchanger. Interval type2 fuzzy logic control was not taken into consideration by this approach in most of the cited investigations, despite some of its advantages indicated in this study. Proposed type-2 fuzzy logic controller combines two different control techniques which are adaptive network based fuzzy logic inference system control and interval type-2 fuzzy logic control, and uses their control performances together. Adaptive network based fuzzy inference system (ANFIS) uses a hybrid learning algorithm to identify parameters of Sugeno-type fuzzy inference systems. A combination of the least squares method and the back propagation gradient descent method is used in training interval type2 fuzzy inference system (IT2FIS) membership function parameters to emulate a given training data set. Moreover MATLAB/Sim-Mechanics toolbox and computer aided design program (Solid Works) was used together for visual simulations.. Also MATLAB/ANFIS toolbox was used to create adaptive network based fuzzy logic inference system controllers. |
| The ANFIS is a cross between an artificial neural network and an interval type2 fuzzy inference system (IT2FIS) and represents Takagi-Sugeno fuzzy model as generalized feed forward neural network, and trains it with Heat Exchanger I/O data, thereby adjusting the parameters of the antecedent membership functions as well as those of the functional consequents. A procedure for designing adaptive type-2 FLCs has been developed. An ANFIS (Adaptive Neuro Fuzzy Inference System) technique is used to reduce the computational load of adaptive type-2 FLCs without losing the control efficiency. In fact the use of an ANFIS technique allows to decrease the number of the FLC rules needed to achieve a good control, reducing the computational load, making the controller more flexible and guaranteeing a high performance. |
MATHEMATICAL MODEL OF HEAT EXCHANGER |
| Consider a co-current tubular heat exchanger (VasiÃâÃÂkaninová et al 2010), where petroleum (subscript 1) is heated by hot water (subscript 3) through a copper tube (subscript 2). The controlled variable is the outlet petroleum temperature T1out. Among the input variables, the water flow rate q3(t), is selected as the control variable, whereas the other inlet variables are constant. Parameters and steady-state inputs of the heat exchanger are enumerated in Table 1, where the superscript s denotes the steady state and the subscript in denotes the inlet.` |
| The mathematical model of the heat exchanger is derived under several simplifying assumptions and described by three partial differential equations. |
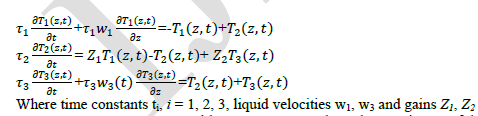 |
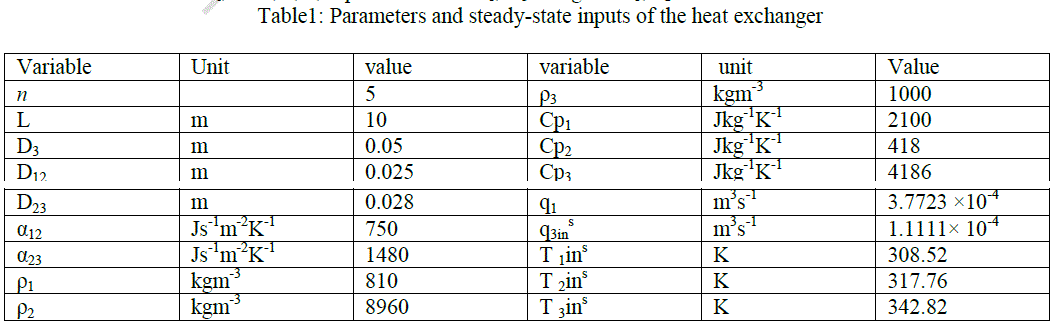 |
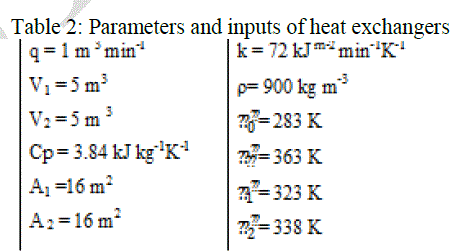 |
| Here, D is the tube diameter, ïÃÂò is the density, C P is the specific heat capacity, α is the heat transfer coefficient, q is the volumetric flow rate. |
INTERVAL TYPE-2 FUZZY DYNAMIC MODEL OF HEAT EXCHANGER |
| Concept of Interval type-2 fuzzy sets |
 |
 |
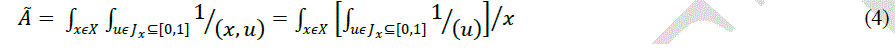 |
| InputsâÃâ¬Ãâ to âÃâ¬Ãâ¢Crisp OutputsâÃâ¬Ãâ), and this mapping can be expressed quantitatively as Y = f (x). This IT2 FLS is finding its way into many engineering applications, and is also known as interval type-2 fuzzy logic controller (IT2 FLC) (Hagras, 2007), interval type -2 fuzzy expert system, or interval type-2 fuzzy model. |
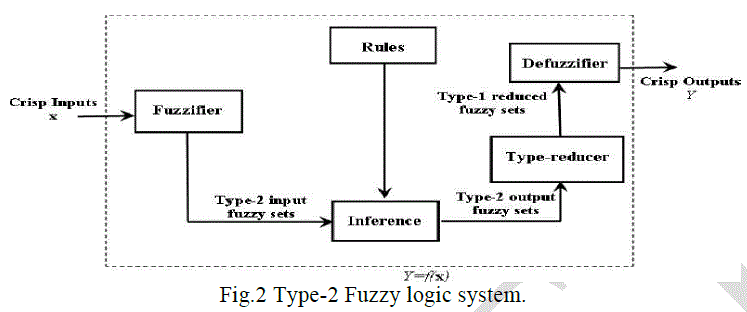 |
| The inputs to the IT2 FLS prior to fuzzification may be certain (e.g., perfect measurements) or uncertain (e.g., noisy measurements). T1 or IT2 FSs can be used to model the latter measurements. The IT2 FLS works as follows: the crisp inputs are first fuzzified into either type -0 (known as singleton fuzzification), type-1 or IT2 FSs, which then activate the inference engine and the rule base to produce output IT2 FSs. These IT2 FSs are then processed by a type-reducer (which combines the output sets and then performs a centroid calculation), leading to an interval T1 FS called the type-reduced set. A defuzzifier then defuzzifies the type-reduced set to produce crisp outputs. Rules are the heart of a FLS, and may be provided by experts or can be extracted from numerical data. In either case, rules can be expressed as a collection of IF– THEN statements. |
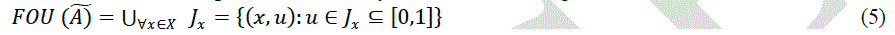 |
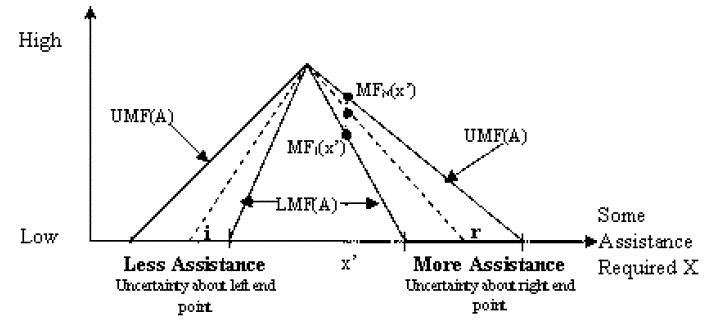
| Where x and y are the inputs, Ai and Bi are the fuzzy sets, fi is the outputs within the fuzzy region specified by the fuzzy rule, pi, qi and ri are the design parameters that are determined during the training process (Widrow et al 1985). The proposed ANFIS model combined the neural network adaptive capabilities and the fuzzy logic qualitative approach (Zadeh, 1989). Intelligent systems based on fuzzy logic are fundamental tools for nonlinear complex system control. Type-2 fuzzy sets are used to control uncertainty and imprecision in a better way. These type-2 fuzzy sets were originally presented by Zadeh (1975) and are essentially âÃâ¬Ãâ¢fuzzy fuzzyâÃâ¬Ãâ sets where the fuzzy degree of membership is a type-1 fuzzy set (Zadeh, 1989). The new concepts were introduced by Liang and Mendel allowing the characterization of a type-2 fuzzy set with a superior membership function and an inferior membership function; these two functions can be represented each one by a type-1 fuzzy set membership function. The interval between these two functions represents the footprint of uncertainty (FOU), which is used to characterize a type 2 fuzzy set shown in Fig.1. Structure of interval type-2 fuzzy logic inference system was given in Fig.2. After all these instructions about ANFIS and interval type-2 fuzzy inference systems, ANFIS controllers were used in control applications, then IT2-FL controllers were built according to performances of ANFIS controllers over the double inverted pendulum, a single flexible link and flexible link carrying pendulum systems. Realization phases of this study were given in Fig.4. |
| Defuzzification process |
| Once the fuzzy controller is activated, the rule evaluation is performed and all the rules which are true are fired. Utilizing the true output membership functions, the defuzzification is then applied to determine a crisp control action. The defuzzification is to transform the control signal into an exact control output. For the Sugeno-style inference, we have to choose between wtaver (weighted average) or wtsum (weighted sum) defuzzification method. In the defuzzification process of the adaptive network based fuzzy logic controller, the method of weighted average (wtaver) is used: |
 |
| The aim of this paper is to model a new approach for interval type-2 fuzzy logic controller by using adaptive network based fuzzy inference system. Three interval type-2 fuzzy logic controllers were designed and used to control the Heat Exchanger. The Heat Exchanger were chosen such as nonlinear systems and they were controlled by proposed IT2-FL controllers to show efficiency of IT2-FL control and verify validity of this new approach. In this study, adaptive networks based fuzzy inference system (ANFIS) controller was designed and applied to Heat Exchanger. ANFIS controller was used for control of Heat Exchanger with interval type-2 membership functions and definite number of rule bases. Moreover this ANFIS controller was combined to create an interval type-2 fuzzy logic controller. Eventually an interval type-2 fuzzy logic controller was obtained for proposed Heat Exchanger by using adaptive network based fuzzy inference system. |
| In this paper, the forward hybrid learning algorithm is used for the neural network part of the ANFIS controller. The continuous interval type-2 fuzzy dynamic model, proposed by (Liang et al 2000) is described by interval type-2 fuzzy if-then rules. It can be seen as a combination of linguistic modeling and mathematical regression, in the sense that the antecedents describe interval type-2 fuzzy regions in the input space in which consequent functions are valid. The ith rule is of the following form (Song-Shyong et al 2007). Plant Rule i: |
 |
| Rule Derivation from Interval Type 2 T-S Fuzzy Model |
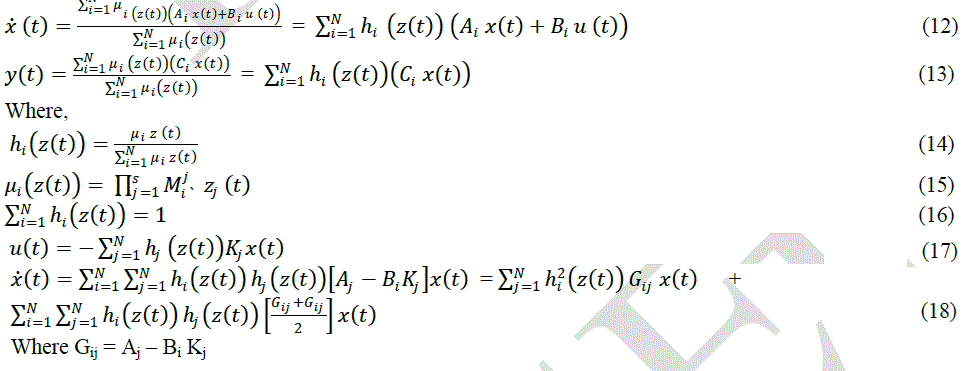 |
DESIGN FRAMEWORK OF THE SYSTEM |
| An independent agent that fuzzifies and normalizes the input parameters for the base ANFIS system is described in this section. Such interactive user interface receives environmental parameters from the users and propagates system‘s decision support to them. The user interface also helps in normalizing the environmental parameters within given range and hence smoothen the operations of the base ANFIS system. The structure of proposed system is described in Fig.3. |
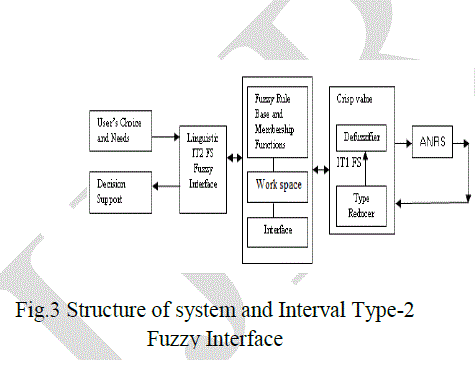 |
| The basic objective of the above architecture is to enable users to enter their choices and requirements in fuzzy form. Since the input is in fuzzy form, there is a need to defuzzify it in crisp normalized values; so as the base ANFIS system process it for decision making. The interface has major components like IT2-FS linguistic interface, a fully rule base, definition of membership functions and inference mechanism. Since IT2-FS maps fuzzy to fuzzy, there is requirement of type reducing facility, which reduces the resulting fuzzy values from the T2-FS into crisp values with the help of IT1FS defuzzifier. The work space can be used to hold temporary results during inference and conversion. |
| ANFIS |
| A Takagi-Sugeno (1985) fuzzy system may be presented in the form of a neural network structure. This form is called ANFIS (Adaptive Neuro Fuzzy Inference System)(Jang, 1993). The main advantage of the ANFIS technique is the construction of an input-output mapping based on both human knowledge (in the form of fuzzy if-then rules) and stipulated input-output data pairs.Type-2 fuzzy controller optimization |
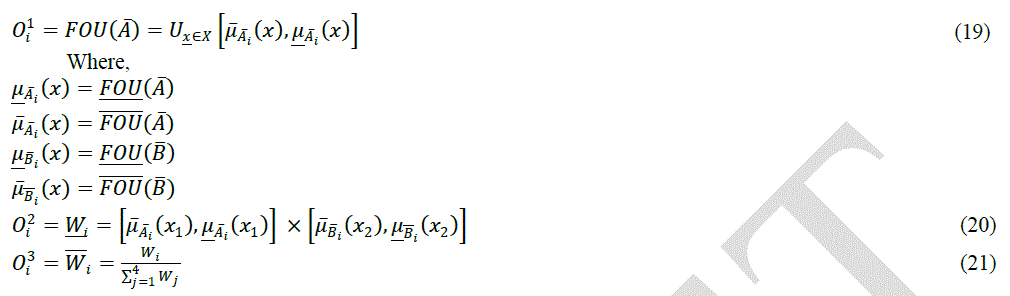 |
| Rule Reduction Technique using Adaptive interval type-2 fuzzy logic controller |
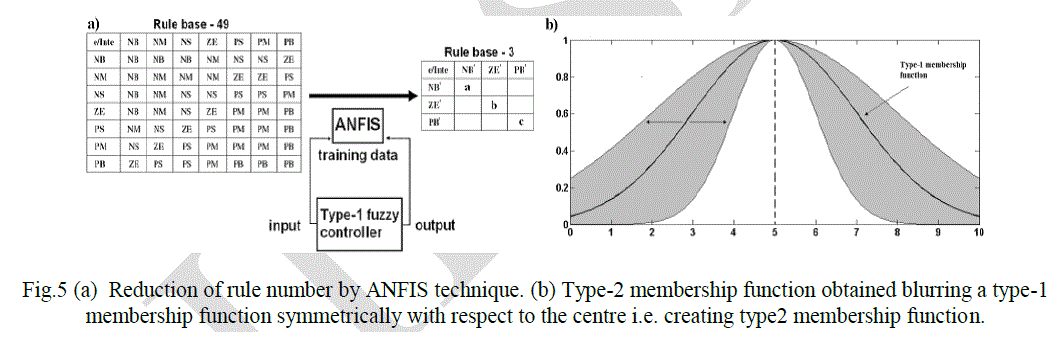
| The use of a large number of rules in a fuzzy logic controller makes the control system more accurate and precise, providing a high performance, but increases the computational load of the processor. The reduction of the rule number of adaptive interval type-2 fuzzy controllers is possible through the ANFIS optimization technique that uses as inputs a type-1 fuzzy controller with a large number of rules and the error and the integral of the error. In the proposed optimization method, the inputs and the outputs of a type-1 fuzzy controller with a 49 rule base constitute the training data for the adaptive network-based fuzzy inference system (ANFIS). The training paradigm uses a gradient descent and a least squares algorithm to optimize the antecedent and the consequent parameters respectively. |
 |
| The procedure to tune the type-2 fuzzy controller starts with type-1 fuzzy sets because it is not possible to apply the ANFIS directly to a type-2 fuzzy system (Mendel, 2001). The new optimized type-1 fuzzy system obtained with ANFIS is therefore used to initialize the parameters of the new type-2 fuzzy system. The center of type-2 Gaussian membership functions is the same of that of type-1 Gaussian membership functions, while the amplitude values for the external (upper) and internal (lower) membership functions of type-2 fuzzy sets are instead chosen minimizing the integral of absolute error (iae). In addition each amplitude value of a type-1 fuzzy Gaussian membership function is the average of the amplitude values of the lower and upper type-2 fuzzy Gaussian membership functions (Fig. 5b). This new optimized type-2 fuzzy system, with first order Sugeno inference, constitutes the new type-2 fuzzy controller with only 3 rules. |
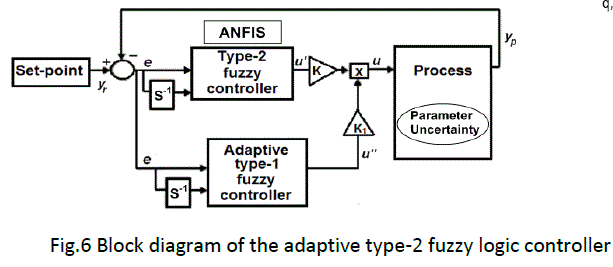
| The adaptive interval type-2 fuzzy logic controller (AIT2FLC) has a structure similar to the controller proposed by ( Mudi et al 2000). |
| The control variable generated by the type-2 fuzzy logic controller u‘(t) multiplied by the scaling factor K is updated, with the product operator, by the signal that comes from the adaptive type-1 fuzzy controller K1u‘‘. The resulting signal u(t) is then sent to the plant, characterized by time-variant parameters Fig. 6. The error (e) and the integral of the error (int e) are, also in this case, the inputs of the two fuzzy controllers (the main and the adaptive). |
 |
SIMULATIONS AND RESULTS |
| Shell Heat Exchangers |
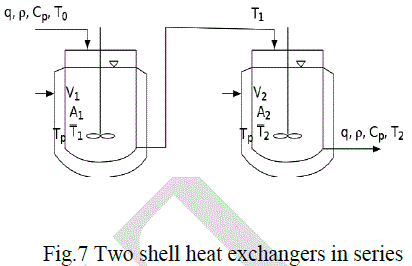
| Consider two heat exchangers shown in Fig.7. The measured and controlled output is temperature from second exchanger. The control objective is to keep the temperature of the output stream close to a desired value 343 K. The control signal is input volumetric flow rate of the heated liquid. Assume ideal liquid mixing and zero heat losses. We neglect accumulation ability of exchanger‘s walls. Hold-ups of exchanger as well as flow rates and liquid specific heat capacity are constant. |
| Under these assumptions the mathematical model of the exchangers is given as |
 |
| Simulation results obtained using designed IT2 FLC+ANFIS controller and two PID controllers are shown in Fig.8 & Fig.9. Fig.10 compares controlled outputs in the task of set point tracking. The set point changes from 312.32 K to 310.32 K at time 190 s and then to 313.55 K at time 380 s. The comparison of the controller outputs is shown in Fig.9; Fig.10 presents the simulation results of the IT2 FLC+ANFIS controller and PID control of the heat exchanger in the task of disturbance rejection. Disturbances were represented by inlet water temperature changes from 344.25 K to 340.25 K at time 190 s, from 340.25 K to 349.25 K at time 580 s and to 344.25 K at time 990 s. The comparison of the controller outputs is shown in Fig.11. The energy consumption is measured by the total amount of hot water consumed during the control process. The situation for IT2 FLC+ANFIS controller and PID controllers is presented in Figs.12 &, Fig.13 and it can be stated that the smallest energy consumption is assured using IT2 FLC+ANFIS controller. The results obtained by PID controllers are practically identical. The control response obtained by IT2 FLC+ANFIS controller is the best one; it has the smallest overshoots and the shortest settling times. The simulation results were compared also using integral quality criteria ise (integrated squared error) and iae (integrated absolute error) (Ogunnaike and Ray, 1994). The results are compared in Table 3. |
 |
DISCUSSION |
| The comparison of the two types of controllers (IT2 FS+ANFIS & PDI) was made using iae and ise criteria described below: |
 |
 |
| The disadvantage of the PID controllers is that using these controllers can lead to nonzero steady-state errors, but without overshoots and undershoots practically. In the case of the (IT2 FS+ANFIS controller with integrator using steady-state control error is equal zero but the control responses show any overshoots and undershoots. |
 |
CONCLUSIONS |
| Simulation results confirm the superiority of the IT2 FS+ANFIS control, over the simple PID controllers, in obtaining a high speed response and a limited offset, thanks to a slender, but equally efficient, rule set obtained with the ANFIS technique. The union of the ANFIS optimization method and the adaptive fuzzy algorithm operating on the output scaling factor, allows to obtain a IT2 FS+ANFIS control able to minimize all the negative effects of parameter changes (step or ramp disturbances) achieving a very high control performance with a minimum computational load. In this paper, a stable nonlinear IT2 FS+ANFIS controller based on parallel distributed fuzzy controllers is proposed. Each sub-controller is IT2 FS+ANFIS designed and provides local optimal solution. The Takagi-Sugeno fuzzy model is employed to approximate the nonlinear model of the controlled Heat Exchanger. Based on the IT2 FS+ANFIS model, a IT2 FS+ANFIS controller is developed to guarantee not only the stability of neuro-fuzzy model and neuro-fuzzy control system for the heat exchanger but also control the transient behavior of the system. The design procedure is conceptually simple and natural. Therefore, they can be solved very efficiently in practice by IT2 FS+ANFIS control technique. Simulation results shows that the IT2 FS+ANFIS control approach is robust and exhibits a superior performance to that of established traditional PID control methods. Comparison of the IT2 FS+ANFIS simulation results with classical PID controls demonstrates the effectiveness and superiority of the proposed approach. |
References |
|