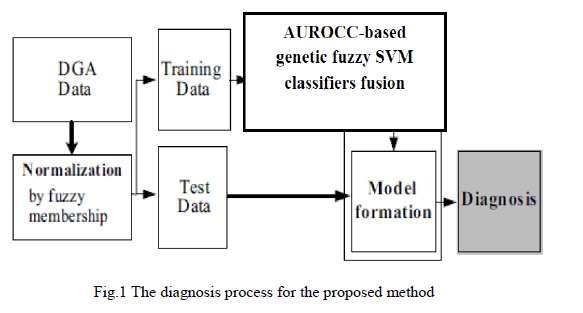
ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
P.Raju1 and G.Muralidharan2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A Bipedal robots have been considered as the best means of locomotion on any irregular surfaces. But achieving stability of the robot during walking is difficult. Several studies have been proposed for achieving stability. This paper discusses the overview of various approaches that have been designed so far for achieving stability during walking. The main objective of this paper is to construct a bipedal robot with height sensor at the foot to measure the robot position coordinates. In order to make a stable walk, the position vector coordinates has to be calculated. The position vector coordinate is computed by Denavit Hartenberg representation and inverse kinematics. The DH representation is used to find the coordinates relative to the joint angles of the robot. The measured coordinates are then used to control the joint angle that controls the robot walking. This paper also discusses about the force torque controlled actuation of the joint motor of the robot during walking on uneven and non-linear surfaces. The torso is designed to make the robot walking upright by itself. The trajectory of the robot can be identified by placing the height sensor at the robot foot. This sensor reads the Z axis value as the robot is walking on the floor. By using this measured Z axis and known X axis values, the robot predicts its path and manipulates its trajectory by itself. The biped robot stability can be controlled by constantly shifting the center of gravity (COG) to the right and left leg of the robot during walking. The camera is placed at the hip to maneuver the obstacles along the path. The Mathematical modelling of the biped robot is done to find the torque acting at the joints. The computed point (position vector of the foot) coordinates along the trajectory is then proved through the simulation using MATLAB/Simulink.
Keywords |
| Biped robot, Mathematical modelling, MATLAB/Simulink, Passive dynamic walking, DH Representation |
INTRODUCTION |
| Various approaches have been proposed to make the robot walking dynamically. Of them, zero moment point (ZMP) method is extensively used in these areas. The ZMP method is assumed that the robot had flat feet provided during walking. The passive dynamic walking is achieved only when an inverted pendulum approach were used. The human inspired walking robot is mimicked like the humans actuate the joints to realize walking. The methods proposed so far are difficult to understand. But this paper will present an easy way of computing the robot leg position coordinates. The force torque relationship of the rigid link of the robot is stated briefly in this paper. This kind of unique way is very much needed to actuate the joints according to the force experienced by the leg when it touches the ground. This force is often called as the ground reaction forces. The analysis of the ground reaction force distribution is very important for determining the robotâÃâ¬ÃŸs stability. Analyzing the force exerted by robotâÃâ¬ÃŸs leg on the ground is important for the synthesis of position control. As it is already mentioned, the main objective of this paper is to construct a bipedal robot with torso for balanced walking. The torso control dynamically changes the position of center of gravity from one foot to another during dynamic walking. The mechanical design of the robot and its degrees of freedom (DOF) are clearly explained in section II. The mathematical modelling of the biped robot is explained in section III. Section IV gives the trajectory information for the robot with the help of sensor at the foot to maintain the balance of the biped robot. |
MECHANICAL DESIGN |
| The most important considerations in mechanical design are that the robot should have sufficient degrees of freedom to balance and walk dynamically. The link of the robot must be rigid to withstand the pressure and the forces exerted on them. A bipedal robot suitable for dynamic walking requires robust force torque control to actuate the links for locomotion. |
| A. DOF of the robot |
| The bipedal robot at least requires 2 DOF to move its leg. A human leg has more than 30 DOF to attain a perfect locomotion. Higher the DOF, higher the complexity arises in the robot. So, for the sake of simplicity in analysis, the biped robot with fewer DOF has proposed. The biped structure proposed in this paper has 11 DOF, in which HIP and ANKLE possess 2 DOF each in pitch and Yaw axis. The anthropomorphic knee possesses 1 DOF and the active torso joint has 1 DOF. |
| B. Torso control |
| A torso design provides the ability to move around, gives support and structure to the robotâÃâ¬ÃŸs body during walking. The torso plays a vital role in changing the COG to the stance leg during walking. A stance leg is nothing but the leg that touches with the ground. A yaw movement is provided to the torso to shift the COG in order to maintain a stable walk. A torso is an active joint with 1 DOF and an actuated through a yaw motion. Figure 2.1 shows the CAD model of the robot designed in Pro- Engineer. |
 |
| A. Ankle joint |
| Figure 2.2 shows the structure of ankle joint of the robot. The structure has rubber type foot sole and several foot sensors used for force-torque optimization. The sensor placed at the foot measures the ground reaction forces exerted by the robot during walking. The foot sole made of rubber will reduce the impact at the joint during landing. |
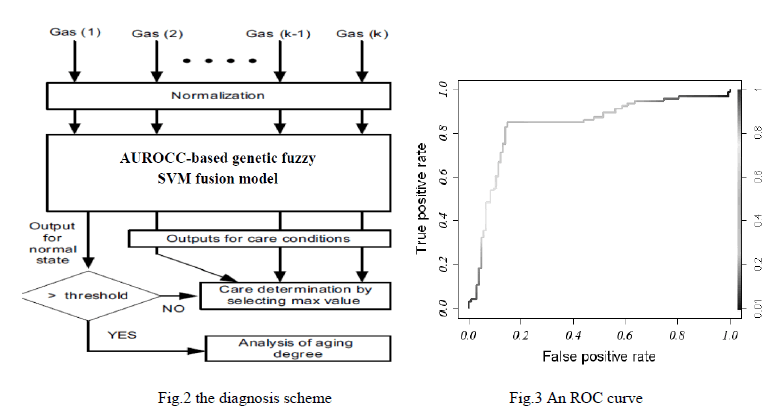 |
KINEMATIC MODELLING |
| The kinematics is the study of the robot's movements with regard to a reference system. The kinematics model is used to find the robotâÃâ¬ÃŸs position and the orientation of the foot and the values of their joint coordinate. Figure (3.1) shows the block diagram of the modelling procedure of the biped robot. |
| A. Modelling of biped robot |
| The following considerations are defined to model the biped robot. |
| • First define the coordinate system of the biped robot. |
| • Set the reference coordinates as the origin to describe the location of the other joints indirectly. |
| • Use DH parameters to calculate the position vector and orientation matrix. |
| • Imply inverse kinematics to calculate the joint angles by fixing the position coordinate vector. |
| • Find the different joint angles for different feet position coordinates along the trajectory of the robot. |
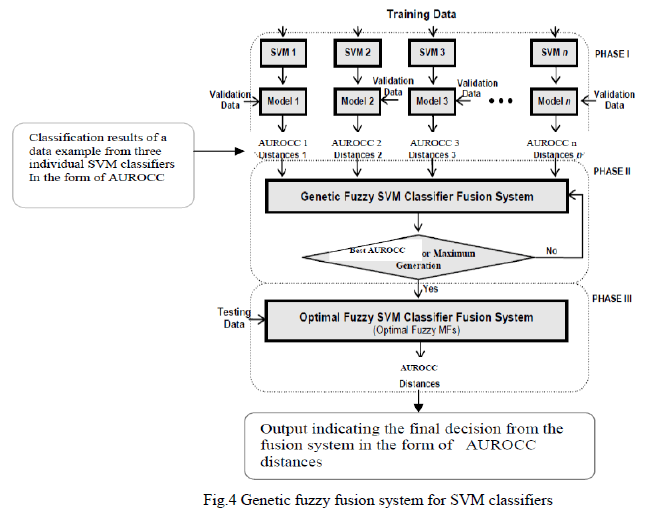 |
| B. Kinematics representation |
| The kinematic model of a robot can be represented by the homogeneous transformation matrix. This representation is necessary for robots with more than two degrees of freedom. A robot of n degrees of freedom (DOF) is formed by n links assembled by n articulations, in such way that each articulation-link constitutes a DOF. When homogeneous transformation matrix is used to represent the position and the relative orientation between two consequent links, a reference system to each link must be associated. Thus, it is possible to represent the translations and relative rotations between the different links. Where the matrix Ln+1 represents the position and relative orientation between the associated systems of two consequent robot's links. This matrix allows a total or partial representation of the robot's kinematics. |
| For example, 0L1 represents the position and orientation of the first link relative to the base reference, and 0L3 = 0L1 1L2 2L3 represents the position and orientation of the third link relative to the base reference coordinate system. When the DOF are considered, the nLn+1 matrix have to be found out. Thus, for six degrees of freedom robot per leg, the final links position and orientation is represented by the R matrix: |
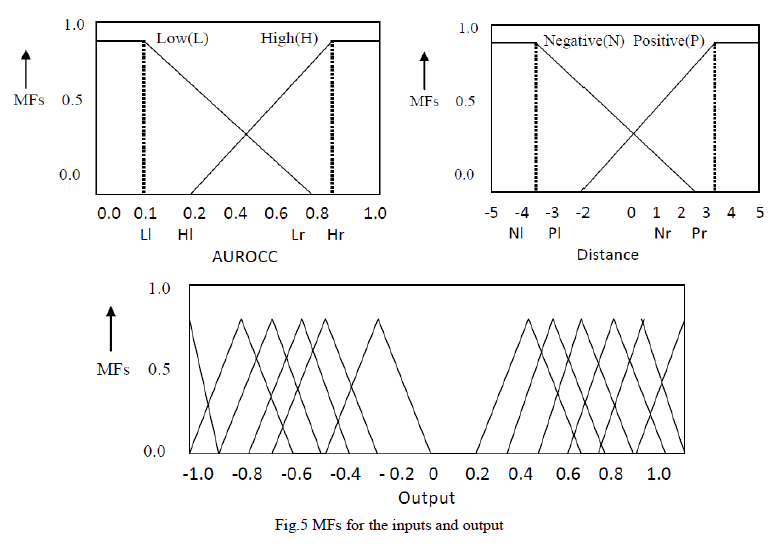 |
| In order to locate the coordinate systems from each link and to obtain the robot's kinematics, Denavit-Hartenberg (D-H) method is used. D-H methods describe robotâÃâ¬ÃŸs kinematics and represent its motions. It has four parameters namely {α, θ, d and a}. These parameters are used to find the joint angles of the robot link. Figure (3.2) represents the robot joints and its angles rotation with respect to the base frame. The base frame assumed is as shown in the figure (3.3). The twist angle of the robot links can be found out by comparing the joints rotation relative to the base frame. If it rotates in clockwise direction relative to the axis assumed in base frame, the twist angle “α” should be taken as -90Ãâ¹ÃÅ¡ and if it rotates in counter clockwise direction, the twist angle assumed is 90Ãâ¹ÃÅ¡. |
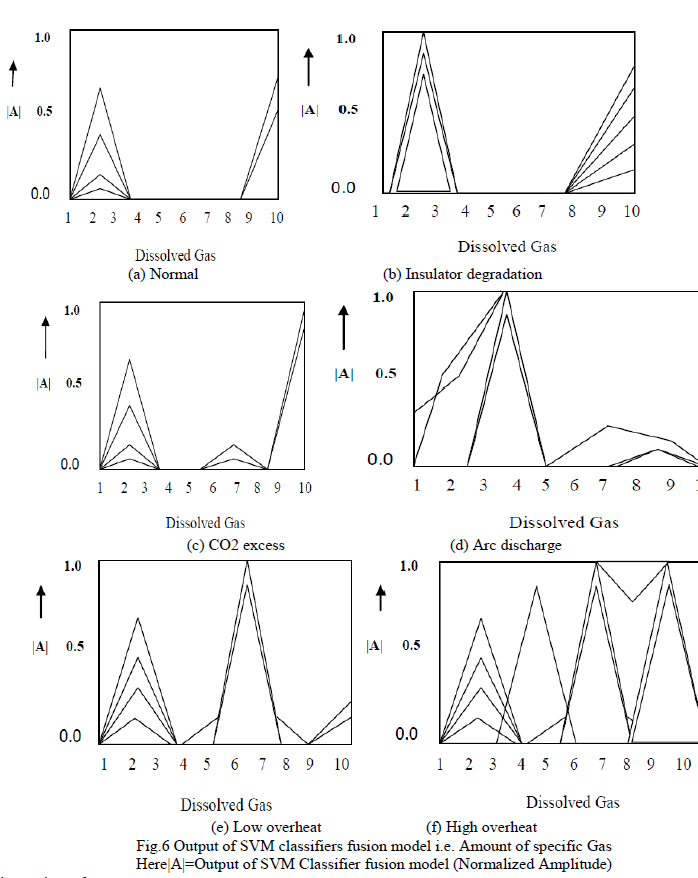 |
| A. DH Matrix |
| After getting all the parameters as in the table 3.1, the Position coordinates, orientation and rotation of the biped robot relative to the base frame is calculated by substituting the value in equation (). |
| The DH matrix is |
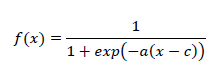 |
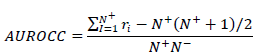 |
| B. Torque calculation |
| In order to achieve stability, the rotation of the joint angles must be controlled properly. It can be obtained by calculating the amount of torque required to actuate the joint motor of the biped robot during walking. |
| Figure (3.3) shows the torque parameters of the biped robot ankle. The torque calculation is done when the robot is in double support phase, i.e., both the leg of the robot touches with the ground. |
| a. Torque at the ankle |
| To find the torque at the ankle, some assumptions has to be made. The link between the hip, foot and knee are massless and the angle between the foot and ground is zero. The maximum torque at the ankle is calculated when the entire weight of the robot acting on the edge of the robot foot except the grounded foot. |
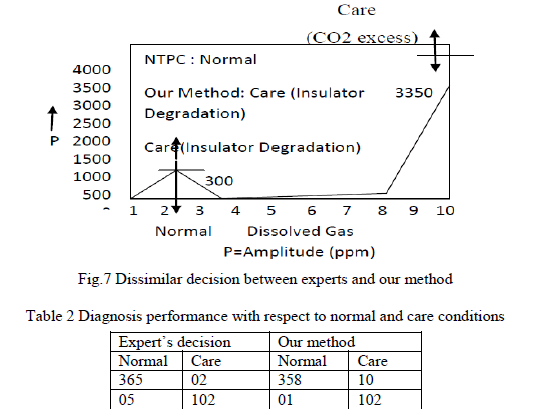 |
| c. Torque at the hip joint |
 |
TRAJECTORY GENERATION |
| The sensor fixed at the foot measures the z axis height when the leg moving from standing phase to swinging phase. In between the phases, a lot of intermediate points are considered. Each point can be determined through the height sensor fixed at the robot leg. This value can then be substituted with the DH representation position vector equation Px, Py, Pz to obtain the torques acting at the joints. These torque (θ1, θ2) can be found from the equations (2),(3),(4) as described in chapter III. |
| The height sensor fixed at the robot foot measures the Pz values for different set of points from one position to other (Z0-Z1) as shown in the figure 4.1. As, it is already mentioned the value for Px is step length and is constant. If the step length (Px) varies, the number of steps robot takes to reach from one position to other is also varied. In this project, the step length (Px) is fixed value. It cannot be changed during the walking of the biped robot. Figure 4.1 shows the trajectory information and the set of points are obtained from the sensor |
 |
| The camera placed at the hip senses the obstacles present along the path and sends the information to the joint motor again to move in proper directions. After calculating those points, the inverse kinematics is done and the position coordinates are found out. These coordinates are then used to find angle required to actuate the joint motors by taking the inverse kinematics. In this way, the biped robot intelligently identifies the trajectories and the robot path is planned by itself. The ground surface of the robot is modelled as a set of (x, z) points. Here the x value (step length) is kept constant. Step length is nothing but the amount of distance between each steps of the robot during walking. The „zâÃâ¬ÃŸ axis values are obtained from the height sensor and hence the trajectory is generated and the robot is controlled. |
CONCLUSION |
| The intelligent path planning biped robot with 10 DOF is constructed and its mechanism, stability, torque calculation are found out. The height measuring sensor was used at the robot foot to generate the path by the robot itself. The camera placed at the hip of the biped robot senses the obstacles on the path and notifies the controller to turn to other directions. This made it an intelligent path planning biped robot. In order to withstand the forces exerted on the links, the high quality aluminum channel can be used for making rigid structure. |
| For further improvement, the camera has to be placed at the foot for the trajectory generation instead of the sensor. The camera controls the robot as well as predicting the path through 3D calibration technique. By adopting the camera based trajectory generation, the biped robot can be efficiently controlled with greater stability. |
References |
|