ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Sandeep Singh Dept. of Mathematics, D. A. V. College, Chandigarh, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, we present scond -order Jarrat method for computing zeros of system of nonlinear equations numerically. In this paper, we extending the idea of the proposed families of Jarrat method to system of nonlinear equations .It is proved that the above said families have second order of convergence. Several numerical examples are also given to illustrate the efficiency and the performance of the presented families.
Keywords |
| System of Nonlinear equations, Optimal Order of Convergence, Halley's method, Schroder's method, Jarrat method. |
INTRODUCTION |
| Due to the fact that systems of nonlinear equations arise frequently in science and engineering they have attracted researcher's interest. For example, nonlinear systems of equations, after the necessary processing step of implicit discretization, are solved by finding the solutions of systems of equations. We consider here the problem of finding a real zero, x*= (x*1, x*2…….; x*n)T, of a system of non linear equations |
 |
 |
 |
NUMERICAL RESULTS |
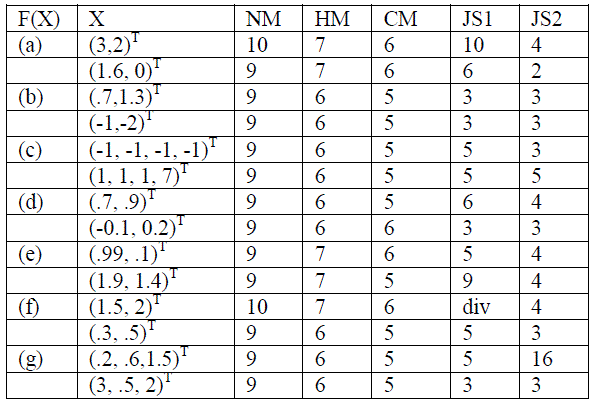
| In this section, we shall check the performance of the present formula JS1(2:15) and JS2(2:16) the comparison is carried out with Newton's method and with HM and CM [8]. A mat lab program has been written to implement these methods. We use the following stopping criteria for computer programs: |
| For every method, we analyze the number of iterations needed to converge to the required solution. The numerical results are reported in the Table 1. |
| We consider the following problems for a system of nonlinear equations. |
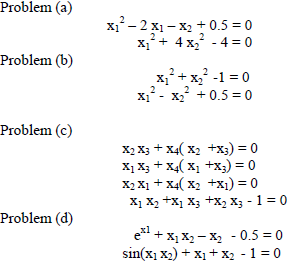 |
 |
 |
CONCLUSIONS |
| The presented formula (2.15) and (2.16) is simple to understand, easy to program and has the second order of convergence. We contribute to the development of iteration processes and propose of Jarratt’s method. We now obtain a wide general class of Jarratt’s methods which are without memory and have the same scaling factor of function as that Jarratt's method. Numerical tests have been performed, which not only illustrate the method practically but also serve to check the validity of theoretical results we have derived. The performance is compared with Newton method, CM [8] and HM [8]. |
References |
|